Obsah
1. Rozpoznávání obrázků s knihovnou scikit-learn
2. Rozpoznání ručně napsaných číslic
3. Datová sada obsahující naskenované ručně napsané číslice
4. Metadata a očekávané výsledky z datové sady Digits
5. Přečtení a následné vyobrazení jednotlivých ručně nakreslených číslic
6. Rozpoznání číslic modelem provádějícím logistickou regresi
7. Výsledky rozpoznání číslic modelem logistické regrese
8. Využití modelu SVM (metoda podpůrných vektorů) pro klasifikaci obrázků
9. Výsledky rozpoznání číslic metodou podpůrných vektorů
10. Využití modelu pro hledání K nejbližších sousedů
11. Výsledky rozpoznání číslic modelem hledajícím K nejbližších sousedů
12. Rozpoznání rastrových obrázků neuronovou sítí
13. Výsledky rozpoznání číslic neuronovou sítí
14. Zobrazení původních obrázků i predikovaných výsledků ve vizuální podobě
15. Zobrazení těch číslic, u nichž se model spletl
16. Graf s číslicemi, které nebyly správně rozeznány
17. Zobrazení číslic, které nebyly korektně rozeznány neuronovou sítí
18. Číslice, které nebyly rozpoznány neuronovou sítí
19. Repositář s demonstračními příklady
1. Rozpoznávání obrázků s knihovnou scikit-learn
V dnešním pokračování seriálu o knihovně scikit-learn si ukážeme jeden ze způsobů rozpoznání rastrových obrázků. Použijeme přitom obrázky s velmi malým rozlišením 8×8 pixelů, které lze reprezentovat vektorem s 64 prvky. A takto relativně malé vektory je možné použít pro trénink různých typů modelů – od modelu logistické regrese až po sofistikovanou neuronovou síť. Ovšem současně se nám také ukazují limity tohoto způsobu práce s modely, protože zpracování rastrových dat je dosti specifické – dochází totiž k posunům, popř. rotacím, což ve výsledku vede k tomu, že se modely (i když dobře natrénované) mohou při rozpoznávání obrázků mýlit.
2. Rozpoznání ručně napsaných číslic
Úkol, který budeme dnes řešit, je následující: máme k dispozici sadu obrázků s rozlišením 8×8 pixelů, na nichž jsou ručně napsané číslice, někdy čitelně, jindy dost nečitelně. Našim úkolem bude natrénovat vhodný model s vhodně nastavenými hyperparametry tak, aby dokázal rozpoznat číslici. Bude se tedy jednat o model provádějící klasifikaci, jehož výsledkem je symbol 0, 1, 2, … 9. Vstupní matice X bude obsahovat N vektorů s 64 prvky (což je „zploštělá“ matice 8×8 pixelů) a vstupní vektor y bude obsahovat hodnoty 0, 1, 2… odpovídající rastrovému obrázku číslice reprezentovaného oněmi 64prvkovými vektory.
V knihovně scikit-learn máme k dispozici datovou sadu s naskenovanými číslicemi, která vznikla z databáze MNIST. Dnes použijeme tuto sadu, příště však již budeme rozpoznávat odlišné objekty na obrázcích z databáze CIFAR.
3. Datová sada obsahující naskenované ručně napsané číslice
Víme již, že trénovací i testovací (či verifikační) sada s ručně nakreslenými a naskenovanými číslicemi je přímo součástí balíčku Scikit-learn. Načíst ji můžeme funkcí load_digits z podbalíčku sklearn.datasets, což je koncept, který již velmi dobře známe z dalších datových sad, tedy konkrétně z datové sady Iris a California Housings. Hodnotou, kterou po načtení získáme, je datová struktura s metadaty, vektory s obrázkem (viz další text), maticemi představujícími obrázky, i vektorem s očekávanými číslicemi. V dalším skriptu si ukážeme, jakým způsobem je možné některá vrácená metadata a data zpracovat:
#!/usr/bin/env python
# import funkce, která vrátí obrázky pro práci
from sklearn.datasets import load_digits
# načtení obrázků, s nimiž budeme dále pracovat
digits_data = load_digits()
# zjištění základních informací o obrázcích
print("Description:", digits_data.DESCR)
print("Data:", digits_data.data.shape)
print("Obrázky:", digits_data.images.shape)
# výpis informací o obrázcích
for i in range(0, 10):
print(f"Image #{i}:")
print("Data:\n", digits_data.data[i])
print("Image:\n", digits_data.images[i])
print("Target:\n", digits_data.target[i])
print()
# finito
Nejprve si tímto skriptem necháme zobrazit popis dat a metadat – což jsou informace obsažené v atributu DESCR:
Description: .. _digits_dataset:
Optical recognition of handwritten digits dataset
--------------------------------------------------
**Data Set Characteristics:**
:Number of Instances: 1797
:Number of Attributes: 64
:Attribute Information: 8x8 image of integer pixels in the range 0..16.
:Missing Attribute Values: None
:Creator: E. Alpaydin (alpaydin '@' boun.edu.tr)
:Date: July; 1998
This is a copy of the test set of the UCI ML hand-written digits datasets
https://archive.ics.uci.edu/ml/datasets/Optical+Recognition+of+Handwritten+Digits
The data set contains images of hand-written digits: 10 classes where
each class refers to a digit.
Preprocessing programs made available by NIST were used to extract
normalized bitmaps of handwritten digits from a preprinted form. From a
total of 43 people, 30 contributed to the training set and different 13
to the test set. 32x32 bitmaps are divided into nonoverlapping blocks of
4x4 and the number of on pixels are counted in each block. This generates
an input matrix of 8x8 where each element is an integer in the range
0..16. This reduces dimensionality and gives invariance to small
distortions.
For info on NIST preprocessing routines, see M. D. Garris, J. L. Blue, G.
T. Candela, D. L. Dimmick, J. Geist, P. J. Grother, S. A. Janet, and C.
L. Wilson, NIST Form-Based Handprint Recognition System, NISTIR 5469,
1994.
|details-start|
**References**
|details-split|
- C. Kaynak (1995) Methods of Combining Multiple Classifiers and Their
Applications to Handwritten Digit Recognition, MSc Thesis, Institute of
Graduate Studies in Science and Engineering, Bogazici University.
- E. Alpaydin, C. Kaynak (1998) Cascading Classifiers, Kybernetika.
- Ken Tang and Ponnuthurai N. Suganthan and Xi Yao and A. Kai Qin.
Linear dimensionalityreduction using relevance weighted LDA. School of
Electrical and Electronic Engineering Nanyang Technological University.
2005.
- Claudio Gentile. A New Approximate Maximal Margin Classification
Algorithm. NIPS. 2000.
|details-end|
V rámci dalšího kroku jsou zobrazeny rozměry (resp. přesněji řečeno tvary) n-rozměrných polí uložených v atributech nazvaných data a images:
Data: (1797, 64) Obrázky: (1797, 8, 8)
Ze zobrazených zpráv vidíme, že se vlastně (jedna z možných interpretací) jedná o 1797 64prvkových vektorů, resp. o 1797 dvourozměrných matic 8×8 prvků, což je ve skutečnosti jen odlišný pohled na ony 64prvkové vektory (modely budeme učit na jednorozměrných vektorech, pro zobrazení obrázků naopak použijeme dvourozměrné matice).
Dále si skriptem necháme zobrazit prvních 10 vektorů i prvních 10 dvourozměrných matic:
Image #0: Data: [ 0. 0. 5. 13. 9. 1. 0. 0. 0. 0. 13. 15. 10. 15. 5. 0. 0. 3. 15. 2. 0. 11. 8. 0. 0. 4. 12. 0. 0. 8. 8. 0. 0. 5. 8. 0. 0. 9. 8. 0. 0. 4. 11. 0. 1. 12. 7. 0. 0. 2. 14. 5. 10. 12. 0. 0. 0. 0. 6. 13. 10. 0. 0. 0.] Image: [[ 0. 0. 5. 13. 9. 1. 0. 0.] [ 0. 0. 13. 15. 10. 15. 5. 0.] [ 0. 3. 15. 2. 0. 11. 8. 0.] [ 0. 4. 12. 0. 0. 8. 8. 0.] [ 0. 5. 8. 0. 0. 9. 8. 0.] [ 0. 4. 11. 0. 1. 12. 7. 0.] [ 0. 2. 14. 5. 10. 12. 0. 0.] [ 0. 0. 6. 13. 10. 0. 0. 0.]] Target: 0 Image #1: Data: [ 0. 0. 0. 12. 13. 5. 0. 0. 0. 0. 0. 11. 16. 9. 0. 0. 0. 0. 3. 15. 16. 6. 0. 0. 0. 7. 15. 16. 16. 2. 0. 0. 0. 0. 1. 16. 16. 3. 0. 0. 0. 0. 1. 16. 16. 6. 0. 0. 0. 0. 1. 16. 16. 6. 0. 0. 0. 0. 0. 11. 16. 10. 0. 0.] Image: [[ 0. 0. 0. 12. 13. 5. 0. 0.] [ 0. 0. 0. 11. 16. 9. 0. 0.] [ 0. 0. 3. 15. 16. 6. 0. 0.] [ 0. 7. 15. 16. 16. 2. 0. 0.] [ 0. 0. 1. 16. 16. 3. 0. 0.] [ 0. 0. 1. 16. 16. 6. 0. 0.] [ 0. 0. 1. 16. 16. 6. 0. 0.] [ 0. 0. 0. 11. 16. 10. 0. 0.]] Target: 1 Image #2: Data: [ 0. 0. 0. 4. 15. 12. 0. 0. 0. 0. 3. 16. 15. 14. 0. 0. 0. 0. 8. 13. 8. 16. 0. 0. 0. 0. 1. 6. 15. 11. 0. 0. 0. 1. 8. 13. 15. 1. 0. 0. 0. 9. 16. 16. 5. 0. 0. 0. 0. 3. 13. 16. 16. 11. 5. 0. 0. 0. 0. 3. 11. 16. 9. 0.] Image: [[ 0. 0. 0. 4. 15. 12. 0. 0.] [ 0. 0. 3. 16. 15. 14. 0. 0.] [ 0. 0. 8. 13. 8. 16. 0. 0.] [ 0. 0. 1. 6. 15. 11. 0. 0.] [ 0. 1. 8. 13. 15. 1. 0. 0.] [ 0. 9. 16. 16. 5. 0. 0. 0.] [ 0. 3. 13. 16. 16. 11. 5. 0.] [ 0. 0. 0. 3. 11. 16. 9. 0.]] Target: 2 ... ... ... Image #8: Data: [ 0. 0. 9. 14. 8. 1. 0. 0. 0. 0. 12. 14. 14. 12. 0. 0. 0. 0. 9. 10. 0. 15. 4. 0. 0. 0. 3. 16. 12. 14. 2. 0. 0. 0. 4. 16. 16. 2. 0. 0. 0. 3. 16. 8. 10. 13. 2. 0. 0. 1. 15. 1. 3. 16. 8. 0. 0. 0. 11. 16. 15. 11. 1. 0.] Image: [[ 0. 0. 9. 14. 8. 1. 0. 0.] [ 0. 0. 12. 14. 14. 12. 0. 0.] [ 0. 0. 9. 10. 0. 15. 4. 0.] [ 0. 0. 3. 16. 12. 14. 2. 0.] [ 0. 0. 4. 16. 16. 2. 0. 0.] [ 0. 3. 16. 8. 10. 13. 2. 0.] [ 0. 1. 15. 1. 3. 16. 8. 0.] [ 0. 0. 11. 16. 15. 11. 1. 0.]] Target: 8 Image #9: Data: [ 0. 0. 11. 12. 0. 0. 0. 0. 0. 2. 16. 16. 16. 13. 0. 0. 0. 3. 16. 12. 10. 14. 0. 0. 0. 1. 16. 1. 12. 15. 0. 0. 0. 0. 13. 16. 9. 15. 2. 0. 0. 0. 0. 3. 0. 9. 11. 0. 0. 0. 0. 0. 9. 15. 4. 0. 0. 0. 9. 12. 13. 3. 0. 0.] Image: [[ 0. 0. 11. 12. 0. 0. 0. 0.] [ 0. 2. 16. 16. 16. 13. 0. 0.] [ 0. 3. 16. 12. 10. 14. 0. 0.] [ 0. 1. 16. 1. 12. 15. 0. 0.] [ 0. 0. 13. 16. 9. 15. 2. 0.] [ 0. 0. 0. 3. 0. 9. 11. 0.] [ 0. 0. 0. 0. 9. 15. 4. 0.] [ 0. 0. 9. 12. 13. 3. 0. 0.]] Target: 9
Ve výpisu skriptu se objevuje i atribut nazvaný target. Je to výsledná hodnota, na kterou by měl být natrénován model. Opět se nejedná o žádnou novinku, protože i tento koncept velmi dobře známe z datových sad Iris i California Housings.
4. Metadata a očekávané výsledky z datové sady Digits
V datové množině získané zavoláním funkce load_digits() nalezneme i další potenciálně užitečné informace. Jedná se především o názvy sloupců v případě, že budeme pole uložené v atributu data chápat jako tabulku (v tomto konkrétním případě o tabulku s 1797 řádky a 64 sloupci). Tyto sloupce se v oblasti zpracování dat taktéž nazývají atributy, což může být nepatrně matoucí.
Názvy sloupců takového pole jsou uloženy v atributu feature_names. A konečně v atributu target_names nalezneme jména tříd, které dohromady představují obor hodnot pro hodnoty target (tedy pro hodnoty, na které budeme model trénovat a s jejichž pomocí budeme ověřovat přesnost jeho předpovědí). Jak tyto informace vypadají konkrétně, nám prozradí další skript:
#!/usr/bin/env python
# import funkce, která vrátí obrázky pro práci
from sklearn.datasets import load_digits
# načtení obrázků, s nimiž budeme dále pracovat
digits_data = load_digits()
# zjištění základních informací o obrázcích
print("Description:", digits_data.DESCR)
print("Data:", digits_data.data.shape)
print("Obrázky:", digits_data.images.shape)
print("Feature names")
for feature_name in digits_data.feature_names:
print(feature_name)
print()
print("Target names")
for target_name in digits_data.target_names:
print(target_name)
# finito
Po spuštění tohoto skriptu se nejprve opět vypíšou informace o dvou n-rozměrných polích s trénovacími a verifikačními daty (což již známe):
Data: (1797, 64) Obrázky: (1797, 8, 8)
Dále se vypíšou názvy všech 64 sloupců pole data. Zde se prozrazuje to, co již vlastně víme z předchozí kapitoly – že v tomto poli jsou uloženy vektory s 64 hodnotami pixelů, které tvoří logický obrázek s rozlišením 8×8 pixelů:
Feature names pixel_0_0 pixel_0_1 pixel_0_2 pixel_0_3 pixel_0_4 pixel_0_5 pixel_0_6 pixel_0_7 pixel_1_0 pixel_1_1 pixel_1_2 pixel_1_3 ... ... ... pixel_6_5 pixel_6_6 pixel_6_7 pixel_7_0 pixel_7_1 pixel_7_2 pixel_7_3 pixel_7_4 pixel_7_5 pixel_7_6 pixel_7_7
Obsah pole target_names obsahuje u této datové množiny hodnoty „0“ až „9“, ovšem u jiných množin se může jednat o zcela odlišné informace (například „zapni kotel“/„vyplni kotel“, „před autem je chodec“ atd.):
Target names 0 1 2 3 4 5 6 7 8 9
Iris Data set: ---------------------------------------------------------------------------------------------------- Feature names: ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)'] ---------------------------------------------------------------------------------------------------- Target names: ['setosa' 'versicolor' 'virginica'] ----------------------------------------------------------------------------------------------------
California Housings: ---------------------------------------------------------------------------------------------------- Feature names: ['MedInc', 'HouseAge', 'AveRooms', 'AveBedrms', 'Population', 'AveOccup', 'Latitude', 'Longitude'] ---------------------------------------------------------------------------------------------------- Target names: ['MedHouseVal'] ----------------------------------------------------------------------------------------------------
5. Přečtení a následné vyobrazení jednotlivých ručně nakreslených číslic
V datové množině, kterou dokážeme přečíst funkcí load_digits, nalezneme (jak již víme) i atribut nazvaný images. Jedná se o n-rozměrné pole, konkrétně o trojrozměrné pole s velikostí 1797×8×8. Toto pole obsahuje 1797 matic velikosti 8×8 reprezentujících malé rastrové obrázky 8×8 pixelů, jejichž hodnoty jsou normalizovány do rozsahu 0..16 (to je důležité pro trénink modelu). Takové obrázky lze snadno zobrazit:
#!/usr/bin/env python
# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
# import funkce, která vrátí obrázky pro práci
from sklearn.datasets import load_digits
# načtení obrázků, s nimiž budeme dále pracovat
digits_data = load_digits()
# zjištění základních informací o obrázcích
print(digits_data.data.shape)
# vykreslení a uložení prvních deseti obrázků
for i in range(0, 10):
plt.matshow(digits_data.images[i])
# převod na stupně šedi
plt.gray()
plt.savefig(f"Grayscale image #{i}.png")
# vykreslení na obrazovku
plt.show()
# finito
Výsledkem by mělo být následujících deset grafů s vizualizací ručně psaných číslic 0 až 9 (nepoužíváme zde přitom žádnou interpolaci ani žádné další „vylepšení“ výsledků, které by mohl mozek špatně interpretovat):
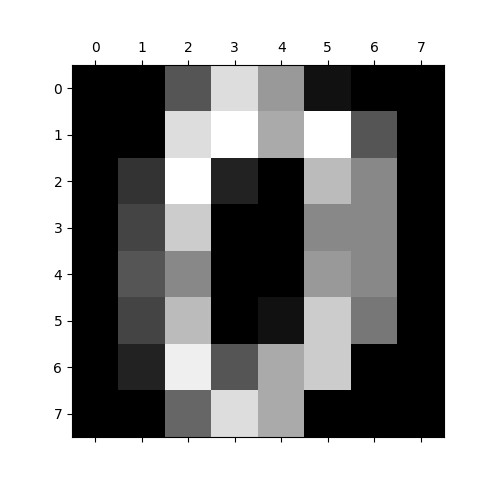
Obrázek 1: Vizualizace pole s číslicí 0 ve stupních šedi.
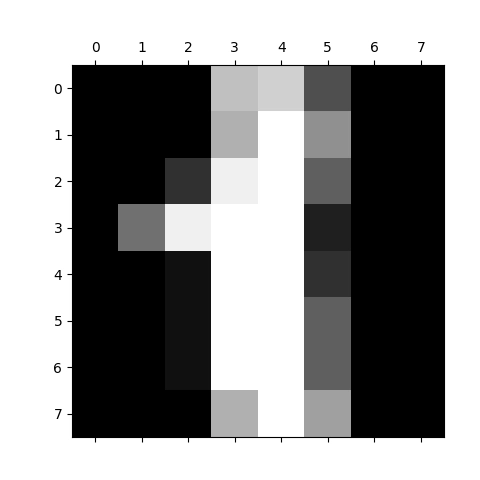
Obrázek 2: Vizualizace pole s číslicí 1 ve stupních šedi.
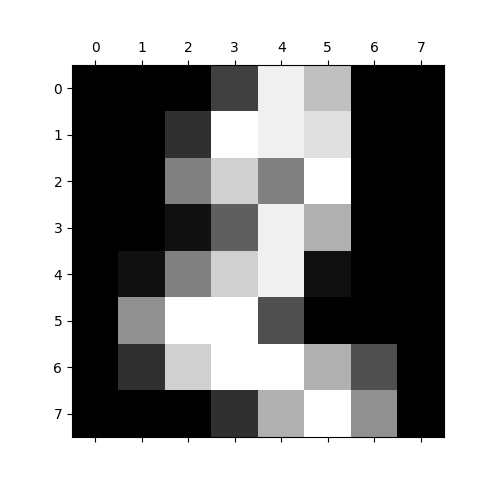
Obrázek 3: Vizualizace pole s číslicí 2 ve stupních šedi.
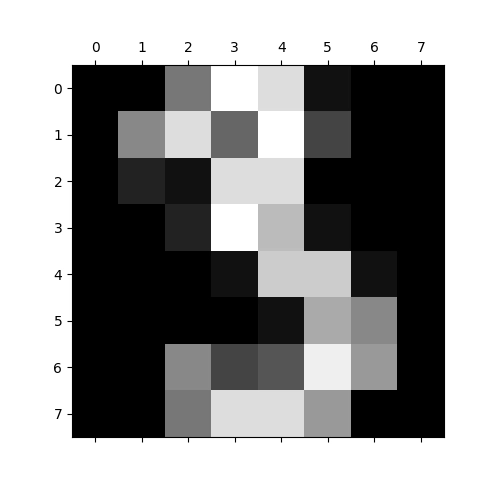
Obrázek 4: Vizualizace pole s číslicí 3 ve stupních šedi.
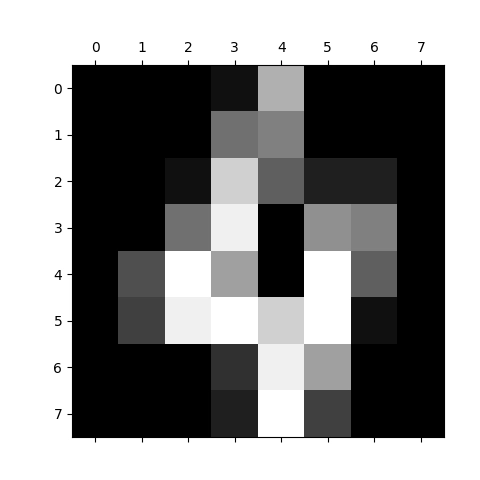
Obrázek 5: Vizualizace pole s číslicí 4 ve stupních šedi.
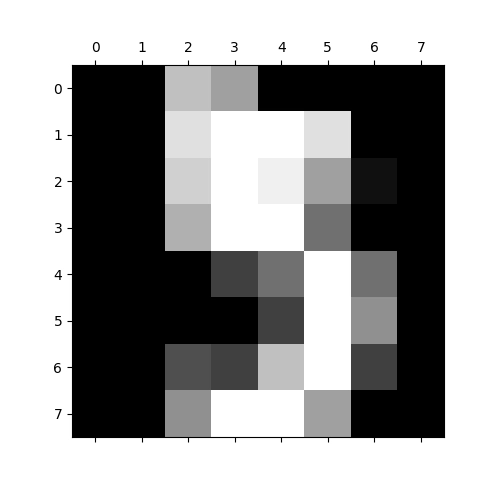
Obrázek 6: Vizualizace pole s číslicí 5 ve stupních šedi.
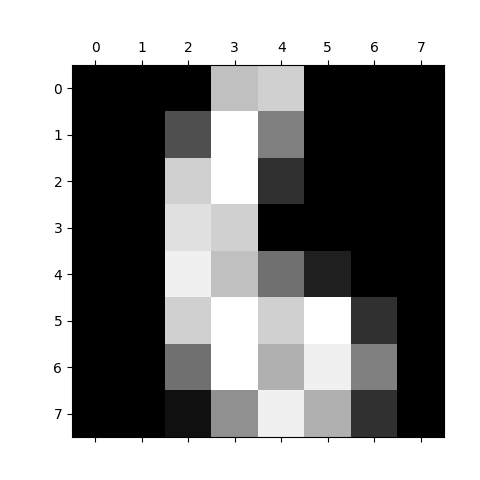
Obrázek 7: Vizualizace pole s číslicí 6 ve stupních šedi.
Obrázek 8: Vizualizace pole s číslicí 7 ve stupních šedi.
Obrázek 9: Vizualizace pole s číslicí 8 ve stupních šedi.
Obrázek 10: Vizualizace pole s číslicí 9 ve stupních šedi.
6. Rozpoznání číslic modelem provádějícím logistickou regresi
Pokusme se natrénovat model založený na logistické regresi (tedy jeden z nejjednodušších dostupných modelů) tak, aby rozpoznával jednotlivé číslice zapsané v rastru 8×8 pixelů. Model natrénujeme zcela standardním způsobem, tedy naprosto stejně, jako bychom to udělali s datovou sadou Iris. Jediným rozdílem je, že každý vstup nebude mít jen čtyři hodnoty (rozměry), ale 64 hodnot (pixely) a výsledek nemá obsahovat jen hodnotu 0, 1 nebo 2 (druh květiny) ale celočíselnou hodnotu z rozsahu 0 až 9:
# Rozpoznání obrazu s využitím knihovny scikit-learn
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import ConfusionMatrixDisplay
from sklearn.model_selection import cross_val_score
# Databáze ručně zapsaných číslic
from sklearn.datasets import load_digits
# načtení obrázků, s nimiž budeme dále pracovat
digits = load_digits()
# zjištění základních informací o obrázcích
print("Description:", digits.DESCR)
print("Data:", digits.data.shape)
print("Obrázky:", digits.images.shape)
# X je matice (feature matrix)
X = digits.data
# y je vektor (response vector)
y = digits.target
# rozdělení dat
trainX, testX, trainY, testY = train_test_split(X, y, test_size = 0.2)
print()
print("TrainX:", trainX.shape)
print("TrainY:", trainY.shape)
print("TestX:", testX.shape)
print("TestY:", testY.shape)
# provést klasifikaci
# konstrukce klasifikatoru
# (s hyperparametrem)
classifier = LogisticRegression(max_iter=1000)
# vypocet skore
scores = cross_val_score(classifier, X, y, cv=10, scoring="accuracy")
avg_score = scores.mean()
# vypsani prumerneho skore
print()
print("Accuracy:", avg_score)
print()
# trening noveho modelu
classifier = LogisticRegression(max_iter=1000)
classifier.fit(trainX, trainY)
class_names = digits.target_names
# absolutni hodnoty
disp = ConfusionMatrixDisplay.from_estimator(
classifier,
testX,
testY,
display_labels=class_names,
cmap=plt.cm.Blues,
normalize=None,
)
# zobrazeni matice
print(disp.confusion_matrix)
# ulozeni vysledku
plt.savefig("154_1.png")
# vizualizace matice
plt.show()
# relativni hodnoty
disp = ConfusionMatrixDisplay.from_estimator(
classifier,
testX,
testY,
display_labels=class_names,
cmap=plt.cm.Blues,
normalize="true",
)
# zobrazeni matice
print(disp.confusion_matrix)
# ulozeni vysledku
plt.savefig("154_2.png")
# vizualizace matice
plt.show()
7. Výsledky rozpoznání číslic modelem logistické regrese
Jaké budou výsledky tohoto modelu a jakou bude mít úspěšnost? Tyto údaje získáme ze skriptu z předchozí kapitoly velmi snadno. Nejdříve se zobrazí základní parametry datové sady a následně pak tvary trénovací i testovací datové sady po jejím rozdělení v poměru 1:5:
Data: (1797, 64) Obrázky: (1797, 8, 8) TrainX: (1437, 64) TrainY: (1437,) TestX: (360, 64) TestY: (360,)
Následně se zobrazí úspěšnost předpovědí natrénovaného modelu. Ta je relativně vysoká (cca 93%), i když jsme použili ten prakticky nejjednodušší dostupný model:
Accuracy: 0.9270856610800745
Přesnější informace nám ovšem dodají až matice záměn (confusion matrix) zobrazené jak s absolutními, tak i relativními hodnotami:
[[35 0 0 0 0 0 0 0 0 0] [ 0 34 0 1 1 0 0 0 0 0] [ 0 2 24 0 0 0 0 0 0 0] [ 0 0 0 33 0 1 0 0 0 0] [ 0 0 0 0 33 0 0 0 0 0] [ 0 0 0 0 0 41 0 0 0 1] [ 0 0 0 0 0 0 37 0 0 0] [ 0 0 0 0 0 0 0 40 0 0] [ 0 0 0 0 0 0 0 0 37 0] [ 0 0 0 0 0 2 0 0 1 37]] [[1. 0. 0. 0. 0. 0. 0. 0. 0. 0. ] [0. 0.94444444 0. 0.02777778 0.02777778 0. 0. 0. 0. 0. ] [0. 0.07692308 0.92307692 0. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 0.97058824 0. 0.02941176 0. 0. 0. 0. ] [0. 0. 0. 0. 1. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 0.97619048 0. 0. 0. 0.02380952] [0. 0. 0. 0. 0. 0. 1. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 1. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 1. 0. ] [0. 0. 0. 0. 0. 0.05 0. 0. 0.025 0.925 ]]
Vizuální podoba matic záměn:
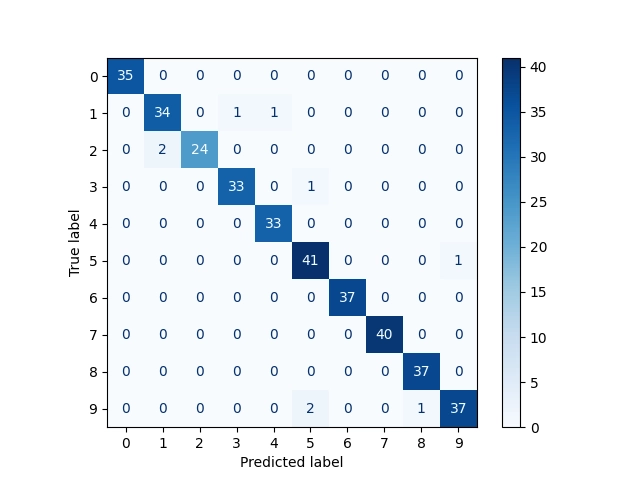
Obrázek 11: Matice záměn s absolutními odchylkami.
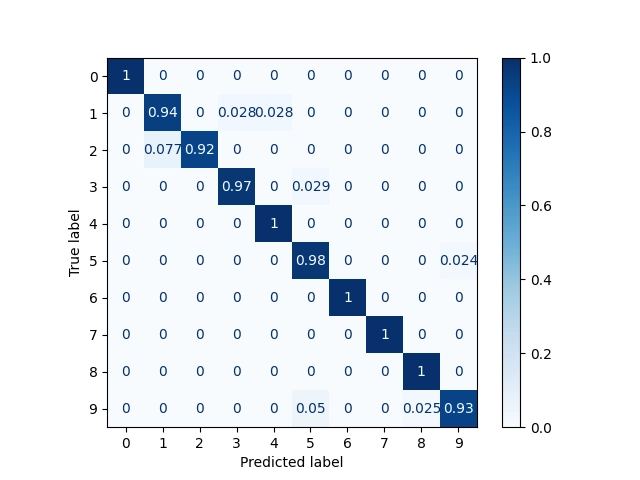
Obrázek 12: Matice záměn s relativními odchylkami.
8. Využití modelu SVM (metoda podpůrných vektorů) pro klasifikaci obrázků
Pro rozpoznání obrazů můžeme pochopitelně využít i sofistikovanější modely. Jedním z takových modelů je i model založený na metodě podpůrných vektorů neboli Support Vector Machine (SVM). Interně tato metoda provádí transformaci vstupů do odlišného prostoru, ve kterém se následně jednotlivé hodnoty rozdělují tak, aby to odpovídalo požadované klasifikaci (tři druhy kosatců, deset číslic atd.). Přepis původního skriptu tak, aby se využil model založený na SVM, je relativně snadnou úlohou, i když interní výpočty jsou v tomto případě již poměrně komplikované. Výsledek přitom vypadá následovně:
# Rozpoznání obrazu s využitím knihovny scikit-learn
import matplotlib.pyplot as plt
import numpy as np
from sklearn import svm
from sklearn.model_selection import train_test_split
from sklearn.metrics import ConfusionMatrixDisplay
from sklearn.model_selection import cross_val_score
# Databáze ručně zapsaných číslic
from sklearn.datasets import load_digits
# načtení obrázků, s nimiž budeme dále pracovat
digits = load_digits()
# zjištění základních informací o obrázcích
print("Description:", digits.DESCR)
print("Data:", digits.data.shape)
print("Obrázky:", digits.images.shape)
# X je matice (feature matrix)
X = digits.data
# y je vektor (response vector)
y = digits.target
# rozdělení dat
trainX, testX, trainY, testY = train_test_split(X, y, test_size = 0.2)
print()
print("TrainX:", trainX.shape)
print("TrainY:", trainY.shape)
print("TestX:", testX.shape)
print("TestY:", testY.shape)
# provést klasifikaci
# konstrukce klasifikatoru
# (s hyperparametrem)
classifier = svm.SVC(gamma=0.001)
# vypocet skore
scores = cross_val_score(classifier, X, y, cv=10, scoring="accuracy")
avg_score = scores.mean()
# vypsani prumerneho skore
print()
print("Accuracy:", avg_score)
print()
# trening modelu
classifier.fit(trainX, trainY)
class_names = digits.target_names
# absolutni hodnoty
disp = ConfusionMatrixDisplay.from_estimator(
classifier,
testX,
testY,
display_labels=class_names,
cmap=plt.cm.Blues,
normalize=None,
)
# zobrazeni matice
print(disp.confusion_matrix)
# ulozeni vysledku
plt.savefig("155_1.png")
# vizualizace matice
plt.show()
# relativni hodnoty
disp = ConfusionMatrixDisplay.from_estimator(
classifier,
testX,
testY,
display_labels=class_names,
cmap=plt.cm.Blues,
normalize="true",
)
# zobrazeni matice
print(disp.confusion_matrix)
# ulozeni vysledku
9. Výsledky rozpoznání číslic metodou podpůrných vektorů
Opět se podívejme na výsledky, které získáme po spuštění skriptu z předchozí kapitoly. Nyní bude úspěšnost předpovědí modelu mnohem větší – namísto necelých 93% jsme dosáhli téměř 98%:
Data: (1797, 64) Obrázky: (1797, 8, 8) TrainX: (1437, 64) TrainY: (1437,) TestX: (360, 64) TestY: (360,) Accuracy: 0.9782929857231533
Skript taktéž vypočítá a zobrazí matice záměn, které nyní vypadají následovně:
[[42 0 0 0 0 0 0 0 0 0] [ 0 29 0 0 0 0 0 0 0 0] [ 0 0 39 0 0 0 0 0 0 0] [ 0 0 0 33 0 0 0 1 0 0] [ 0 0 0 0 48 0 0 0 0 0] [ 0 0 0 0 0 41 0 0 0 1] [ 0 0 0 0 0 0 32 0 0 0] [ 0 0 0 0 0 0 0 35 0 0] [ 0 0 0 0 0 0 0 0 19 0] [ 0 0 0 0 0 0 0 1 1 38]] [[1. 0. 0. 0. 0. 0. 0. 0. 0. 0. ] [0. 1. 0. 0. 0. 0. 0. 0. 0. 0. ] [0. 0. 1. 0. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 0.97058824 0. 0. 0. 0.02941176 0. 0. ] [0. 0. 0. 0. 1. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 0.97619048 0. 0. 0. 0.02380952] [0. 0. 0. 0. 0. 0. 1. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 1. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 1. 0. ] [0. 0. 0. 0. 0. 0. 0. 0.025 0.025 0.95 ]]
Vizuální podoba matic záměn:
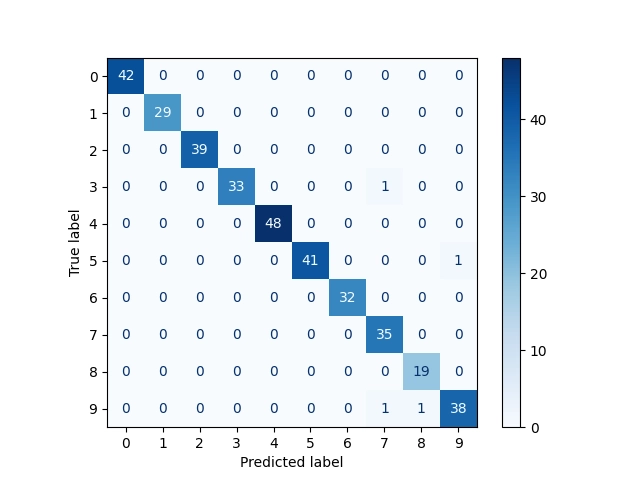
Obrázek 13: Matice záměn s absolutními odchylkami.
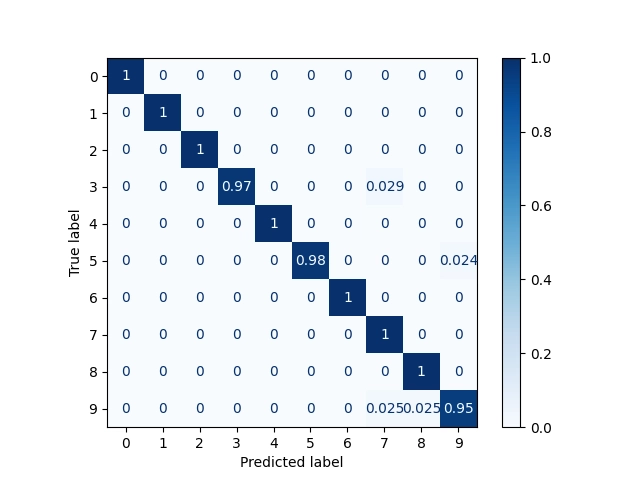
Obrázek 14: Matice záměn s relativními odchylkami.
10. Využití modelu pro hledání K nejbližších sousedů
Podobným způsobem můžeme nahradit předchozí model za model, který se snaží o hledání K nejbližších sousedů v natrénované sadě n-rozměrných bodů. Tento model je v knihovně scikit-learn implementován třídou KNeighborsClassifier. Pokusme se tedy tento model použít pro rozpoznání číslic v 64prvkových vektorech:
# Rozpoznání obrazu s využitím knihovny scikit-learn
import matplotlib.pyplot as plt
import numpy as np
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import ConfusionMatrixDisplay
from sklearn.model_selection import cross_val_score
# Databáze ručně zapsaných číslic
from sklearn.datasets import load_digits
# načtení obrázků, s nimiž budeme dále pracovat
digits = load_digits()
# zjištění základních informací o obrázcích
print("Description:", digits.DESCR)
print("Data:", digits.data.shape)
print("Obrázky:", digits.images.shape)
# X je matice (feature matrix)
X = digits.data
# y je vektor (response vector)
y = digits.target
# rozdělení dat
trainX, testX, trainY, testY = train_test_split(X, y, test_size = 0.2)
print()
print("TrainX:", trainX.shape)
print("TrainY:", trainY.shape)
print("TestX:", testX.shape)
print("TestY:", testY.shape)
# provést klasifikaci
# konstrukce klasifikatoru
# (s hyperparametrem)
classifier = KNeighborsClassifier(n_neighbors=5)
# vypocet skore
scores = cross_val_score(classifier, X, y, cv=10, scoring="accuracy")
avg_score = scores.mean()
# vypsani prumerneho skore
print()
print("Accuracy:", avg_score)
print()
# trening modelu
classifier.fit(trainX, trainY)
class_names = digits.target_names
# absolutni hodnoty
disp = ConfusionMatrixDisplay.from_estimator(
classifier,
testX,
testY,
display_labels=class_names,
cmap=plt.cm.Blues,
normalize=None,
)
# zobrazeni matice
print(disp.confusion_matrix)
# ulozeni vysledku
plt.savefig("156_1.png")
# vizualizace matice
plt.show()
# relativni hodnoty
disp = ConfusionMatrixDisplay.from_estimator(
classifier,
testX,
testY,
display_labels=class_names,
cmap=plt.cm.Blues,
normalize="true",
)
# zobrazeni matice
print(disp.confusion_matrix)
# ulozeni vysledku
11. Výsledky rozpoznání číslic modelem hledajícím K nejbližších sousedů
Přesnost předpovědí modelu KNeighborsClassifier je poměrně vysoká – přes 97%, což znamená, že jen tři procenta číslic se nerozeznají. Ostatně se podívejme, jak výsledky vypadají:
Data: (1797, 64) Obrázky: (1797, 8, 8) TrainX: (1437, 64) TrainY: (1437,) TestX: (360, 64) TestY: (360,) Accuracy: 0.9716294227188081
Matice záměn opět obsahuje největší hodnoty na hlavní diagonále, což je ostatně jen dobře (ideální by bylo získat čistě diagonální matici):
[[41 0 0 0 0 0 0 0 0 0] [ 0 36 0 0 0 0 0 0 0 0] [ 0 0 38 0 0 0 0 0 0 0] [ 0 0 0 35 0 0 0 0 0 0] [ 0 0 0 0 35 0 0 0 0 0] [ 0 0 0 0 0 30 1 0 0 1] [ 0 0 0 0 0 0 41 0 0 0] [ 0 0 0 0 0 0 0 31 0 0] [ 0 1 0 1 0 0 0 1 36 0] [ 0 0 0 0 1 0 0 0 0 31]]
[[1. 0. 0. 0. 0. 0. 0. 0. 0. 0. ] [0. 1. 0. 0. 0. 0. 0. 0. 0. 0. ] [0. 0. 1. 0. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 1. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 1. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 0.9375 0.03125 0. 0. 0.03125 ] [0. 0. 0. 0. 0. 0. 1. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 1. 0. 0. ] [0. 0.02564103 0. 0.02564103 0. 0. 0. 0.02564103 0.92307692 0. ] [0. 0. 0. 0. 0.03125 0. 0. 0. 0. 0.96875 ]]
Vizuální podoba matic záměn:
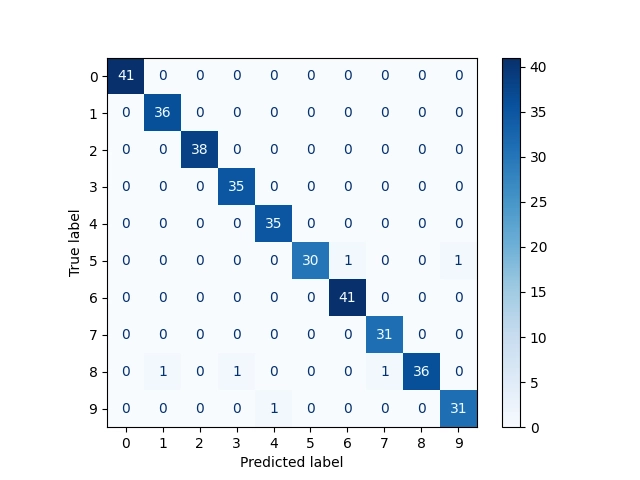
Obrázek 15: Matice záměn s absolutními odchylkami.
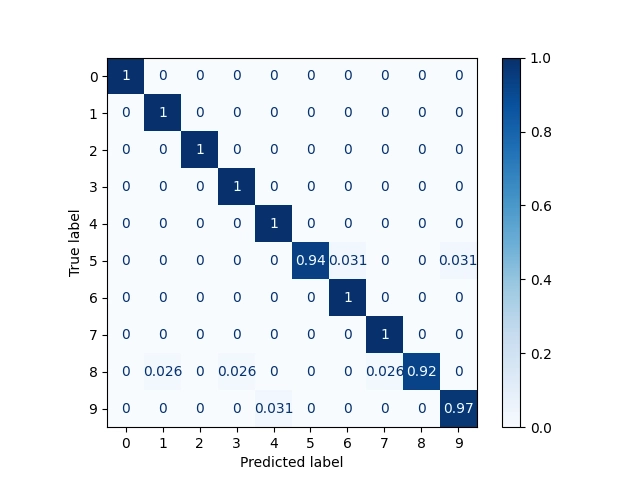
Obrázek 16: Matice záměn s relativními odchylkami.
12. Rozpoznání rastrových obrázků neuronovou sítí
Samozřejmě nám nic nebrání namísto „obyčejných modelů“ použít pro rozpoznání číslic neuronovou síť. Vzhledem k tomu, že provádíme klasifikaci (výstupem má být jedna celočíselná hodnota 0 až 9), použijeme pro realizaci neuronové sítě třídu MLPClassifier, s níž jsme se již seznámili předminule i minule. Upravme si tedy demonstrační příklad tak, aby se použil model založený na neuronové síti s výchozí konfigurací (100 neuronů v jediné skryté vrstvě):
# Rozpoznání obrazu s využitím knihovny scikit-learn
import matplotlib.pyplot as plt
import numpy as np
# model zalozeny na neuronove siti
from sklearn.neural_network import MLPClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import ConfusionMatrixDisplay
from sklearn.model_selection import cross_val_score
# Databáze ručně zapsaných číslic
from sklearn.datasets import load_digits
# načtení obrázků, s nimiž budeme dále pracovat
digits = load_digits()
# zjištění základních informací o obrázcích
print("Description:", digits.DESCR)
print("Data:", digits.data.shape)
print("Obrázky:", digits.images.shape)
# X je matice (feature matrix)
X = digits.data
# y je vektor (response vector)
y = digits.target
# rozdělení dat
trainX, testX, trainY, testY = train_test_split(X, y, test_size = 0.2)
print()
print("TrainX:", trainX.shape)
print("TrainY:", trainY.shape)
print("TestX:", testX.shape)
print("TestY:", testY.shape)
# provést klasifikaci
# konstrukce klasifikatoru
# (s hyperparametrem)
classifier = MLPClassifier(max_iter=5000)
# vypocet skore
scores = cross_val_score(classifier, X, y, cv=10, scoring="accuracy")
avg_score = scores.mean()
# vypsani prumerneho skore
print()
print("Accuracy:", avg_score)
print()
# trening modelu
classifier.fit(trainX, trainY)
class_names = digits.target_names
# absolutni hodnoty
disp = ConfusionMatrixDisplay.from_estimator(
classifier,
testX,
testY,
display_labels=class_names,
cmap=plt.cm.Blues,
normalize=None,
)
# zobrazeni matice
print(disp.confusion_matrix)
# ulozeni vysledku
plt.savefig("157_1.png")
# vizualizace matice
plt.show()
# relativni hodnoty
disp = ConfusionMatrixDisplay.from_estimator(
classifier,
testX,
testY,
display_labels=class_names,
cmap=plt.cm.Blues,
normalize="true",
)
# zobrazeni matice
print(disp.confusion_matrix)
# ulozeni vysledku
plt.savefig("157_2.png")
13. Výsledky rozpoznání číslic neuronovou sítí
Zajímavé je, že model založený na neuronové síti má přesnost rozpoznání pouze 95%, zatímco předchozí (interně jednodušší) model má přesnost vyšší o celá dvě procenta:
Accuracy: 0.9493482309124767
Opět se tedy ukazuje, že neuronové sítě pochopitelně mají své využití (a navíc si je ještě dokážeme doladit), ovšem v mnoha případech je jednodušší sáhnout po interně jednodušším modelu.
Struktura neuronové sítě: 3 vrstvy, ve vstupní vrstvě 64 neuronů, ve skryté vrstvě 100 neuronů a konečně ve výstupní vrstvě je deset neuronů:
Features: 64
Layers: 3
Outputs: 10
Weights:
0 (64, 100)
1 (100, 10)
Biases:
0 (100,)
1 (10,)
Vypočítat a zobrazit si můžeme i matici záměn – jak s absolutními hodnotami, tak i s hodnotami relativními:
[[31 0 0 0 0 0 1 0 0 0] [ 0 37 0 0 0 0 0 0 0 0] [ 0 0 35 0 0 0 0 0 0 0] [ 0 0 0 36 0 0 0 0 0 0] [ 0 0 0 0 32 0 0 0 1 0] [ 0 0 0 0 0 33 1 0 0 2] [ 0 0 0 0 0 0 35 0 0 0] [ 0 0 0 0 0 0 0 35 0 0] [ 0 2 0 0 0 0 0 0 33 0] [ 0 0 0 0 0 1 0 0 1 44]] [[0.96875 0. 0. 0. 0. 0. 0.03125 0. 0. 0. ] [0. 1. 0. 0. 0. 0. 0. 0. 0. 0. ] [0. 0. 1. 0. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 1. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 0.96969697 0. 0. 0. 0.03030303 0. ] [0. 0. 0. 0. 0. 0.91666667 0.02777778 0. 0. 0.05555556] [0. 0. 0. 0. 0. 0. 1. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 1. 0. 0. ] [0. 0.05714286 0. 0. 0. 0. 0. 0. 0.94285714 0. ] [0. 0. 0. 0. 0. 0.02173913 0. 0. 0.02173913 0.95652174]]
Vizuální podoba matic záměn:
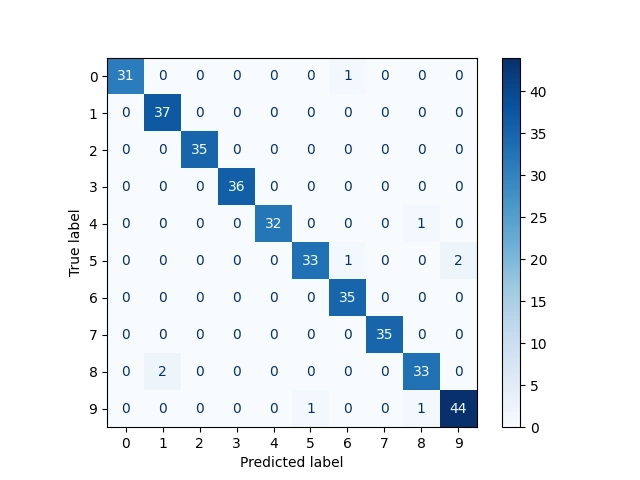
Obrázek 17: Matice záměn s absolutními odchylkami.
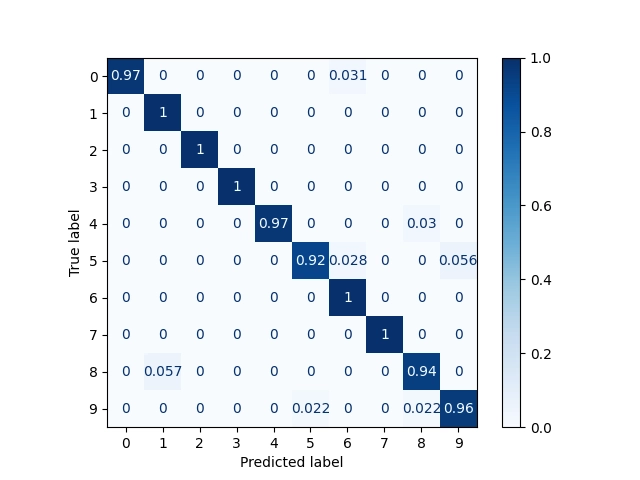
Obrázek 18: Matice záměn s relativními odchylkami.
14. Zobrazení původních obrázků i predikovaných výsledků ve vizuální podobě
Kromě matic záměn si můžeme vizualizovat i jednotlivé číslice v rastrové podobě (vstup) a odpovídající predikované výsledky. Jeden z možných způsobů, jak tento úkol řešit, je ukázán v dalším demonstračním příkladu, v němž je do jednoho grafu vykreslena mřížka s 25 obrázky, které jsou popsány výsledkem predikce – tj. jakou číslici na obrázku „vidí“ model. Některé odhady jsou přesné, jiné nikoli:
# Rozpoznání obrazu s využitím knihovny scikit-learn
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
# Databáze ručně zapsaných číslic
from sklearn.datasets import load_digits
# načtení obrázků, s nimiž budeme dále pracovat
digits = load_digits()
# zjištění základních informací o obrázcích
print("Description:", digits.DESCR)
print("Data:", digits.data.shape)
print("Obrázky:", digits.images.shape)
# X je matice (feature matrix)
X = digits.data
# y je vektor (response vector)
y = digits.target
for_training = len(y) * 8 // 10
print("Vzorků pro trénink:", for_training)
# rozdělení dat
trainX = X[:for_training]
testX = X[for_training:]
trainY = y[:for_training]
testY = y[for_training:]
# provést klasifikaci
# konstrukce klasifikatoru
# (s hyperparametrem)
classifier = LogisticRegression(max_iter=1000)
# vypocet skore
scores = cross_val_score(classifier, X, y, cv=10, scoring="accuracy")
avg_score = scores.mean()
print("Accuracy:", avg_score)
# trening modelu
classifier.fit(trainX, trainY)
predicted_labels = classifier.predict(testX)
images = digits.images[for_training:]
fig = plt.figure(figsize=(6.4, 8.0))
# zobrazit patnáct výsledků
for i in range(25):
predicted_digit = classifier.predict([testX[i]])[0]
correct_digit = testY[i]
print(predicted_digit, correct_digit)
image = images[i]
plt.subplot(5, 5, i+1)
plt.axis("off")
# zobrazení obrázku
plt.imshow(image, cmap=plt.cm.gray_r, interpolation="nearest")
# a přidání predikce - o jakou číslici se jedná
plt.title("Predict: %i" % predicted_digit)
# nakonec vše uložíme a zobrazíme
plt.savefig("158.png")
plt.show()
A takto bude vypadat graf s oněmi 25 číslicemi:

Obrázek 19: 25 ručně psaných číslic a příslušné odhady modelu.
15. Zobrazení těch číslic, u nichž se model spletl
Mnohem zajímavější však bude zjistit, které konkrétní číslice model naopak nerozeznal. To můžeme realizovat nepatrnou úpravou předchozího skriptu, a to tak, že vybereme jen ty rastrové obrázky, u nichž se model spletl. Takové obrázky si necháme zobrazit a současně si vypíšeme i predikovanou a korektní číslici, která se na obrázku nachází (protože mnohdy to nerozezná ani člověk):
wrong = 0
i = 0
while wrong < 25:
predicted_digit = classifier.predict([testX[i]])[0]
correct_digit = testY[i]
if predicted_digit != correct_digit:
print(predicted_digit, correct_digit)
image = images[i]
wrong += 1
plt.subplot(5, 5, wrong)
plt.axis("off")
# zobrazení obrázku
plt.imshow(image, cmap=plt.cm.gray_r, interpolation="nearest")
# a přidání predikce - o jakou číslici se jedná
plt.title(f"{predicted_digit} <> {correct_digit}")
i += 1
Celý skript po výše uvedené úpravě bude vypadat následovně:
# Rozpoznání obrazu s využitím knihovny scikit-learn
import matplotlib.pyplot as plt
import numpy as np
from sklearn import svm
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
# Databáze ručně zapsaných číslic
from sklearn.datasets import load_digits
# načtení obrázků, s nimiž budeme dále pracovat
digits = load_digits()
# zjištění základních informací o obrázcích
print("Description:", digits.DESCR)
print("Data:", digits.data.shape)
print("Obrázky:", digits.images.shape)
# X je matice (feature matrix)
X = digits.data
# y je vektor (response vector)
y = digits.target
for_training = len(y) * 6 // 10
print("Vzorků pro trénink:", for_training)
# rozdělení dat
trainX = X[:for_training]
testX = X[for_training:]
trainY = y[:for_training]
testY = y[for_training:]
# provést klasifikaci
# konstrukce klasifikatoru
# (s hyperparametrem)
#classifier = LogisticRegression(max_iter=1000)
classifier = svm.SVC(gamma=0.001)
# vypocet skore
scores = cross_val_score(classifier, X, y, cv=10, scoring="accuracy")
avg_score = scores.mean()
print("Accuracy:", avg_score)
# trening modelu
classifier.fit(trainX, trainY)
predicted_labels = classifier.predict(testX)
images = digits.images[for_training:]
fig = plt.figure(figsize=(6.4, 8.0))
# zobrazit patnáct výsledků
wrong = 0
i = 0
while wrong < 25:
predicted_digit = classifier.predict([testX[i]])[0]
correct_digit = testY[i]
if predicted_digit != correct_digit:
print(predicted_digit, correct_digit)
image = images[i]
wrong += 1
plt.subplot(5, 5, wrong)
plt.axis("off")
# zobrazení obrázku
plt.imshow(image, cmap=plt.cm.gray_r, interpolation="nearest")
# a přidání predikce - o jakou číslici se jedná
plt.title(f"{predicted_digit} <> {correct_digit}")
i += 1
# nakonec vše uložíme a zobrazíme
plt.savefig("159.png")
plt.show()
16. Graf s číslicemi, které nebyly správně rozeznány
Z výsledného grafu, v němž jsou zobrazeny číslice, které model rozeznal nesprávně, můžeme vidět určité vzory, tj. „typy“ zkreslení, s nimiž si model neví rady a které špatně odhadne (a navíc prakticky vždy špatně vrátí stejnou číslici):

Obrázek 20: Graf s číslicemi, které nebyly modelem správně rozeznány.
17. Zobrazení číslic, které nebyly korektně rozeznány neuronovou sítí
Naprosto stejným způsobem si můžeme nechat zobrazit číslice, které nebyly korektně rozpoznány neuronovou sítí, tj. tím nejsložitějším modelem, který až doposud máme k dispozici. Skript tedy upravíme jen nepatrně, konkrétně tak, aby se použil model realizovaný třídou MLPClassifier, který ovšem nemá tak dobrou predikční schopnost, jako například SVM nebo KNeighborsClassifier, tedy alespoň v případě, že výslednou neuronovou síť nebudeme dále „ladit“:
# Rozpoznání obrazu s využitím knihovny scikit-learn
import matplotlib.pyplot as plt
import numpy as np
from sklearn.neural_network import MLPClassifier
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
# Databáze ručně zapsaných číslic
from sklearn.datasets import load_digits
# načtení obrázků, s nimiž budeme dále pracovat
digits = load_digits()
# zjištění základních informací o obrázcích
print("Description:", digits.DESCR)
print("Data:", digits.data.shape)
print("Obrázky:", digits.images.shape)
# X je matice (feature matrix)
X = digits.data
# y je vektor (response vector)
y = digits.target
for_training = len(y) * 6 // 10
print("Vzorků pro trénink:", for_training)
# rozdělení dat
trainX = X[:for_training]
testX = X[for_training:]
trainY = y[:for_training]
testY = y[for_training:]
# provést klasifikaci
# konstrukce klasifikatoru
# (s hyperparametrem)
#classifier = LogisticRegression(max_iter=1000)
classifier = MLPClassifier(max_iter=5000)
# vypocet skore
scores = cross_val_score(classifier, X, y, cv=10, scoring="accuracy")
avg_score = scores.mean()
print("Accuracy:", avg_score)
# trening modelu
classifier.fit(trainX, trainY)
predicted_labels = classifier.predict(testX)
images = digits.images[for_training:]
fig = plt.figure(figsize=(6.4, 8.0))
# zobrazit 25 výsledků
wrong = 0
i = 0
while wrong < 25:
predicted_digit = classifier.predict([testX[i]])[0]
correct_digit = testY[i]
if predicted_digit != correct_digit:
print(predicted_digit, correct_digit)
image = images[i]
wrong += 1
plt.subplot(5, 5, wrong)
plt.axis("off")
# zobrazení obrázku
plt.imshow(image, cmap=plt.cm.gray_r, interpolation="nearest")
# a přidání predikce - o jakou číslici se jedná
plt.title(f"{predicted_digit} <> {correct_digit}")
i += 1
# nakonec vše uložíme a zobrazíme
plt.savefig("160.png")
plt.show()
18. Číslice, které nebyly rozpoznány neuronovou sítí
Při porovnání obrázků číslo 20 a 21 je zřejmé, že neuronová síť nedokáže rozeznat odlišné vzory v porovnání s jednoduššími modely. To je zajímavé zjištění. Příště si ukážeme, jak kvalitu neuronové sítě ovlivňuje volba aktivační funkce, což je většinou globální nastavení pro celou neuronovou síť (i když někdy může být vhodnější zvolit si vlastní aktivační funkci pro každou vrstvu zvlášť).

Obrázek 21: Graf s číslicemi, které nebyly neuronovou sítí správně rozeznány.
19. Repositář s demonstračními příklady
Všechny demonstrační příklady využívající knihovnu Scikit-learn lze nalézt v repositáři https://github.com/tisnik/most-popular-python-libs. Následují odkazy na jednotlivé příklady i na (Jupyter) diáře s postupem výpočtů a analýz:
V repositáři nalezneme taktéž projektový soubor a Jupyter Notebook s vysvětlením, jak lze modely využít pro rozpoznávání obsahu rastrových obrázků:
| # | Příklad | Stručný popis | Adresa příkladu |
|---|---|---|---|
| 1 | pyproject.toml | projektový soubor (pro PDM) se všemi závislostmi | https://github.com/tisnik/most-popular-python-libs/blob/master/sklearn/pyproject.toml |
| 2 | pdm.lock | lock soubor s konkrétními verzemi všech přímých i tranzitivních závislostí | https://github.com/tisnik/most-popular-python-libs/blob/master/sklearn/pdm.lock |
| 3 | Rozpoznání_obrazu_scikit-learn.ipynb | Jupyter notebook s celým postupem | https://github.com/tisnik/most-popular-python-libs/blob/master/sklearn/Rozpoznání_obrazu_scikit-learn.ipynb |
| 4 | particle_life.py | emergence: příklad vzniku struktury | https://github.com/tisnik/most-popular-python-libs/blob/master/particles/particle_life.py |
20. Odkazy na Internetu
- Shluková analýza (clustering) a knihovna Scikit-learn
https://www.root.cz/clanky/shlukova-analyza-clustering-a-knihovna-scikit-learn/ - Shluková analýza (clustering) a knihovna Scikit-learn (2)
https://www.root.cz/clanky/shlukova-analyza-clustering-a-knihovna-scikit-learn-2/ - Shluková analýza (clustering) a knihovna Scikit-learn (z plochy do 3D prostoru)
https://www.root.cz/clanky/shlukova-analyza-clustering-a-knihovna-scikit-learn-z-plochy-do-3d-prostoru/ - Rozpoznávání obrázků knihovnou Scikit-learn: první kroky
https://www.root.cz/clanky/rozpoznavani-obrazku-knihovnou-scikit-learn-prvni-kroky/ - scikit-learn: Machine Learning in Python
https://scikit-learn.org/stable/index.html - Sklearn-pandas
https://github.com/scikit-learn-contrib/sklearn-pandas - sklearn-xarray
https://github.com/phausamann/sklearn-xarray/ - Clustering
https://scikit-learn.org/stable/modules/clustering.html - Cluster analysis (Wikipedia)
https://en.wikipedia.org/wiki/Cluster_analysis - Shluková analýza (Wikipedia)
https://cs.wikipedia.org/wiki/Shlukov%C3%A1_anal%C3%BDza - K-means
https://cs.wikipedia.org/wiki/K-means - k-means clustering
https://en.wikipedia.org/wiki/K-means_clustering - Spectral clustering
https://en.wikipedia.org/wiki/Spectral_clustering - Emergence
https://cs.wikipedia.org/wiki/Emergence - Particle Life: Vivid structures from rudimentary rules
https://particle-life.com/ - Hertzsprungův–Russellův diagram
https://cs.wikipedia.org/wiki/Hertzsprung%C5%AFv%E2%80%93Russell%C5%AFv_diagram - Using Machine Learning in an HR Diagram
https://cocalc.com/share/public_paths/08b6e03583cbdef3cdb9813a54ec68ff773c747f - Gaia H-R diagrams: Querying Gaia data for one million nearby stars
https://vlas.dev/post/gaia-dr2-hrd/ - The Hertzsprung–Russell diagram
https://scipython.com/book2/chapter-9-data-analysis-with-pandas/problems/p92/the-hertzsprung-russell-diagram/ - Animated Hertzsprung-Russell Diagram with 119,614 datapoints
https://github.com/zonination/h-r-diagram - Neuraxle Pipelines
https://github.com/Neuraxio/Neuraxle - scikit-learn: Getting Started
https://scikit-learn.org/stable/getting_started.html - Support Vector Machines
https://scikit-learn.org/stable/modules/svm.html - Use Deep Learning to Detect Programming Languages
http://searene.me/2017/11/26/use-neural-networks-to-detect-programming-languages/ - Natural-language processing
https://en.wikipedia.org/wiki/Natural-language_processing - THE MNIST DATABASE of handwritten digits
http://yann.lecun.com/exdb/mnist/ - MNIST database (Wikipedia)
https://en.wikipedia.org/wiki/MNIST_database - MNIST For ML Beginners
https://www.tensorflow.org/get_started/mnist/beginners - Stránka projektu Torch
http://torch.ch/ - Torch: Serialization
https://github.com/torch/torch7/blob/master/doc/serialization.md - Torch: modul image
https://github.com/torch/image/blob/master/README.md - Data pro neuronové sítě
http://archive.ics.uci.edu/ml/index.php - Torch na GitHubu (několik repositářů)
https://github.com/torch - Torch (machine learning), Wikipedia
https://en.wikipedia.org/wiki/Torch_%28machine_learning%29 - Torch Package Reference Manual
https://github.com/torch/torch7/blob/master/README.md - Torch Cheatsheet
https://github.com/torch/torch7/wiki/Cheatsheet - Neural network containres (Torch)
https://github.com/torch/nn/blob/master/doc/containers.md - Simple layers
https://github.com/torch/nn/blob/master/doc/simple.md#nn.Linear - Transfer Function Layers
https://github.com/torch/nn/blob/master/doc/transfer.md#nn.transfer.dok - Feedforward neural network
https://en.wikipedia.org/wiki/Feedforward_neural_network - Biologické algoritmy (4) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-4-neuronove-site/ - Biologické algoritmy (5) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-5-neuronove-site/ - Umělá neuronová síť (Wikipedia)
https://cs.wikipedia.org/wiki/Um%C4%9Bl%C3%A1_neuronov%C3%A1_s%C3%AD%C5%A5 - PyTorch
http://pytorch.org/ - JupyterLite na PyPi
https://pypi.org/project/jupyterlite/ - JupyterLite na GitHubu
https://github.com/jupyterlite/jupyterlite - Dokumentace k projektu JupyterLite
https://github.com/jupyterlite/jupyterlite - Matplotlib Home Page
http://matplotlib.org/ - Matplotlib (Wikipedia)
https://en.wikipedia.org/wiki/Matplotlib - Popis barvových map modulu matplotlib.cm
https://gist.github.com/endolith/2719900#id7 - Ukázky (palety) barvových map modulu matplotlib.cm
http://matplotlib.org/examples/color/colormaps_reference.html - Galerie grafů vytvořených v Matplotlibu
https://matplotlib.org/3.2.1/gallery/ - 3D rendering
https://en.wikipedia.org/wiki/3D_rendering - 3D computer graphics
https://en.wikipedia.org/wiki/3D_computer_graphics - Primary 3D view planes
https://matplotlib.org/stable/gallery/mplot3d/view_planes_3d.html - Getting started in scikit-learn with the famous iris dataset
https://www.youtube.com/watch?v=hd1W4CyPX58 - Training a machine learning model with scikit-learn
https://www.youtube.com/watch?v=RlQuVL6-qe8 - Iris (plant)
https://en.wikipedia.org/wiki/Iris_(plant) - Kosatec
https://cs.wikipedia.org/wiki/Kosatec - Iris setosa
https://en.wikipedia.org/wiki/Iris_setosa - Iris versicolor
https://en.wikipedia.org/wiki/Iris_versicolor - Iris virginica
https://en.wikipedia.org/wiki/Iris_virginica - Druh
https://cs.wikipedia.org/wiki/Druh - Iris subg. Limniris
https://en.wikipedia.org/wiki/Iris_subg._Limniris - Iris Dataset Classification with Python: A Tutorial
https://www.pycodemates.com/2022/05/iris-dataset-classification-with-python.html - Iris flower data set
https://en.wikipedia.org/wiki/Iris_flower_data_set - List of datasets for machine-learning research
https://en.wikipedia.org/wiki/List_of_datasets_for_machine-learning_research - Analýza hlavních komponent
https://cs.wikipedia.org/wiki/Anal%C3%BDza_hlavn%C3%ADch_komponent - Principal component analysis
https://en.wikipedia.org/wiki/Principal_component_analysis - Scikit-learn Crash Course – Machine Learning Library for Python
https://www.youtube.com/watch?v=0B5eIE_1vpU - calm-notebooks
https://github.com/koaning/calm-notebooks - Should you teach Python or R for data science?
https://www.dataschool.io/python-or-r-for-data-science/ - nbviewer: A simple way to share Jupyter Notebooks
https://nbviewer.org/ - AI vs Machine Learning (Youtube)
https://www.youtube.com/watch?v=4RixMPF4×is - Machine Learning | What Is Machine Learning? | Introduction To Machine Learning | 2024 | Simplilearn (Youtube)
https://www.youtube.com/watch?v=ukzFI9rgwfU - A Gentle Introduction to Machine Learning (Youtube)
https://www.youtube.com/watch?v=Gv9_4yMHFhI - Machine Learning vs Deep Learning
https://www.youtube.com/watch?v=q6kJ71tEYqM - Umělá inteligence (slajdy)
https://slideplayer.cz/slide/12119218/ - Úvod do umělé inteligence
https://slideplayer.cz/slide/2505525/ - Umělá inteligence I / Artificial Intelligence I
https://ktiml.mff.cuni.cz/~bartak/ui/ - Matplotlib vs. seaborn vs. Plotly vs. MATLAB vs. ggplot2 vs. pandas
https://ritza.co/articles/matplotlib-vs-seaborn-vs-plotly-vs-MATLAB-vs-ggplot2-vs-pandas/ - Matplotlib, Seaborn or Plotnine?
https://www.reddit.com/r/datascience/comments/jvrqxt/matplotlib_seaborn_or_plotnine/ - @Rabeez: Rabeez/plotting_comparison.ipynb
https://gist.github.com/Rabeez/ffc0b59d4a41e20fa8d944c44a96adbc - Matplotlib, Seaborn, Plotly and Plotnine Comparison
https://python.plainenglish.io/matplotlib-seaborn-plotly-and-plotnine-comparison-baf2db5a9c40 - Data Visualization 101: How to Choose a Python Plotting Library
https://towardsdatascience.com/data-visualization-101-how-to-choose-a-python-plotting-library-853460a08a8a - Data science in Python: pandas, seaborn, scikit-learn
https://www.youtube.com/watch?v=3ZWuPVWq7p4 - 7.2. Real world datasets
https://scikit-learn.org/stable/datasets/real_world.html#california-housing-dataset - 7.2.7. California Housing dataset
https://scikit-learn.org/stable/datasets/real_world.html#california-housing-dataset - Comprehensive Guide to Classification Models in Scikit-Learn
https://www.geeksforgeeks.org/comprehensive-guide-to-classification-models-in-scikit-learn/ - Tidy Data Visualization: ggplot2 vs seaborn
https://blog.tidy-intelligence.com/posts/ggplot2-vs-seaborn/ - seaborn: statistical data visualization
https://seaborn.pydata.org/ - Linear regression (Wikipedia)
https://en.wikipedia.org/wiki/Linear_regression - Lineární regrese (Wikipedia)
https://cs.wikipedia.org/wiki/Line%C3%A1rn%C3%AD_regrese - Iris Flower Classification with MLP Classifier
https://www.metriccoders.com/post/iris-flower-classification-with-mlp-classifier