Obsah
1. Jednoduchý a současně i univerzální model lineární regrese
2. Krátké zopakování – lineární regrese bodů ležících v rovině
3. Vliv hyperparametru fit_intercept na výpočet směrnice a posunu přímky
4. Lineární regrese při vynucení w0=0 pro obecná data
5. Lineární regrese při vynucení w0=0 v případě, že vstupní body obsahují počátek souřadného systému
6. Model lineární regrese pro větší množství předpovídaných hodnot
7. Model předpovídající pro každou vstupní hodnotu dvě výstupní hodnoty (odpovědi)
8. Lineární regrese a proložení bodů rovinou
9. Konstrukce matice obsahující souřadnice bodů v mřížce
10. Proložení bodů v prostoru rovinou
11. Proložení rovinou při přidání náhodnosti do pozic bodů v prostoru
12. Kombinace předchozích příkladů: přechod z roviny do prostoru a více sad očekávaných výsledků
13. Proložení dvou sad bodů dvěma nezávislými rovinami
14. Přidání náhodné výšky bodů v datové sadě
16. Příklad jednoduché polynomické regrese
17. Proložení bodů v prostoru plochou prvního stupně (rovinou)
18. Proložení bodů v prostoru plochou druhého stupně
19. Repositář s demonstračními příklady
1. Jednoduchý a současně i univerzální model lineární regrese
V dnešním článku o knihovně scikit-learn se ještě jednou vrátíme k modelu pro lineární regresi. S tímto modelem jsme se již setkali, ovšem ve skutečnosti je i zdánlivě jednoduchý až triviální koncept lineární regrese realizován takovým způsobem, že ho lze využít mnoha různými způsoby, například:
- Proložení bodů v rovině přímkou (nejjednodušší použití)
- Proložení bodů v prostoru rovinou
- Dtto pro vyšší dimenze (body v X-rozměrném prostoru proloženy X-1 rozměrným lineárním objektem)
- Model lze použít pro větší množství neznámých (odhadovaných hodnot), takže se interně uloží informace o dvou přímkách/rovinách atd.
- Přímka/rovina je určena parametry ležícími v oblasti (prostoru) nikoli vstupních hodnot, ale prostoru parametrů, což nám umožňuje realizovat například polynomickou regresi i další formy regrese (sinus atd.).
- Předchozí koncepty lze navíc zkombinovat, což si ukážeme na proložení bodů v prostoru plochou druhého stupně (popsanou polynomem druhého řádu).
2. Krátké zopakování – lineární regrese bodů ležících v rovině
S modelem (resp. přesněji řečeno s modely) založenými na lineární regresi jsme se již, jak bylo napsáno v úvodní kapitole, setkali. Připomeňme si ten nejjednodušší možný případ, a tím je proložení bodů ležících v rovině vhodně zvolenou přímkou. Směrnice a posun přímky je vypočítán takovým způsobem, aby součet čtverců odchylky (vzdálenosti) od bodů byl co nejmenší.
Nejprve zkonstruujeme dva vektory, přičemž první vektor bude obsahovat x-ové souřadnice bodů a druhý vektor souřadnice y-ové. Z kódu je zřejmé, že se body budou odchylovat od ideální přímky o náhodnou hodnotu:
# x je vektor x = np.linspace(0, 10, VALUES) # y je vektor y = np.linspace(-1, 1, VALUES) + 0.5*np.random.rand(VALUES)
Model lineární regrese počítá s tím, že známé vstupní údaje jsou uloženy v matici a nikoli ve vektoru, takže provedeme příslušný převod (X značí matici, je to velké písmeno):
# převod vektoru na 2D matici X = x.reshape(-1, 1)
Provedeme trénink modelu se všemi body (což v praxi nebude možné a ani ideální řešení):
# konstrukce modelu lr = linear_model.LinearRegression() # trénink modelu (X musí být maticí) lr.fit(X, y)
Následně spočítáme predikci modelu, tj. vlastně přímku s minimálními možnými odchylkami od vstupních bodů:
# predikce modelu
y_pred = lr.predict(X)
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", lr.coef_)
print("Intercept: \n", lr.intercept_)
Skript, jehož zdrojový kód je zde zobrazen, navíc body i predikci modelu (přímku) vykreslí:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# počet vzorků ve vektorech x i y
VALUES = 50
# x je vektor
x = np.linspace(0, 10, VALUES)
# y je vektor
y = np.linspace(-1, 1, VALUES) + 0.5*np.random.rand(VALUES)
# převod vektoru na 2D matici
X = x.reshape(-1, 1)
# tvar matice X a vektoru y
print("X shape:", X.shape)
print("y shape:", y.shape)
# konstrukce modelu
lr = linear_model.LinearRegression()
# trénink modelu (X musí být maticí)
lr.fit(X, y)
# predikce modelu
y_pred = lr.predict(X)
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", lr.coef_)
print("Intercept: \n", lr.intercept_)
# vykreslení výsledku
plt.scatter(x, y, color="black", s=2)
plt.plot(x, y_pred, color="blue", linewidth=2)
# titulek grafu
plt.title("Linear regression")
# osy
plt.xticks()
plt.yticks()
# ulozeni diagramu do souboru
plt.savefig("112.png")
# zobrazeni diagramu
plt.show()
Výsledkem by měl být následující graf ukazující, jakým způsobem došlo k proložení bodů v rovině přímkou:
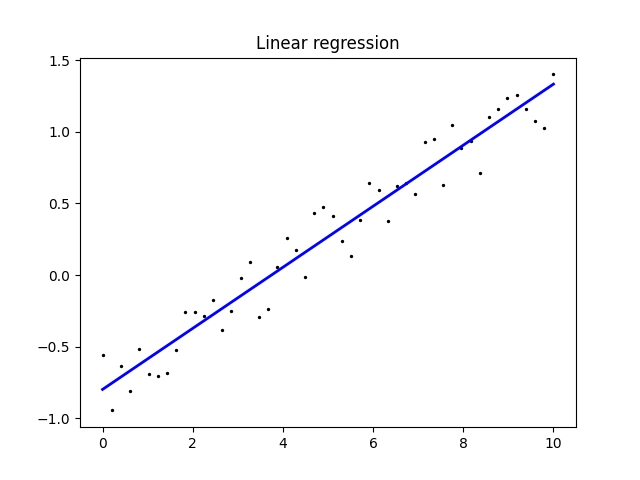
Obrázek 1: Proložení bodů v rovině přímkou.
Současně se vypíšou parametry přímky, což jsou vlastně informace, které se model naučil:
X shape: (50, 1) y shape: (50,) Coefficients: [0.19903235] Intercept: -0.7268848393877398
V tomto případě má přímka směrnici 0,199 a posun –0,72688…, její rovnice je tedy:
y = 0,199x - 0,72688
Ve skutečnosti není nutné, aby x-ové souřadnice bodů byly od sebe vzdáleny o konstantní hodnotu. Namísto:
# x je vektor x = np.linspace(0, 10, VALUES)
můžeme přidat nějakou (pseuodo)náhodnou hodnotu ke všem souřadnicím:
# x je vektor x = np.linspace(0, 10, VALUES) + 0.5*np.random.rand(VALUES)
Výsledek může vypadat následovně:
X shape: (50, 1) y shape: (50,) Coefficients: [0.19975871] Intercept: -0.8328002402028932
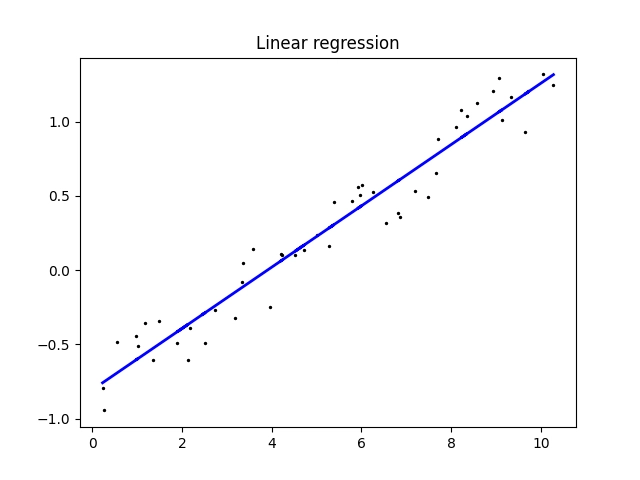
Obrázek 2: Proložení bodů v rovině přímkou, přičemž x-ové i y-ové souřadnice bodů obecně neleží na pravidelné mřížce.
3. Vliv hyperparametru fit_intercept na výpočet směrnice a posunu přímky
Při konstrukci modelu pro lineární regresi je možné zvolit hyperparametr fit_intercept, přesněji řečeno povolit či zakázat výpočet posunu přímky (nebo podobného objektu ve více dimenzích). Interně totiž model při predikci vyhodnocuje tento výraz:
y(w, x) = w0 + w1 x1 + w2 x2 + … + wp xp
Přičemž člen w0 může být buď nulový nebo vypočten při tréninku modelu. A právě vynucení toho, aby byl w0 nulový, řídíme hyperparametrem fit_intercept:
# konstrukce modelu lr = linear_model.LinearRegression(fit_intercept=False)
4. Lineární regrese při vynucení w0=0 pro obecná data
Pokusme se nyní o natrénování modelu pro lineární regresi, přičemž si vynutíme, aby byl posun výsledné přímky nulový, tj. aby platilo w0=0. Použijeme tedy hyperparametr fit_intercept nastavený explicitně na hodnotu False:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# počet vzorků ve vektorech x i y
VALUES = 50
# x je vektor
x = np.linspace(0, 10, VALUES)
# y je vektor
y = np.linspace(-1, 1, VALUES) + 0.5*np.random.rand(VALUES)
# převod vektoru na 2D matici
X = x.reshape(-1, 1)
# tvar matice X a vektoru y
print("X shape:", X.shape)
print("y shape:", y.shape)
# konstrukce modelu
lr = linear_model.LinearRegression(fit_intercept=False)
# trénink modelu (X musí být maticí)
lr.fit(X, y)
# predikce modelu
y_pred = lr.predict(X)
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", lr.coef_)
print("Intercept: \n", lr.intercept_)
# vykreslení výsledku
plt.scatter(x, y, color="black", s=2)
plt.plot(x, y_pred, color="blue", linewidth=2)
# titulek grafu
plt.title("Linear regression")
# osy
plt.xticks()
plt.yticks()
# ulozeni diagramu do souboru
plt.savefig("113.png")
# zobrazeni diagramu
plt.show()
Z výstupu zobrazeného skriptem je patrné, že se změnila směrnice přímky a současně je její posun nulový (což jsme požadovali):
X shape: (50, 1) y shape: (50,) Coefficients: [0.08292883] Intercept: 0.0
V tomto případě je tedy přímka určená rovnici:
y = 0,08292883x
Z vykresleného grafu je navíc patrné, že model nedokázal proložit body vhodnou přímkou, protože byl omezen jejím nulovým posunem:
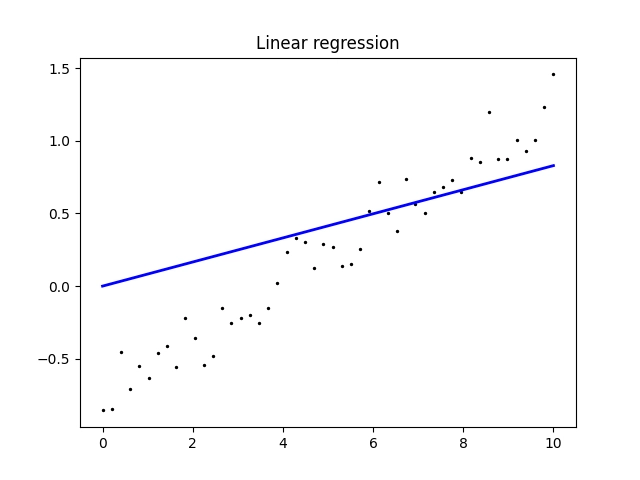
Obrázek 3: Proložení bodů v rovině přímkou, která prochází počátkem souřadného systému.
5. Lineární regrese při vynucení w0=0 v případě, že vstupní body obsahují počátek souřadného systému
V případě, že vstupní body tvoří shluk, který prochází (v blízkosti) počátku souřadného systému, můžeme se pokusit o vynucení w0=0, tedy toho, aby výsledná přímka procházela přesně středem souřadného systému.
Příklad úpravy obsahu vektorů x a y:
# x je vektor x = np.linspace(0, 10, VALUES) # y je vektor y = np.linspace(0, 2, VALUES) + 0.5*np.random.rand(VALUES)
nebo ještě lépe; zajistíme, aby byly body ve vektoru y umístěny okolo ideální hodnoty symetricky:
# x je vektor x = np.linspace(0, 10, VALUES) # y je vektor y = np.linspace(0, 2, VALUES) + 0.5*np.random.rand(VALUES) - 0.25
Upravený skript vypadá následovně:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# počet vzorků ve vektorech x i y
VALUES = 50
# x je vektor
x = np.linspace(0, 10, VALUES)
# y je vektor
y = np.linspace(0, 2, VALUES) + 0.5*np.random.rand(VALUES)
# převod vektoru na 2D matici
X = x.reshape(-1, 1)
# tvar matice X a vektoru y
print("X shape:", X.shape)
print("y shape:", y.shape)
# konstrukce modelu
lr = linear_model.LinearRegression(fit_intercept=False)
# trénink modelu (X musí být maticí)
lr.fit(X, y)
# predikce modelu
y_pred = lr.predict(X)
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", lr.coef_)
print("Intercept: \n", lr.intercept_)
# vykreslení výsledku
plt.scatter(x, y, color="black", s=2)
plt.plot(x, y_pred, color="blue", linewidth=2)
# titulek grafu
plt.title("Linear regression")
# osy
plt.xticks()
plt.yticks()
# ulozeni diagramu do souboru
plt.savefig("114.png")
# zobrazeni diagramu
plt.show()
Výsledky mohou vypadat následovně.
Nesymetrický případ:
X shape: (50, 1) y shape: (50,) Coefficients: [0.23191679] Intercept: 0.0
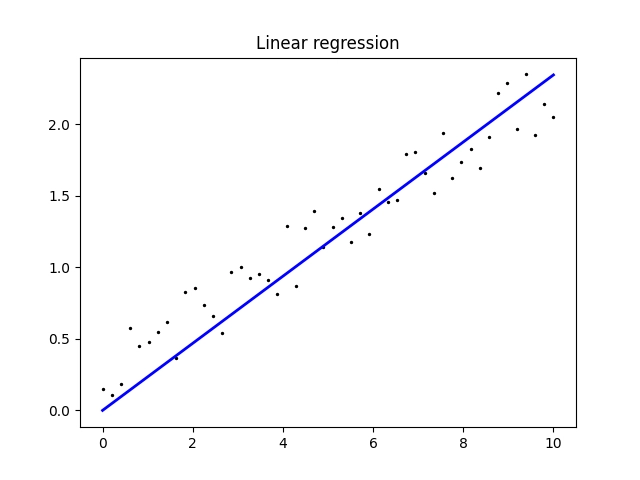
Obrázek 4: Nesymetrický případ.
Symetrický případ:
X shape: (50, 1) y shape: (50,) Coefficients: [0.19996755] Intercept: 0.0
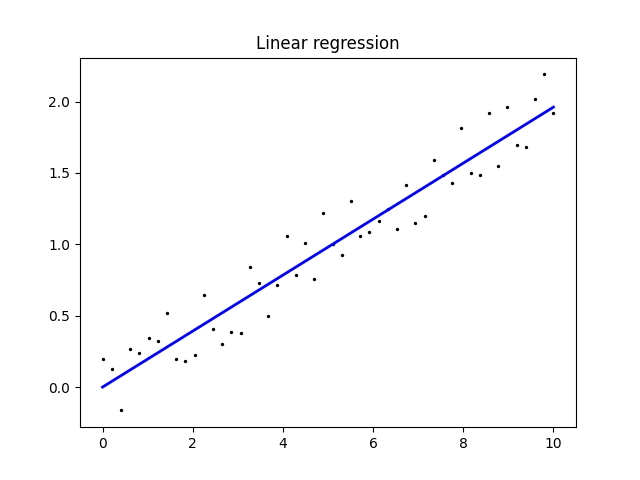
Obrázek 5: Symetrický případ.
6. Model lineární regrese pro větší množství předpovídaných hodnot
Předchozí trojice demonstračních příkladů ukazovala to nejjednodušší použití modelu lineární regrese, konkrétně případ, kdy vstupními hodnotami (atributy, proměnnými) je jednorozměrný vektor a pro každou vstupní hodnotu dostaneme jedinou hodnotu výstupní. Ovšem model lineární regrese je ve skutečnosti mnohem univerzálnější, což si ostatně ukážeme v navazujících kapitolách. Nejdříve si ukážeme, jak dokáže model lineární regrese předpovídat větší množství hodnot. Technicky to znamená, že y (očekávané, resp. predikované hodnoty) již nebude jednorozměrným vektorem, ale dvourozměrnou maticí, přičemž počet sloupců této matice odpovídá počtu předpovídaných hodnot.
7. Model předpovídající pro každou vstupní hodnotu dvě výstupní hodnoty (odpovědi)
Vyzkoušejme si nyní zkonstruovat model, který na základě jediné vstupní hodnoty předpoví dvě výstupní hodnoty (tedy odpovědi). Model tedy budeme muset natrénovat tak, že mu namísto vektoru y předáme matici Y obsahující dva sloupce očekávaných odpovědí. Například:
# Y je matice vytvořená ze dvou vektorů y1 = np.linspace(-1, 1, VALUES) + 0.5*np.random.rand(VALUES) y2 = np.linspace(1, -1, VALUES) + 0.5*np.random.rand(VALUES) # konstrukce matice se dvěma sloupci Y= np.column_stack((y1, y2))
Skript po svém spuštění vypíše parametry obou přímek a samozřejmě provede vizualizaci do dvou nezávislých grafů:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# počet vzorků ve vektorech x i y
VALUES = 50
# x je vektor
x = np.linspace(0, 10, VALUES)
# Y je matice vytvořená ze dvou vektorů
y1 = np.linspace(-1, 1, VALUES) + 0.5*np.random.rand(VALUES)
y2 = np.linspace(1, -1, VALUES) + 0.5*np.random.rand(VALUES)
# konstrukce matice se dvěma sloupci
Y= np.column_stack((y1, y2))
# převod vektoru na 2D matici
X = x.reshape(-1, 1)
# tvar matic X a Y
print("X shape:", X.shape)
print("Y shape:", Y.shape)
# konstrukce modelu
lr = linear_model.LinearRegression()
# trénink modelu
lr.fit(X, Y)
# predikce modelu
y_pred = lr.predict(X)
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", lr.coef_)
print("Intercept: \n", lr.intercept_)
for dimension in range(0, 2):
# vykreslení výsledku
plt.scatter(x, Y[:, dimension], color="black", s=2)
plt.plot(x, y_pred[:, dimension], color="blue", linewidth=2)
# titulek grafu
plt.title(f"Linear regression in dimension {dimension}")
# osy
plt.xticks()
plt.yticks()
# ulozeni diagramu do souboru
plt.savefig(f"115_{dimension}.png")
# zobrazeni diagramu
plt.show()
# druhy diagram
plt.close()
Vykreslené obrázky přesně odpovídají našim předpokladům, tj. že každá z přímek bude interpolovat jednu sadu bodů:
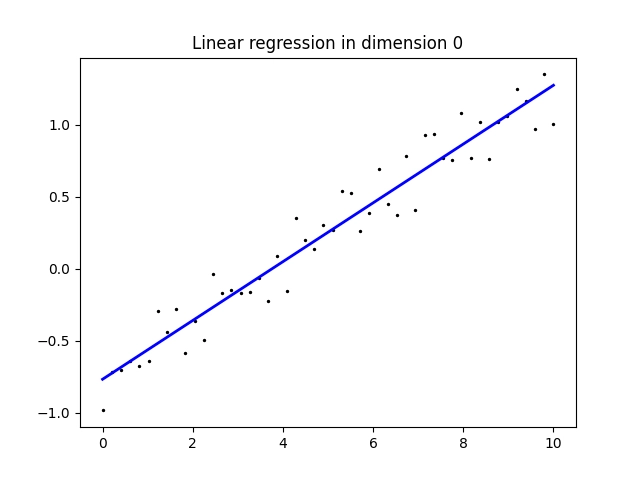
Obrázek 6: Interpolace bodů [x, y1n] přímkou.
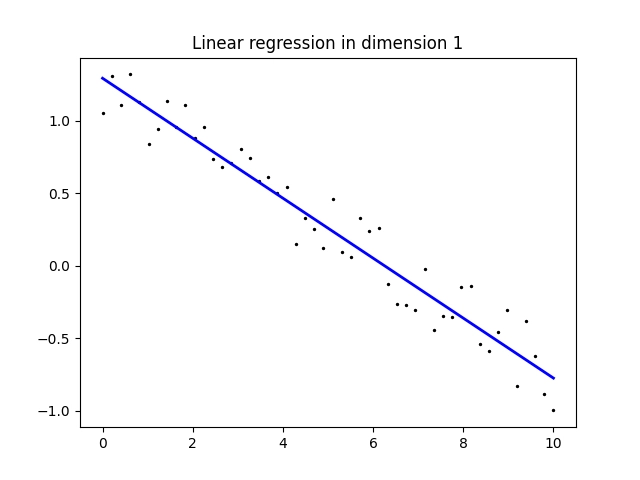
Obrázek 7: Interpolace bodů [x, y2n] odlišnou přímkou.
Je vhodné se podívat i na to, jakým způsobem jsou zobrazeny koeficienty obou přímek. Povšimněte si, že koeficienty nejsou v tomto případě tvořeny vektorem, ale dvourozměrnou maticí (i když tato matice obsahuje dva prvky). Tím odlišíme koeficienty jiného útvaru (roviny atd.) od koeficientů dvou přímek:
X shape: (50, 1) Y shape: (50, 2) Coefficients: [[ 0.20951354] [-0.20570636]] Intercept: [-0.8033512 1.26249794]
Jedná se tedy o dvě přímky s rovnicemi:
y1 = 0.20951354*x - 0,8033512 y2 = -0.20570636*x + 1,26249794
což zhruba odpovídá očekávanému výsledku se směrnicemi 2/10 a –2/10.
8. Lineární regrese a proložení bodů rovinou
Připomeňme si výraz, který model lineární regrese interně používá pro předpovědi prováděné na základě zapamatovaného vektoru w:
y(w, x) = w0 + w1 x1 + w2 x2 + … + wp xp
Ovšem jednotlivé členy nemusí být skalárními hodnotami, ale může se opět jednat o vektory. To vlastně znamená, že jednotlivé hodnoty xn mohou být vícerozměrné. V praxi to znamená, že se můžeme pokusit proložit body v prostoru (již ne v rovině). Tentokrát však budeme prokládat nikoli přímkou, ale rovinou. A právě tento postup si ukážeme v navazujících kapitolách. Nejprve si však musíme ukázat (resp. připomenout) některé operace, které lze provádět v knihovně NumPy: vygenerování souřadné mřížky atd.
9. Konstrukce matice obsahující souřadnice bodů v mřížce
Připomeňme si, že pro trénink modelu potřebujeme mít k dispozici matici X, která obsahuje jednotlivé záznamy, na kterých se bude model trénovat. Každý záznam může mít více položek, tj. počet sloupců matice určuje i počet atributů, na kterých se model učí. Pro naši lineární interpolaci rovinou budeme potřebovat vytvořit matici se dvěma sloupci, která bude v prvním sloupci obsahovat x-ové souřadnice bodů a ve druhém sloupci souřadnice y-ové. Takovou matici můžeme vytvořit transformací matic s mřížkou souřadnic – jedna matice obsahuje x-ové souřadnice v mřížce, druhá matice souřadnice y-ové (výsledek operace meshgrid). Tyto matice „zploštíme“ do dvojice vektorů a dva výsledné vektory spojíme do nové dvourozměrné matice se dvěma sloupci. Zní to složitě? Podívejme se na celý postup:
import numpy as np
# počet vzorků v mřížce
VALUES = 5
# X je matice vytvořená z mřížky
# dvojice vektorů pro konstrukci mřížky
x1 = np.linspace(0, 100, VALUES)
x2 = np.linspace(0, 100, VALUES)
print("x1:", x1)
print("x2:", x2)
print()
# konstrukce mřížky
grid = np.meshgrid(x1, x2)
print("grid #1:\n", grid[0])
print()
print("grid #2:\n", grid[1])
print()
# změna tvaru na matici se dvěma sloupci
X = np.vstack([grid[0].flatten(), grid[1].flatten()]).T
print("X shape:", X.shape)
print(X)
print()
# y je vektor
y = (grid[0] + grid[1]).flatten()
print("y shape:", y.shape)
print(y)
Jednotlivé kroky budou více pochopitelné při pohledu na výstup skriptu.
Vstupní vektory x1 a x2 s hodnotami na osách souřadného systému:
x1: [ 0. 25. 50. 75. 100.] x2: [ 0. 25. 50. 75. 100.]
Operací meshgrid vzniknou dvě matice, první s x1-ovými body v mřížce, druhá s body x2-ovými:
grid #1: [[ 0. 25. 50. 75. 100.] [ 0. 25. 50. 75. 100.] [ 0. 25. 50. 75. 100.] [ 0. 25. 50. 75. 100.] [ 0. 25. 50. 75. 100.]] grid #2: [[ 0. 0. 0. 0. 0.] [ 25. 25. 25. 25. 25.] [ 50. 50. 50. 50. 50.] [ 75. 75. 75. 75. 75.] [100. 100. 100. 100. 100.]]
Po zploštění těchto matic do vektorů a spojení vektorů do matice dostaneme matici, v níž každý řádek obsahuje souřadnice v prvních dvou souřadných osách:
X shape: (25, 2) [[ 0. 0.] [ 25. 0.] [ 50. 0.] [ 75. 0.] [100. 0.] [ 0. 25.] [ 25. 25.] [ 50. 25.] [ 75. 25.] [100. 25.] [ 0. 50.] [ 25. 50.] [ 50. 50.] [ 75. 50.] [100. 50.] [ 0. 75.] [ 25. 75.] [ 50. 75.] [ 75. 75.] [100. 75.] [ 0. 100.] [ 25. 100.] [ 50. 100.] [ 75. 100.] [100. 100.]]
A vektor y obsahuje souřadnice bodů ve třetí ose:
y shape: (25,) [ 0. 25. 50. 75. 100. 25. 50. 75. 100. 125. 50. 75. 100. 125. 150. 75. 100. 125. 150. 175. 100. 125. 150. 175. 200.]
10. Proložení bodů v prostoru rovinou
Nyní se již můžeme pokusit o proložení bodů, které leží v trojrozměrném prostoru, rovinou. x-ové a y-ové souřadnice bodů tvoří pravidelnou mřížku, z-ová souřadnice se mění podle zadaného vzorce (a později se bude měnit náhodně, resp. pseudonáhodně). Následně natrénujeme model takovým způsobem, aby tyto body proložil rovinou:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# počet vzorků v mřížce
VALUES = 20
# X je matice vytvořená z mřížky
# dvojice vektorů pro konstrukci mřížky
x1 = np.linspace(1, 100, VALUES)
x2 = np.linspace(1, 100, VALUES)
# konstrukce mřížky
grid = np.meshgrid(x1, x2)
# změna tvaru na matici se dvěma sloupci
X = np.vstack([grid[0].flatten(), grid[1].flatten()]).T
# y je vektor
y = (grid[0] + grid[1]).flatten()
# tvar matice X a vektoru y
print("X shape:", X.shape)
print("y shape:", y.shape)
# konstrukce modelu
lr = linear_model.LinearRegression()
# trénink modelu
lr.fit(X, y)
# predikce modelu
y_pred = lr.predict(X).reshape((VALUES, VALUES))
print(y_pred)
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", lr.coef_)
print("Intercept: \n", lr.intercept_)
# vykreslení výsledku do 3D grafu
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(projection='3d')
# body ze vstupní datové sady
ax.scatter(X[:, 0], X[:, 1], y, color="black", s=2)
# výsledkem modelu je rovina
ax.plot_surface(grid[0], grid[1], y_pred, alpha = 0.5)
# ulozeni diagramu do souboru
plt.savefig("117_.png")
# zobrazeni diagramu
plt.show()
Podívejme se na výsledky:
Coefficients: [1. 1.] Intercept: -2.842170943040401e-14
Koeficienty jsou uloženy jako jednorozměrné pole a tedy představují rovnici roviny ve tvaru:
z = 1x + 1y - 2.84...
ovšem posun je prakticky nulový:
z = x + y
Vizuálně vypadá výsledek následovně:
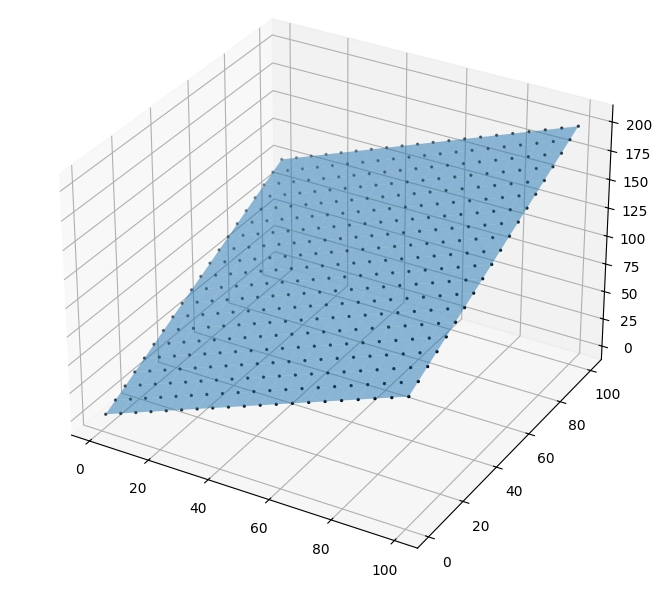
Obrázek 8: Výchozí pohled.
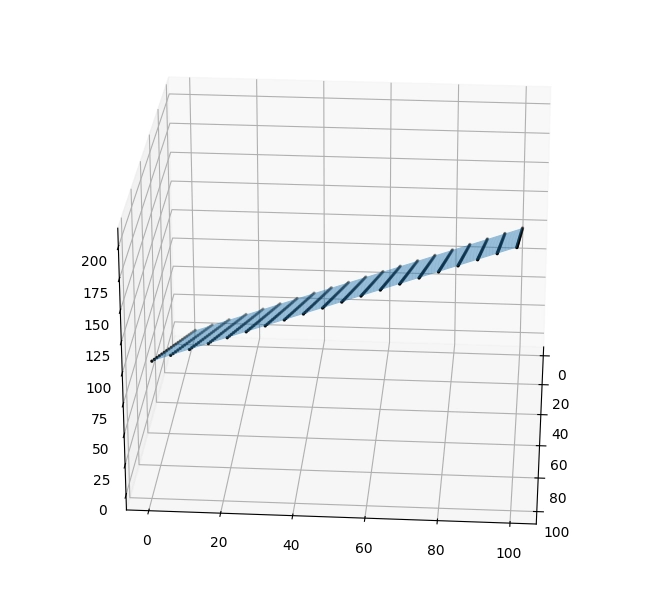
Obrázek 9: Pohled zboku – skutečně se jedná o rovinu.
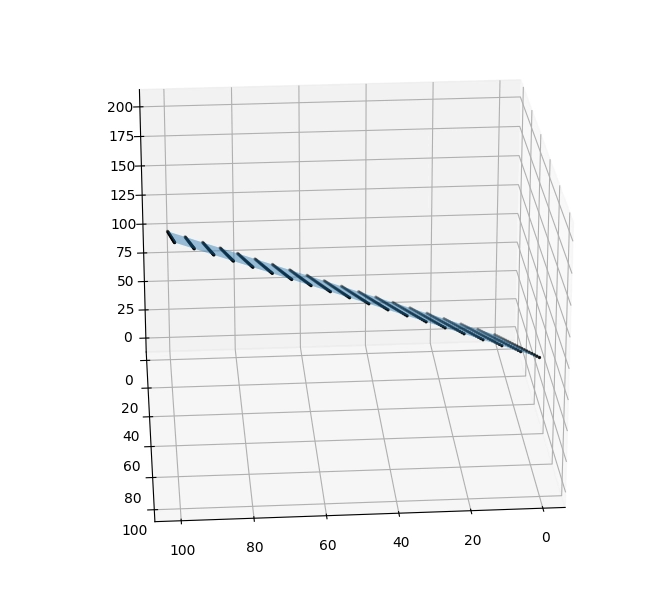
Obrázek 10: Pohled z jiného boku – skutečně se jedná o rovinu.

Obrázek 11: Půdorysný pohled ukazující, jak tvoří body pravidelnou mřížku v rovině x-y.
11. Proložení rovinou při přidání náhodnosti do pozic bodů v prostoru
Nyní k výšce bodů přidáme náhodnou hodnotu, takže již všechny body nebudou ležet v jedné rovině:
# y je vektor y = (grid[0] + grid[1]).flatten() + 50*np.random.rand(VALUES**2)
Znovu provedeme stejné operace, jako tomu bylo v předchozí kapitole; včetně zobrazení proložení bodů rovinou:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# počet vzorků v mřížce
VALUES = 20
# X je matice vytvořená z mřížky
# dvojice vektorů pro konstrukci mřížky
x1 = np.linspace(1, 100, VALUES)
x2 = np.linspace(1, 100, VALUES)
# konstrukce mřížky
grid = np.meshgrid(x1, x2)
# změna tvaru na matici se dvěma sloupci
X = np.vstack([grid[0].flatten(), grid[1].flatten()]).T
# y je vektor
y = (grid[0] + grid[1]).flatten() + 50*np.random.rand(VALUES**2)
# tvar matice X a vektoru y
print("X shape:", X.shape)
print("y shape:", y.shape)
# konstrukce modelu
lr = linear_model.LinearRegression()
# trénink modelu
lr.fit(X, y)
# predikce modelu
y_pred = lr.predict(X).reshape((VALUES, VALUES))
print(y_pred)
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", lr.coef_)
print("Intercept: \n", lr.intercept_)
# vykreslení výsledku do 3D grafu
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(projection='3d')
# body ze vstupní datové sady
ax.scatter(X[:, 0], X[:, 1], y, color="black", s=2)
# výsledkem modelu je rovina
ax.plot_surface(grid[0], grid[1], y_pred, alpha = 0.5)
# ulozeni diagramu do souboru
plt.savefig("118_.png")
# zobrazeni diagramu
plt.show()
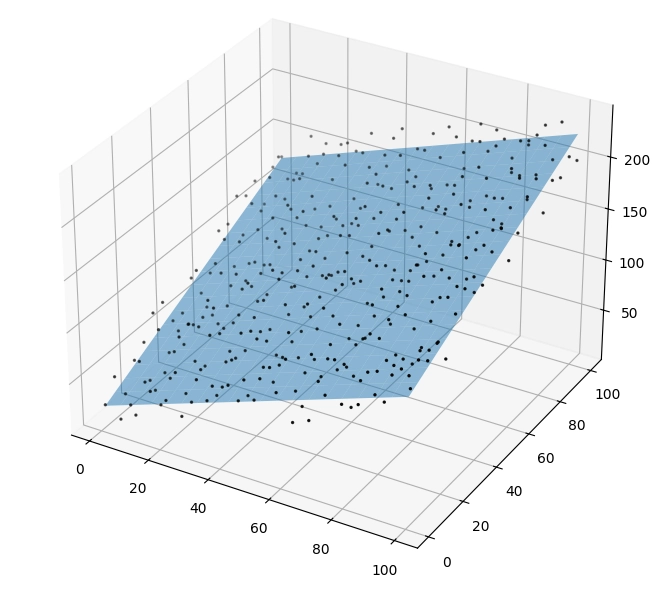
Obrázek 12: Výchozí pohled.
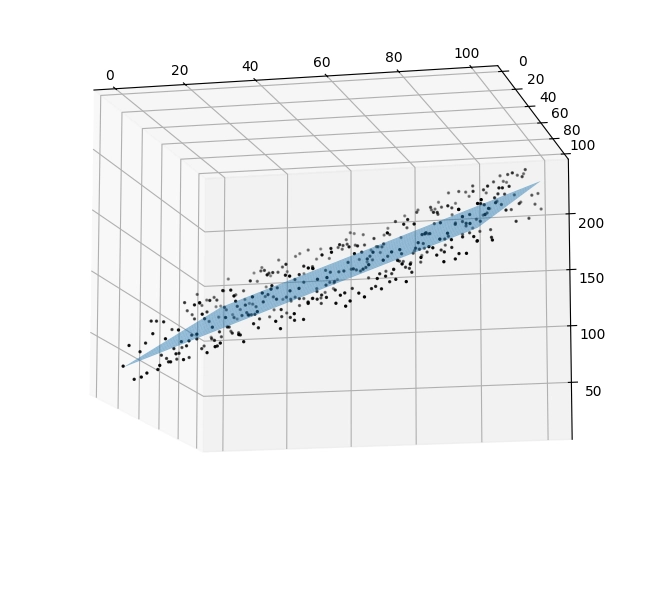
Obrázek 13: Pohled zboku – skutečně se jedná o rovinu, ovšem body jsou umístěny okolo ní, nikoli přímo na rovině.
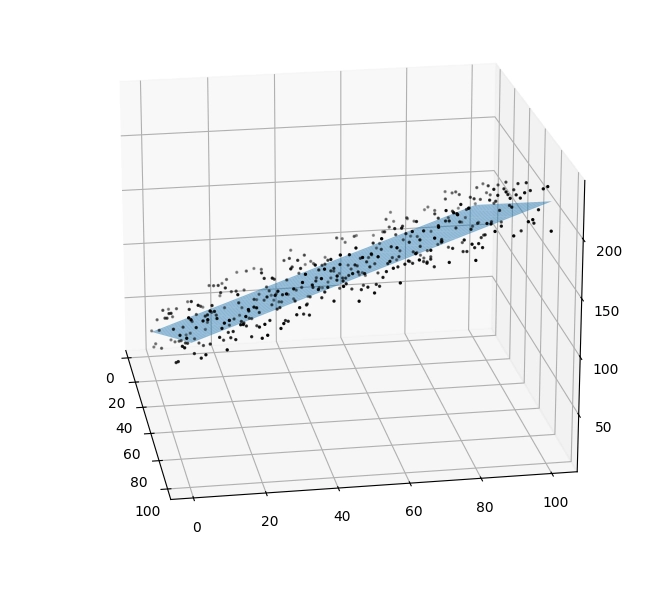
Obrázek 14: Pohled z jiného boku – skutečně se jedná o rovinu.
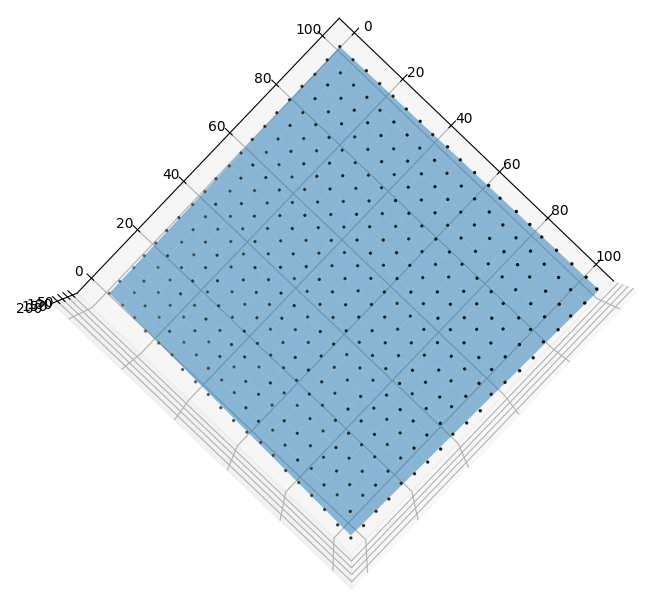
Obrázek 15: Pohled ukazující, jak tvoří body pravidelnou mřížku v rovině x-y.
12. Kombinace předchozích příkladů: přechod z roviny do prostoru a více sad očekávaných výsledků
V předchozích demonstračních příkladech jsme si ukázali dvě možnosti poskytované modelem pro provádění lineární regrese. Jednalo se o přechod z roviny (známé hodnoty x, neznámé hodnoty y) do prostoru (známé hodnoty [x, y], neznámé hodnoty z) a taktéž o podporu více „sloupců“ neznámých hodnot, což znamená, že model bylo možné natrénovat tak, že interně obsahoval informace o několika přímkách, každou pro jiný sloupec neznámých hodnot. Nyní oba tyto koncepty v rámci dalšího textu zkombinujeme a ukážeme si, jak lze realizovat trénink modelu, který bude prokládat dvě sady bodů v prostoru, a to pochopitelně nikoli přímkami, ale rovinami. I tím se ukazuje všestrannost a univerzálnost zdánlivě triviálního modelu pro lineární regresi.
13. Proložení dvou sad bodů dvěma nezávislými rovinami
Jak bylo řečeno v předchozí kapitole, ukážeme si proložení dvou sad bodů (v prostoru) dvěma nezávislými rovinami. Zajímat nás bude jak vizuální výsledek, tak i způsob uložení koeficientů těchto dvou rovin v interní paměti (atributech) modelu.
Obě sady bodů budou mít stejné x-ové a y-ové souřadnice tvořící (po projekci do roviny x-y) pravidelnou mřížku:
# X je matice vytvořená z mřížky # dvojice vektorů pro konstrukci mřížky x1 = np.linspace(1, 100, VALUES) x2 = np.linspace(1, 100, VALUES) # konstrukce mřížky grid = np.meshgrid(x1, x2) # změna tvaru na matici se dvěma sloupci X = np.vstack([grid[0].flatten(), grid[1].flatten()]).T
z-ové souřadnice bodů (zde ukládané do matice pojmenované Y, což je možná poněkud matoucí) budou nezávislé a budou tvořit dva sloupce hodnot, na které se model trénuje:
# Y je matice vytvořená ze dvou vektorů y1 = (grid[0] + grid[1]).flatten() + 0*np.random.rand(VALUES**2) y2 = (grid[0] - grid[1]).flatten() + 0*np.random.rand(VALUES**2) # konstrukce matice se dvěma sloupci Y= np.column_stack((y1, y2))
Celý skript, i s vykreslením příslušné dvojice diagramů, vypadá následovně:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# počet vzorků v mřížce
VALUES = 20
# X je matice vytvořená z mřížky
# dvojice vektorů pro konstrukci mřížky
x1 = np.linspace(1, 100, VALUES)
x2 = np.linspace(1, 100, VALUES)
# konstrukce mřížky
grid = np.meshgrid(x1, x2)
# změna tvaru na matici se dvěma sloupci
X = np.vstack([grid[0].flatten(), grid[1].flatten()]).T
# Y je matice vytvořená ze dvou vektorů
y1 = (grid[0] + grid[1]).flatten() + 0*np.random.rand(VALUES**2)
y2 = (grid[0] - grid[1]).flatten() + 0*np.random.rand(VALUES**2)
# konstrukce matice se dvěma sloupci
Y= np.column_stack((y1, y2))
# tvar matic X a Y
print("X shape:", X.shape)
print("Y shape:", Y.shape)
# konstrukce modelu
lr = linear_model.LinearRegression()
# trénink modelu
lr.fit(X, Y)
# predikce modelu
y_pred = lr.predict(X).reshape((VALUES, VALUES, 2))
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", lr.coef_)
print("Intercept: \n", lr.intercept_)
for dimension in range(0, 2):
# vykreslení výsledku do 3D grafu
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(projection='3d')
# body ze vstupní datové sady
ax.scatter(X[:, 0], X[:, 1], Y[:, dimension], color="black", s=2)
# výsledkem modelu je rovina
ax.plot_surface(grid[0], grid[1], y_pred[:, :, dimension], alpha = 0.5)
# ulozeni diagramu do souboru
plt.savefig(f"119_{dimension}.png")
# zobrazeni diagramu
plt.show()
Podívejme se nejdříve na hodnoty, které model získal tréninkem:
X shape: (400, 2) Y shape: (400, 2) Coefficients: [[ 1. 1.] [ 1. -1.]] Intercept: [-2.84217094e-14 -3.25739435e-14]
Koeficienty tvoří matici 2×2 hodnoty, z nichž lze odvodit rovnice dvou rovin:
z1 = 1x + 1y = x + y z2 = 1x - 1y = x - y
To přesně odpovídá tomu, jak jsme body generovali.
Vizuální výsledek naznačuje orientaci a posun obou rovin v prostoru:
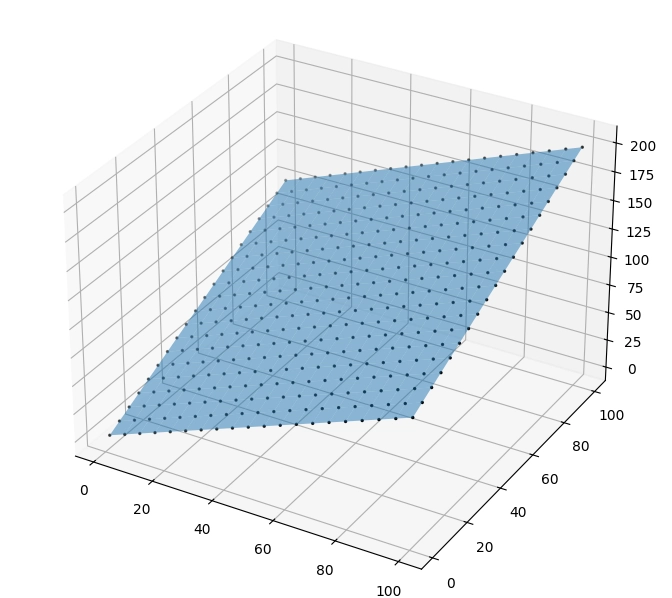
Obrázek 16: Orientace a posun první roviny.
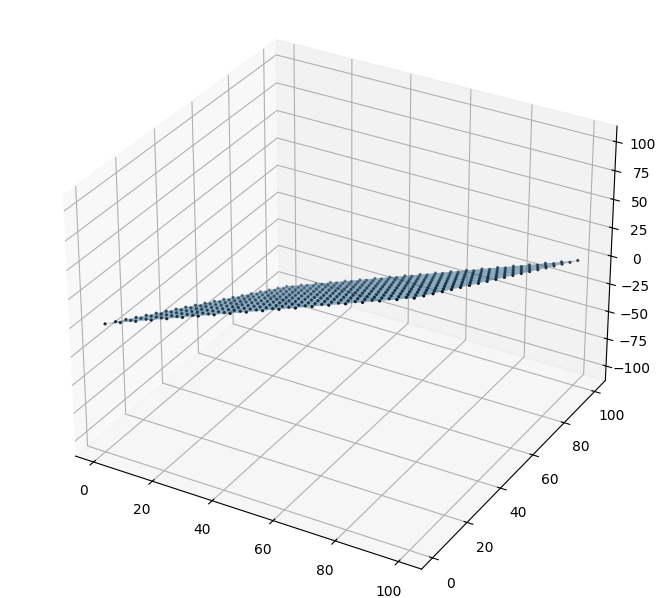
Obrázek 17: Orientace a posun druhé roviny.
14. Přidání náhodné výšky bodů v datové sadě
V dalším kroku skript z předchozí kapitoly nepatrně upravíme, a to takovým způsobem, že body z obou sad posuneme o náhodnou hodnotu (pro jednoduchost jen ve směru osy z):
# Y je matice vytvořená ze dvou vektorů y1 = (grid[0] + grid[1]).flatten() + 50*np.random.rand(VALUES**2) y2 = (grid[0] - grid[1]).flatten() + 50*np.random.rand(VALUES**2) # konstrukce matice se dvěma sloupci Y= np.column_stack((y1, y2))
Úplný zdrojový kód takto upraveného skriptu bude vypadat následovně:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# počet vzorků v mřížce
VALUES = 20
# X je matice vytvořená z mřížky
# dvojice vektorů pro konstrukci mřížky
x1 = np.linspace(1, 100, VALUES)
x2 = np.linspace(1, 100, VALUES)
# konstrukce mřížky
grid = np.meshgrid(x1, x2)
# změna tvaru na matici se dvěma sloupci
X = np.vstack([grid[0].flatten(), grid[1].flatten()]).T
# Y je matice vytvořená ze dvou vektorů
y1 = (grid[0] + grid[1]).flatten() + 50*np.random.rand(VALUES**2)
y2 = (grid[0] - grid[1]).flatten() + 50*np.random.rand(VALUES**2)
# konstrukce matice se dvěma sloupci
Y= np.column_stack((y1, y2))
# tvar matic X a Y
print("X shape:", X.shape)
print("Y shape:", Y.shape)
# konstrukce modelu
lr = linear_model.LinearRegression()
# trénink modelu
lr.fit(X, Y)
# predikce modelu
y_pred = lr.predict(X).reshape((VALUES, VALUES, 2))
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", lr.coef_)
print("Intercept: \n", lr.intercept_)
for dimension in range(0, 2):
# vykreslení výsledku do 3D grafu
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(projection='3d')
# body ze vstupní datové sady
ax.scatter(X[:, 0], X[:, 1], Y[:, dimension], color="black", s=2)
# výsledkem modelu je rovina
ax.plot_surface(grid[0], grid[1], y_pred[:, :, dimension], alpha = 0.5)
# ulozeni diagramu do souboru
plt.savefig(f"120_{dimension}.png")
# zobrazeni diagramu
plt.show()
Vizuální výsledky ukazují, že model skutečně dokázal proložit i (pseudo)náhodně rozmístěné body pomocí přímek:
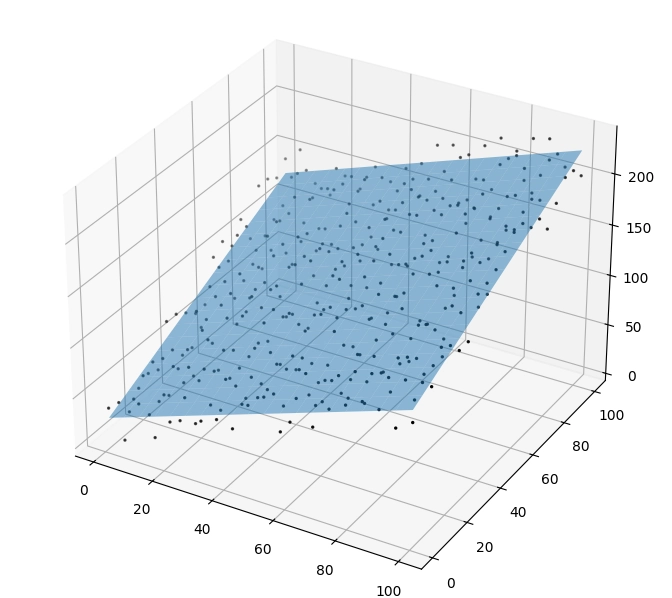
Obrázek 18: Orientace a posun první roviny prokládající (pseudo)náhodně uspořádané body.
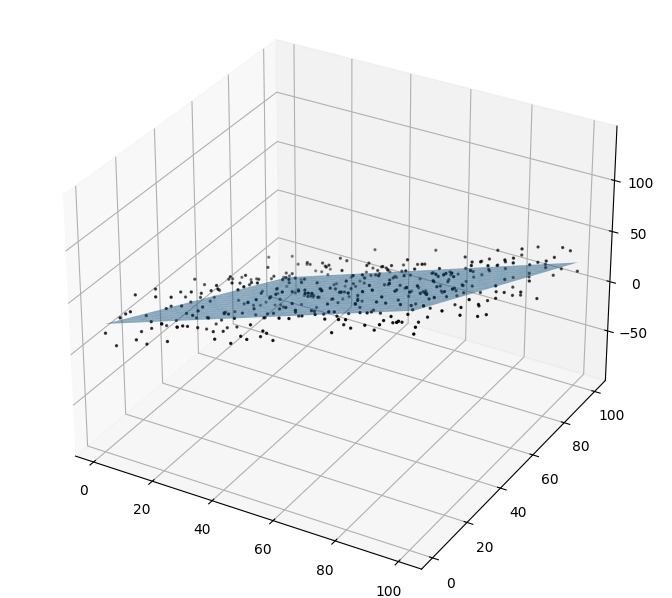
Obrázek 19: Orientace a posun druhé roviny prokládající (pseudo)náhodně uspořádané body.
15. Polynomická regrese
V mnoha případech je namísto modelu s interní lineární závislostí (nebo, jak již víme, s více lineárními závislostmi) mezi vstupními daty a očekávanými výsledky výhodnější použít polynom, resp. polynomy vyššího stupně. I to nám knihovna scikit-learn umožňuje, a to z toho důvodu, že model pro lineární regresi může být natrénován tak, že odvodí parametry polynomu/polynomů – z hlediska modelu totiž není rozdíl mezi vstupními daty, které prokládá lineárním objektem a parametry (polynomu), které opět prokládá tak, že volí váhy jednotlivých členů. Ovšem podobným způsobem lze zajistit například proložení dat sinusovkou atd.
16. Příklad jednoduché polynomické regrese
Podívejme se nyní – opět jen pro zopakování – na příklad realizace polynomické regrese, konkrétně pro proložení bodů v rovině křivkou určenou polynomem druhého stupně, jinými slovy parabolou. Model se tedy bude snažit o nalezení vah členů polynomu tak, aby průměr čtverců chyb byl co nejmenší:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.preprocessing import PolynomialFeatures
# počet vzorků ve vektorech x i y (delitelne tremi)
VALUES = 120
# x je vektor
x = np.linspace(0, 10, VALUES)
# mensi vektory pro slozeni y
y1 = 0.5*np.random.rand(VALUES//3)
y2 = 1 + 0.5*np.random.rand(VALUES//3)
y3 = 0.5*np.random.rand(VALUES//3)
# y je vektor
y = np.concatenate((y1, y2, y3))
# převod vektoru na 2D matici
X = x.reshape(-1, 1)
# tvar matice X a vektoru y
print("X shape:", X.shape)
print("y shape:", y.shape)
degree = 2
# konstrukce modelu
pr = linear_model.LinearRegression(fit_intercept=False)
poly = PolynomialFeatures(degree=degree)
poly_features = poly.fit_transform(X)
# trénink modelu (X musí být maticí)
pr.fit(poly_features, y)
# predikce modelu
y_pred = pr.predict(poly_features)
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", pr.coef_)
print("Intercept: \n", pr.intercept_)
# vykreslení výsledku
plt.scatter(x, y, color="black", s=2)
plt.plot(x, y_pred, color="blue", linewidth=2)
# titulek grafu
plt.title(f"Degree={degree}")
# osy
plt.xticks(())
plt.yticks(())
# ulozeni diagramu do souboru
plt.savefig("121.png")
# zobrazeni diagramu
plt.show()
Výsledek by měl vypadat následovně – křivka je zvolena takovým způsobem, aby byla chyba co nejmenší:
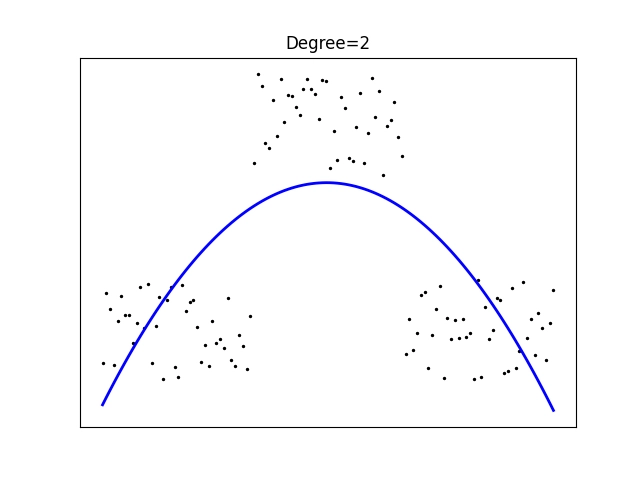
Obrázek 20: Aproximace polynomem druhého stupně.
Koeficienty paraboly:
Coefficients: [-0.12242606 0.43023016 -0.04299919] Intercept: 0.0
17. Proložení bodů v prostoru plochou prvního stupně (rovinou)
Nyní si skript z předchozí kapitoly rozšíříme takovým způsobem, že proložíme body v prostoru (nikoli již v rovině) plochou n-tého stupně, tedy rovinou (to již známe), paraboloidem atd. Nejprve začneme běžnou rovinou, kterou se budeme snažit proložit body, které leží na sedlové ploše (což zajisté není rovina):
degree = 1 poly = PolynomialFeatures(degree=degree)
Celý skript:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.preprocessing import PolynomialFeatures
# počet vzorků v mřížce
VALUES = 20
# X je matice vytvořená z mřížky
# dvojice vektorů pro konstrukci mřížky
x1 = np.linspace(1, 100, VALUES)
x2 = np.linspace(1, 100, VALUES)
# konstrukce mřížky
grid = np.meshgrid(x1, x2)
# změna tvaru na matici se dvěma sloupci
X = np.vstack([grid[0].flatten(), grid[1].flatten()]).T
# y je vektor
y = ((grid[0]-50) * (grid[1]-50)).flatten()
# tvar matice X a vektoru y
print("X shape:", X.shape)
print("y shape:", y.shape)
degree = 1
# konstrukce modelu
pr = linear_model.LinearRegression()
poly = PolynomialFeatures(degree=degree)
poly_features = poly.fit_transform(X)
# trénink modelu
pr.fit(poly_features, y)
# predikce modelu
y_pred = pr.predict(poly_features).reshape((VALUES, VALUES))
print(y_pred)
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", pr.coef_)
print("Intercept: \n", pr.intercept_)
# vykreslení výsledku do 3D grafu
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(projection='3d')
# body ze vstupní datové sady
ax.scatter(X[:, 0], X[:, 1], y, color="black", s=2)
# výsledkem modelu je rovina
ax.plot_surface(grid[0], grid[1], y_pred, alpha = 0.5)
# ulozeni diagramu do souboru
plt.savefig("122.png")
# zobrazeni diagramu
plt.show()
Výsledek nebude příliš dobrý, což jsme ovšem očekávali:
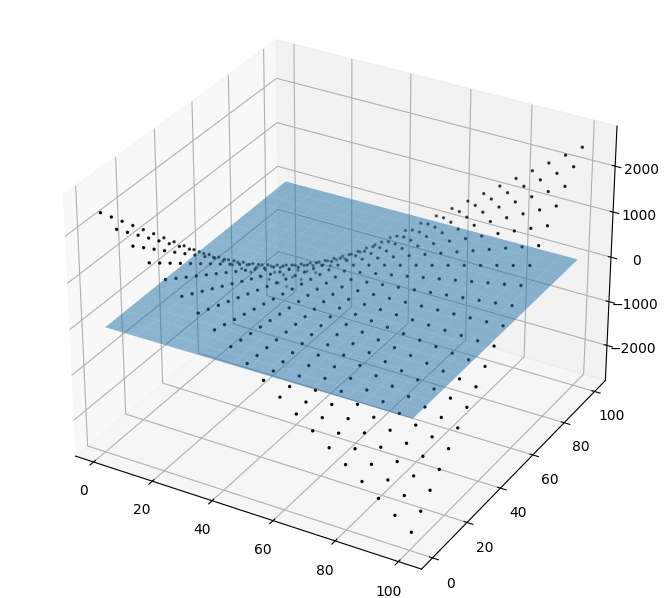
Obrázek 21: Pokus o proložení bodů, které ve skutečnosti leží na sedlové ploše, rovinou.
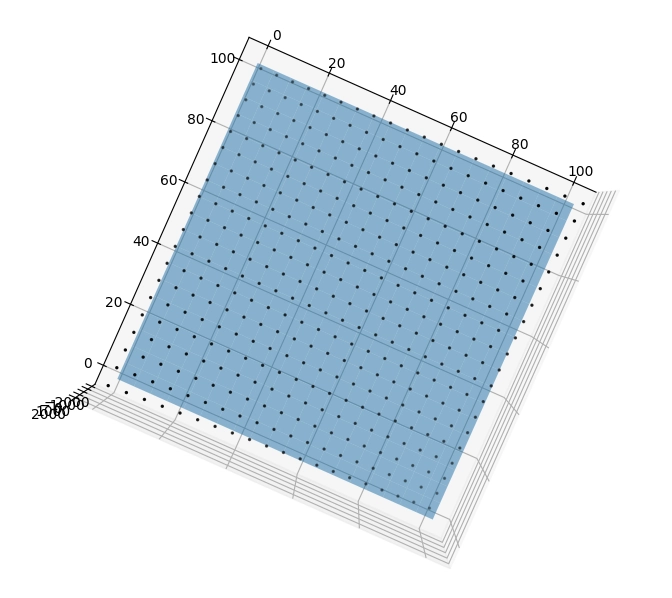
Obrázek 22: Půdorysný pohled.
18. Proložení bodů v prostoru plochou druhého stupně
Aby byl výsledek uspokojující, použijeme plochu druhého stupně:
degree = 2 poly = PolynomialFeatures(degree=degree)
Celý skript vypadá následovně:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.preprocessing import PolynomialFeatures
# počet vzorků v mřížce
VALUES = 20
# X je matice vytvořená z mřížky
# dvojice vektorů pro konstrukci mřížky
x1 = np.linspace(1, 100, VALUES)
x2 = np.linspace(1, 100, VALUES)
# konstrukce mřížky
grid = np.meshgrid(x1, x2)
# změna tvaru na matici se dvěma sloupci
X = np.vstack([grid[0].flatten(), grid[1].flatten()]).T
# y je vektor
y = ((grid[0]-50) * (grid[1]-50)).flatten()
# tvar matice X a vektoru y
print("X shape:", X.shape)
print("y shape:", y.shape)
degree = 2
# konstrukce modelu
pr = linear_model.LinearRegression()
poly = PolynomialFeatures(degree=degree)
poly_features = poly.fit_transform(X)
# trénink modelu
pr.fit(poly_features, y)
# predikce modelu
y_pred = pr.predict(poly_features).reshape((VALUES, VALUES))
print(y_pred)
# výpis vypočtených koeficientů modelu
print("Coefficients: \n", pr.coef_)
print("Intercept: \n", pr.intercept_)
# vykreslení výsledku do 3D grafu
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(projection='3d')
# body ze vstupní datové sady
ax.scatter(X[:, 0], X[:, 1], y, color="black", s=2)
# výsledkem modelu je rovina
ax.plot_surface(grid[0], grid[1], y_pred, alpha = 0.5)
# ulozeni diagramu do souboru
plt.savefig("123.png")
# zobrazeni diagramu
plt.show()
Nyní již budou výsledky mnohem lepší (ideální):
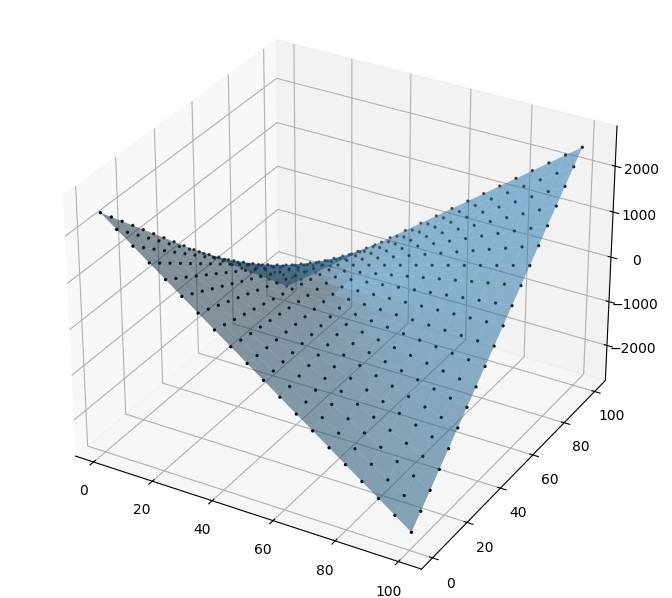
Obrázek 23: Proložení bodů plochou druhého stupně.
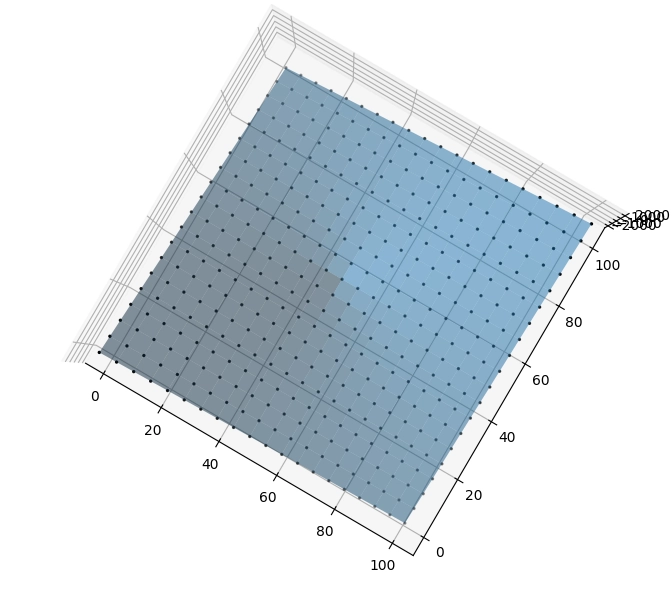
Obrázek 24: Proložení bodů plochou druhého stupně.
Koeficienty určují váhy členů plochy určené polynomy druhého stupně:
Coefficients: [ 0.00000000e+00 -5.00000000e+01 -5.00000000e+01 3.55271368e-15 1.00000000e+00 2.84217094e-14] Intercept: 2500.0000000000223
Přitom váhy jsou zapsány v pořadí:
y(w, x) = w0 + w1 x1 + w2 x2 + w3 x12 + w4 x1 x2 + w5 x22
Což po zaokrouhlení a dosazení odpovídá ploše:
y(w, x) = 2500 -50x1 - 50x2 + x1x2
19. Repositář s demonstračními příklady
Všechny demonstrační příklady využívající knihovnu Scikit-learn lze nalézt v repositáři https://github.com/tisnik/most-popular-python-libs. Následují odkazy na jednotlivé příklady i na (Jupyter) diáře s postupem výpočtů a analýz:
V repositáři nalezneme taktéž projektový soubor a Jupyter Notebook s vysvětlením, jak lze modely využít pro rozpoznávání obsahu rastrových obrázků:
| # | Příklad | Stručný popis | Adresa příkladu |
|---|---|---|---|
| 1 | pyproject.toml | projektový soubor (pro PDM) se všemi závislostmi | https://github.com/tisnik/most-popular-python-libs/blob/master/sklearn/pyproject.toml |
| 2 | pdm.lock | lock soubor s konkrétními verzemi všech přímých i tranzitivních závislostí | https://github.com/tisnik/most-popular-python-libs/blob/master/sklearn/pdm.lock |
| 3 | Rozpoznání_obrazu_scikit-learn.ipynb | Jupyter notebook s celým postupem | https://github.com/tisnik/most-popular-python-libs/blob/master/sklearn/Rozpoznání_obrazu_scikit-learn.ipynb |
| 4 | particle_life.py | emergence: příklad vzniku struktury | https://github.com/tisnik/most-popular-python-libs/blob/master/particles/particle_life.py |
20. Odkazy na Internetu
- Shluková analýza (clustering) a knihovna Scikit-learn
https://www.root.cz/clanky/shlukova-analyza-clustering-a-knihovna-scikit-learn/ - Shluková analýza (clustering) a knihovna Scikit-learn (2)
https://www.root.cz/clanky/shlukova-analyza-clustering-a-knihovna-scikit-learn-2/ - Shluková analýza (clustering) a knihovna Scikit-learn (z plochy do 3D prostoru)
https://www.root.cz/clanky/shlukova-analyza-clustering-a-knihovna-scikit-learn-z-plochy-do-3d-prostoru/ - Rozpoznávání obrázků knihovnou Scikit-learn: první kroky
https://www.root.cz/clanky/rozpoznavani-obrazku-knihovnou-scikit-learn-prvni-kroky/ - scikit-learn: Machine Learning in Python
https://scikit-learn.org/stable/index.html - Sklearn-pandas
https://github.com/scikit-learn-contrib/sklearn-pandas - sklearn-xarray
https://github.com/phausamann/sklearn-xarray/ - Clustering
https://scikit-learn.org/stable/modules/clustering.html - Cluster analysis (Wikipedia)
https://en.wikipedia.org/wiki/Cluster_analysis - Shluková analýza (Wikipedia)
https://cs.wikipedia.org/wiki/Shlukov%C3%A1_anal%C3%BDza - K-means
https://cs.wikipedia.org/wiki/K-means - k-means clustering
https://en.wikipedia.org/wiki/K-means_clustering - Spectral clustering
https://en.wikipedia.org/wiki/Spectral_clustering - Emergence
https://cs.wikipedia.org/wiki/Emergence - Particle Life: Vivid structures from rudimentary rules
https://particle-life.com/ - Hertzsprungův–Russellův diagram
https://cs.wikipedia.org/wiki/Hertzsprung%C5%AFv%E2%80%93Russell%C5%AFv_diagram - Using Machine Learning in an HR Diagram
https://cocalc.com/share/public_paths/08b6e03583cbdef3cdb9813a54ec68ff773c747f - Gaia H-R diagrams: Querying Gaia data for one million nearby stars
https://vlas.dev/post/gaia-dr2-hrd/ - The Hertzsprung–Russell diagram
https://scipython.com/book2/chapter-9-data-analysis-with-pandas/problems/p92/the-hertzsprung-russell-diagram/ - Animated Hertzsprung-Russell Diagram with 119,614 datapoints
https://github.com/zonination/h-r-diagram - Neuraxle Pipelines
https://github.com/Neuraxio/Neuraxle - scikit-learn: Getting Started
https://scikit-learn.org/stable/getting_started.html - Support Vector Machines
https://scikit-learn.org/stable/modules/svm.html - Use Deep Learning to Detect Programming Languages
http://searene.me/2017/11/26/use-neural-networks-to-detect-programming-languages/ - Natural-language processing
https://en.wikipedia.org/wiki/Natural-language_processing - THE MNIST DATABASE of handwritten digits
http://yann.lecun.com/exdb/mnist/ - MNIST database (Wikipedia)
https://en.wikipedia.org/wiki/MNIST_database - MNIST For ML Beginners
https://www.tensorflow.org/get_started/mnist/beginners - Stránka projektu Torch
http://torch.ch/ - Torch: Serialization
https://github.com/torch/torch7/blob/master/doc/serialization.md - Torch: modul image
https://github.com/torch/image/blob/master/README.md - Data pro neuronové sítě
http://archive.ics.uci.edu/ml/index.php - Torch na GitHubu (několik repositářů)
https://github.com/torch - Torch (machine learning), Wikipedia
https://en.wikipedia.org/wiki/Torch_%28machine_learning%29 - Torch Package Reference Manual
https://github.com/torch/torch7/blob/master/README.md - Torch Cheatsheet
https://github.com/torch/torch7/wiki/Cheatsheet - Neural network containres (Torch)
https://github.com/torch/nn/blob/master/doc/containers.md - Simple layers
https://github.com/torch/nn/blob/master/doc/simple.md#nn.Linear - Transfer Function Layers
https://github.com/torch/nn/blob/master/doc/transfer.md#nn.transfer.dok - Feedforward neural network
https://en.wikipedia.org/wiki/Feedforward_neural_network - Biologické algoritmy (4) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-4-neuronove-site/ - Biologické algoritmy (5) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-5-neuronove-site/ - Umělá neuronová síť (Wikipedia)
https://cs.wikipedia.org/wiki/Um%C4%9Bl%C3%A1_neuronov%C3%A1_s%C3%AD%C5%A5 - PyTorch
http://pytorch.org/ - JupyterLite na PyPi
https://pypi.org/project/jupyterlite/ - JupyterLite na GitHubu
https://github.com/jupyterlite/jupyterlite - Dokumentace k projektu JupyterLite
https://github.com/jupyterlite/jupyterlite - Matplotlib Home Page
http://matplotlib.org/ - Matplotlib (Wikipedia)
https://en.wikipedia.org/wiki/Matplotlib - Popis barvových map modulu matplotlib.cm
https://gist.github.com/endolith/2719900#id7 - Ukázky (palety) barvových map modulu matplotlib.cm
http://matplotlib.org/examples/color/colormaps_reference.html - Galerie grafů vytvořených v Matplotlibu
https://matplotlib.org/3.2.1/gallery/ - 3D rendering
https://en.wikipedia.org/wiki/3D_rendering - 3D computer graphics
https://en.wikipedia.org/wiki/3D_computer_graphics - Primary 3D view planes
https://matplotlib.org/stable/gallery/mplot3d/view_planes_3d.html - Getting started in scikit-learn with the famous iris dataset
https://www.youtube.com/watch?v=hd1W4CyPX58 - Training a machine learning model with scikit-learn
https://www.youtube.com/watch?v=RlQuVL6-qe8 - Iris (plant)
https://en.wikipedia.org/wiki/Iris_(plant) - Kosatec
https://cs.wikipedia.org/wiki/Kosatec - Iris setosa
https://en.wikipedia.org/wiki/Iris_setosa - Iris versicolor
https://en.wikipedia.org/wiki/Iris_versicolor - Iris virginica
https://en.wikipedia.org/wiki/Iris_virginica - Druh
https://cs.wikipedia.org/wiki/Druh - Iris subg. Limniris
https://en.wikipedia.org/wiki/Iris_subg._Limniris - Iris Dataset Classification with Python: A Tutorial
https://www.pycodemates.com/2022/05/iris-dataset-classification-with-python.html - Iris flower data set
https://en.wikipedia.org/wiki/Iris_flower_data_set - List of datasets for machine-learning research
https://en.wikipedia.org/wiki/List_of_datasets_for_machine-learning_research - Analýza hlavních komponent
https://cs.wikipedia.org/wiki/Anal%C3%BDza_hlavn%C3%ADch_komponent - Principal component analysis
https://en.wikipedia.org/wiki/Principal_component_analysis - Scikit-learn Crash Course – Machine Learning Library for Python
https://www.youtube.com/watch?v=0B5eIE_1vpU - calm-notebooks
https://github.com/koaning/calm-notebooks - Should you teach Python or R for data science?
https://www.dataschool.io/python-or-r-for-data-science/ - nbviewer: A simple way to share Jupyter Notebooks
https://nbviewer.org/ - AI vs Machine Learning (Youtube)
https://www.youtube.com/watch?v=4RixMPF4×is - Machine Learning | What Is Machine Learning? | Introduction To Machine Learning | 2024 | Simplilearn (Youtube)
https://www.youtube.com/watch?v=ukzFI9rgwfU - A Gentle Introduction to Machine Learning (Youtube)
https://www.youtube.com/watch?v=Gv9_4yMHFhI - Machine Learning vs Deep Learning
https://www.youtube.com/watch?v=q6kJ71tEYqM - Umělá inteligence (slajdy)
https://slideplayer.cz/slide/12119218/ - Úvod do umělé inteligence
https://slideplayer.cz/slide/2505525/ - Umělá inteligence I / Artificial Intelligence I
https://ktiml.mff.cuni.cz/~bartak/ui/ - Matplotlib vs. seaborn vs. Plotly vs. MATLAB vs. ggplot2 vs. pandas
https://ritza.co/articles/matplotlib-vs-seaborn-vs-plotly-vs-MATLAB-vs-ggplot2-vs-pandas/ - Matplotlib, Seaborn or Plotnine?
https://www.reddit.com/r/datascience/comments/jvrqxt/matplotlib_seaborn_or_plotnine/ - @Rabeez: Rabeez/plotting_comparison.ipynb
https://gist.github.com/Rabeez/ffc0b59d4a41e20fa8d944c44a96adbc - Matplotlib, Seaborn, Plotly and Plotnine Comparison
https://python.plainenglish.io/matplotlib-seaborn-plotly-and-plotnine-comparison-baf2db5a9c40 - Data Visualization 101: How to Choose a Python Plotting Library
https://towardsdatascience.com/data-visualization-101-how-to-choose-a-python-plotting-library-853460a08a8a - Data science in Python: pandas, seaborn, scikit-learn
https://www.youtube.com/watch?v=3ZWuPVWq7p4 - 7.2. Real world datasets
https://scikit-learn.org/stable/datasets/real_world.html#california-housing-dataset - 7.2.7. California Housing dataset
https://scikit-learn.org/stable/datasets/real_world.html#california-housing-dataset - Comprehensive Guide to Classification Models in Scikit-Learn
https://www.geeksforgeeks.org/comprehensive-guide-to-classification-models-in-scikit-learn/ - Tidy Data Visualization: ggplot2 vs seaborn
https://blog.tidy-intelligence.com/posts/ggplot2-vs-seaborn/ - seaborn: statistical data visualization
https://seaborn.pydata.org/ - Linear regression (Wikipedia)
https://en.wikipedia.org/wiki/Linear_regression - Lineární regrese (Wikipedia)
https://cs.wikipedia.org/wiki/Line%C3%A1rn%C3%AD_regrese




































