Obsah
1. Shluková analýza (clustering) a knihovna Scikit-learn
2. Příklad reálných dat, u nichž lze využít shlukovou analýzu
3. Příprava dat pro shlukovou analýzu
4. Vygenerování sady bodů v rovině funkcí sklearn.datasets.make_blobs
5. Malá odbočka: prohození x-ových a y-ových souřadnic
6. Korelační diagram (bodový graf)
7. Vykreslení bodů vygenerovaných funkcí sklearn.datasets.make_blobs
8. Úprava skriptu pro vykreslení většího množství bodů v rovině
9. Obarvení bodů na základě toho, do jakého clusteru patří
10. Algoritmus K-means pro shlukovou analýzu
11. Nalezení centroidů algoritmem K-means
12. Zobrazení centroidů společně se všemi body v rovině
15. Clustering pro větší počet bodů v případě, kdy se oblasti centroidů překrývají
16. Pokus o nalezení clusterů v náhodných datech
17. Limity standardního algoritmu K-means
19. Repositář s demonstračními příklady
1. Shluková analýza (clustering) a knihovna Scikit-learn
V článku Rozpoznávání obrázků knihovnou Scikit-learn: první kroky jsme se ve stručnosti seznámili s tím, jakým způsobem spolu dokážou kooperovat knihovny NumPy, Pandas (či Polars), Matplotlib a Scikit-Learn. Tuto kooperaci jsme si ukázali na příkladu rozpoznávání ručně napsaných číslic, přičemž knihovna Scikit-Learn byla použita jako zdroj dat pro trénink i validaci, ovšem navíc nám poskytla i model, který jsme mohli natrénovat. Knihovna NumPy v tomto případě zajišťovala podporu základních datových struktur (n-rozměrná pole, nd-array) i algoritmů a knihovna Matplotlib sloužila pro vizualizaci vstupních dat, mezivýsledků i výsledků poskytovaných natrénovaným modelem.

Obrázek 1: Prvních patnáct číslic, které jsme v předchozím článku použili pro trénink modelu.
Ovšem knihovna Scikit-learn ve skutečnosti nemusí být použita pouze pro trénink modelů; dokonce je možné říci, že je to pro mnoho uživatelů zcela okrajové téma. Scikit-learn totiž poskytuje i mnoho dalších nástrojů. Jedním z velmi užitečných nástrojů, které zde nalezneme, je podpora pro provádění takzvané shlukové analýzy (cluster analysis, clustering). Jedná se o proces, který se používá jako vstup pro klasifikaci objektů. Zjednodušeně řečeno se používá k rozdělení vstupních dat (či již nějakým způsobem upravených dat) do skupin, přičemž se očekává, že data, která budou náležet do stejné skupiny, budou představovat objekty (i když možná by bylo lepší říci informace) s podobnými vlastnostmi.

Obrázek 2: Výsledky modelu, který jsme natrénovali v rámci předchozího článku.
2. Příklad reálných dat, u nichž lze využít shlukovou analýzu
Poměrně dobrým příkladem toho, kde může být shluková analýza užitečná, mohou být data zjištěná o nějaké hvězdě (například informace o teplotě a zářivém výkonu nebo velikosti). Pokud vyneseme do jednoduchého dvourozměrného grafu hodnoty pro tyto dvě veličiny pro všechny pozorované (a změřené) hvězdy, získáme slavný Hertzsprungův–Russellův diagram, zkráceně též H–R diagram, který vypadá následovně:
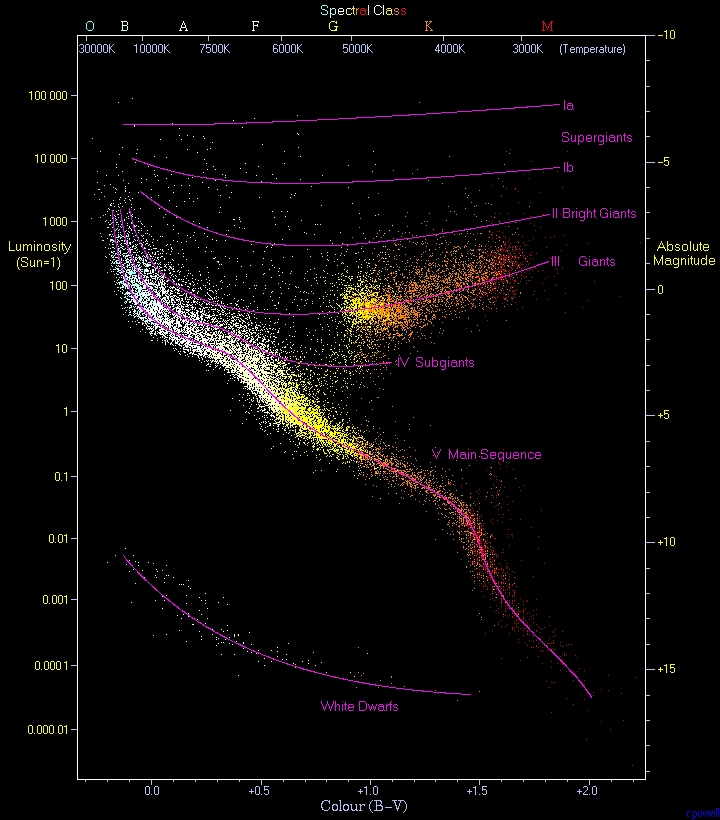
Obrázek 3: Ukázka H–R diagramu.
Autor: Adam na projektu Wikipedie v jazyce čeština – Na Commons přeneseno z cs.wikipedia., Volné dílo, https://commons.wikimedia.org/w/index.php?curid=2157609
Na H-R diagramu jsou jasně patrné oblasti, do nichž jsou sdruženy hvězdy s podobnými vlastnostmi (dokonce můžeme říci, že s podobným osudem). A úkolem shlukové analýzy (clusteringu) je tyto oblasti nalézt, resp. vypočítat. V tomto konkrétním případě je to relativně jednoduchá úloha, ovšem pochopitelně se v praxi ne vždy data shlukují takto „pěkným“ způsobem. Z tohoto důvodu existuje hned několik algoritmů pro shlukovou analýzu – a nejtěžším úkolem je vybrat si ten správný algoritmus a určit jeho parametry.
3. Příprava dat pro shlukovou analýzu
Dnes si otestujeme jeden konkrétní algoritmus určený pro provedení shlukové analýzy, který se nazývá K-means clustering. Ovšem nejprve si musíme připravit vhodná data, na kterých bude možné si vizuálně ověřit výsledky tohoto algoritmu. Jak již víme z předchozího textu, může být shluková analýza provedena v prakticky libovolném počtu dimenzí, ovšem pro jednoduchost začneme dvoudimenzionálními daty. V praxi se tedy bude jednat o sadu hodnot dvou veličin (nebo jedné veličiny) – například již zmíněné teploty a zářivém výkonu hvězdy. Pro každý objekt vyneseme jednu hodnotu na x-ovou osu a druhou hodnotu na y-ovou osu. Výsledkem bude bod v rovině.
Pro naše pokusy tedy potřebujeme získat sadu bodů v rovině, které však nebudou rozmístěny zcela náhodně (tam poněkud postrádá shluková analýza smysl). Existuje mnoho způsobů, jak body v rovině rozmístit. Pro velkou názornost jsem pro dnešní článek vybral metodu realizovanou ve funkci sklearn.datasets.make_blobs, která nejprve vybere n centrálních bodů a poté rozmisťuje další body okolo těchto center tak, že pravděpodobnost umístění bodu dále od centra klesá podle Gaussovy křivky (teoreticky tedy může být bod umístěn na ploše kdekoli, ovšem s větší vzdáleností od centrálních bodů pravděpodobnost jeho umístění do daného místa klesá – což si ověříme vizuálně).
4. Vygenerování sady bodů v rovině funkcí sklearn.datasets.make_blobs
Podívejme se nyní na praktické použití funkce sklearn.datasets.make_blobs. Této funkci musíme předat především počet bodů, které se mají vygenerovat (n_samples), počet centrálních bodů (centers) a další parametry ovlivňující generování bodů (směrodatná odchylka atd.). Výsledkem bude dvojice hodnot – pole se samotnými body a taktéž pole obsahující pro každý vygenerovaný bod index centrálního body (centroidu), který je k němu nejblíže (resp. přesněji index centrálního bodu, který byl použit v algoritmu výpočtu pseudonáhodné pozice):
# import funkce, která dokáže vygenerovat množinu bodů v rovině sdružených do oblastí
from sklearn.datasets import make_blobs
# testovací data
n_samples = 20
# počet oblastí, kam se budou data sdružovat
n_components = 6
# vygenerovat množinu bodů v rovině sdružených do oblastí
samples, labels = make_blobs(
n_samples=n_samples, centers=n_components, cluster_std=0.60, random_state=0
)
print("Points:")
print(samples)
print()
print("Labels:")
print(labels)
Výsledky mohou pro daný počet dvaceti bodů vypadat následovně:
Before swap: [[-1.45700306 7.9292694 ] [ 3.4171203 0.02504426] [-1.48065187 7.65407837] [-0.60723648 3.79949752] [ 5.29722082 0.81003989] [ 8.9674639 -2.5940142 ] [ 2.08272263 0.78535335] [-2.05957546 1.72940438] [ 4.86616205 0.45025423] [ 8.2494931 -1.16070439] [-0.51008137 8.55688792] [ 0.52347363 1.28983482] [ 1.87271752 4.18069237] [ 1.24258802 4.50399192] [ 5.08282355 1.04439261] [ 8.64412343 -3.18318039] [ 2.57392924 0.45236465] [ 1.43289271 4.37679234] [ 1.1641107 3.79132988] [-1.43393556 3.14477977]] Labels: [3 1 3 2 5 4 1 2 5 4 3 1 0 0 5 4 1 0 0 2]
5. Malá odbočka: prohození x-ových a y-ových souřadnic
Při vizualizaci bodů v rovině je mnohdy vhodné prohodit jejich x-ové a y-ové souřadnice (což může být případ výše zmíněného HR-diagramu). V praxi toho dosáhneme velmi snadno, protože knihovna NumPy u n-rozměrných polí přetěžuje jak operátor indexování, tak i operátor pro provedení řezu (slice). V případě dvourozměrného pole, kde souřadnice jsou uloženy ve dvou sloupcích, lze prohození sloupců s x-ovými a y-ovými souřadnicemi realizovat následovně:
samples = samples[:, ::-1]
Což si lze snadno otestovat:
# import funkce, která dokáže vygenerovat množinu bodů v rovině sdružených do oblastí
from sklearn.datasets import make_blobs
# testovací data
n_samples = 20
# počet oblastí, kam se budou data sdružovat
n_components = 6
# vygenerovat množinu bodů v rovině sdružených do oblastí
samples, labels = make_blobs(
n_samples=n_samples, centers=n_components, cluster_std=0.60, random_state=0
)
print("Before swap:")
print(samples)
print()
samples = samples[:, ::-1]
print("After swap:")
print(samples)
print()
print("Labels:")
print(labels)
Po spuštění tohoto skriptu se opět vypíšou souřadnice dvaceti bodů. Tentokrát však budou odlišné od příkladu z předchozí kapitoly, protože došlo k prohození x-ových a y-ových souřadnic:
Before swap: [[-1.45700306 7.9292694 ] [ 3.4171203 0.02504426] [-1.48065187 7.65407837] [-0.60723648 3.79949752] [ 5.29722082 0.81003989] [ 8.9674639 -2.5940142 ] [ 2.08272263 0.78535335] [-2.05957546 1.72940438] [ 4.86616205 0.45025423] [ 8.2494931 -1.16070439] [-0.51008137 8.55688792] [ 0.52347363 1.28983482] [ 1.87271752 4.18069237] [ 1.24258802 4.50399192] [ 5.08282355 1.04439261] [ 8.64412343 -3.18318039] [ 2.57392924 0.45236465] [ 1.43289271 4.37679234] [ 1.1641107 3.79132988] [-1.43393556 3.14477977]] After swap: [[ 7.9292694 -1.45700306] [ 0.02504426 3.4171203 ] [ 7.65407837 -1.48065187] [ 3.79949752 -0.60723648] [ 0.81003989 5.29722082] [-2.5940142 8.9674639 ] [ 0.78535335 2.08272263] [ 1.72940438 -2.05957546] [ 0.45025423 4.86616205] [-1.16070439 8.2494931 ] [ 8.55688792 -0.51008137] [ 1.28983482 0.52347363] [ 4.18069237 1.87271752] [ 4.50399192 1.24258802] [ 1.04439261 5.08282355] [-3.18318039 8.64412343] [ 0.45236465 2.57392924] [ 4.37679234 1.43289271] [ 3.79132988 1.1641107 ] [ 3.14477977 -1.43393556]] Labels: [3 1 3 2 5 4 1 2 5 4 3 1 0 0 5 4 1 0 0 2]
6. Korelační diagram (bodový graf)
Body vytvořené předchozími dvěma skripty je možné vykreslit (vizualizovat) několika způsoby, ovšem jediným typem grafu, se kterým se dnes seznámíme, je takzvaný korelační diagram, který je ovšem někdy známý i pod jménem bodový graf (scatter plot). Tento graf se v knihovně Matplotlib vykresluje funkcí matplotlib.pyplot.scatter, které se předají minimálně informace o x-ových a y-ových souřadnicích bodů, jež se mají do grafu vykreslit.
Všechny x-ové a všechny y-ové souřadnice získáme z našeho 2D pole (matice) takto:
xs = samples[:, 0] ys = samples[:, 1]
7. Vykreslení bodů vygenerovaných funkcí sklearn.datasets.make_blobs
Ukažme si tedy, jakým způsobem je možné v praxi realizovat vykreslení bodů se souřadnicemi vygenerovanými funkcí sklearn.datasets.make_blobs. K tomuto účelu použijeme funkci nazvanou matplotlib.pyplot.scatter, které se v tom nejjednodušším případě předají dva vektory (jednorozměrná pole). V prvním vektoru budou uloženy x-ové souřadnice bodů, ve druhém vektoru pak jejich y-ové souřadnice. Souřadnice grafu budou upraveny takovým způsobem, aby se zobrazily všechny body a navíc aby byla plocha grafu vyplněna (bez prázdných oblastí):
# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
# import funkce, která dokáže vygenerovat množinu bodů v rovině sdružených do oblastí
from sklearn.datasets import make_blobs
# testovací data
n_samples = 100
# počet oblastí, kam se budou data sdružovat
n_components = 6
# vygenerovat množinu bodů v rovině sdružených do oblastí
samples, labels = make_blobs(
n_samples=n_samples, centers=n_components, cluster_std=0.60, random_state=0
)
samples = samples[:, ::-1]
# vykreslení bodů v rovině
plt.scatter(samples[:, 0], samples[:, 1])
# uložení grafu do souboru
plt.savefig("scatter_1.png")
# vykreslení na obrazovku
plt.show()
Výsledek bude vypadat následovně:
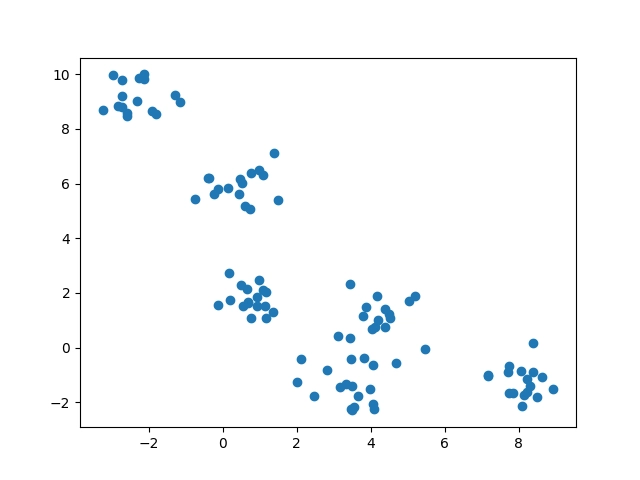
Obrázek 4: Zobrazení 100 bodů rozmístěných v rovině pseudonáhodným způsobem.
8. Úprava skriptu pro vykreslení většího množství bodů v rovině
Výše uvedený příklad je vhodné použít ve chvíli, kdy se má zobrazit relativně malé množství bodů, odhadem několik set. Pokud je však bodů větší množství, budou se překrývat, protože jejich stopy v grafu jsou příliš velké. Ovšem je relativně snadné změnit jak tvar zobrazené stopy (parametr marker), tak i její velikost (parametr size). U velikosti je však vhodné si uvědomit, že je udávána nikoli v pixelech, ale v typografických bodech (1/72 palce), podobně jako na mnoha dalších místech Matplotlibu. Velikost je tedy poměrně špatné odhadnout a je tedy vhodné skript spustit s několika parametry a vybrat si tu „správnou“ velikost (záleží i na tom, jak se body shlukují apod.).
V dalším příkladu se pokusíme o zobrazení 1000 bodů, jejichž stopy však budou menší, než tomu bylo v předchozím demonstračním příkladu:
# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
# import funkce, která dokáže vygenerovat množinu bodů v rovině sdružených do oblastí
from sklearn.datasets import make_blobs
# testovací data
n_samples = 1000
# počet oblastí, kam se budou data sdružovat
n_components = 6
# vygenerovat množinu bodů v rovině sdružených do oblastí
samples, labels = make_blobs(
n_samples=n_samples, centers=n_components, cluster_std=0.60, random_state=0
)
samples = samples[:, ::-1]
# vykreslení bodů v rovině
plt.scatter(samples[:, 0], samples[:, 1], marker=".", s=10)
# uložení grafu do souboru
plt.savefig("scatter_2.png")
# vykreslení na obrazovku
plt.show()
A takto by měl vypadat výsledek:
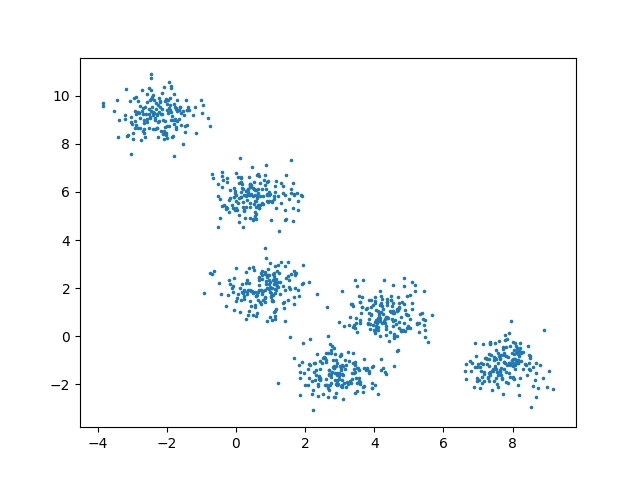
Obrázek 5: Zobrazení 1000 bodů rozmístěných v rovině pseudonáhodným způsobem.
9. Obarvení bodů na základě toho, do jakého clusteru patří
V předchozím textu jsme si řekli, že funkce sklearn.datasets.make_blobs vrací nejenom souřadnice bodů, ale i index (celé číslo) udávající oblast (řekněme poněkud nepřesně cluster), do které daný bod náleží. Tuto hodnotu můžeme využít ke dvěma účelům:
- Pro ověření algoritmu pro shlukovou analýzu
- Pro vizualizaci bodů, přesněji řečeno pro jejich obarvení podle oblasti
Vyzkoušejme si nyní obarvení bodů podle oblasti. Je to snadné. Vytvoříme si seznam (či n-tici) se šesti kódy barev:
colors = ["#4444cc", "#44bb44", "#cc4444", "#cccc44", "#44cccc", "#cc44cc"]
Dále budeme iterovat přes prvky této kolekce a vykreslíme pouze ty body, které mají shodnou hodnotu label s indexem barvy (0–5):
for i, color in enumerate(colors):
...
...
...
Jak se vlastně provádí výběr bodů z dvourozměrného pole? Nejprve si vytvoříme pomocný vektor obsahující pouze 0 a 1, kde 1 znamená, že se má příslušný bod vybrat. Tento vektor bude použit jako selektor do původního dvourozměrného pole se souřadnicemi:
for i, color in enumerate(colors):
selector = labels == i
Zbývá nám jen selektor použít a vykreslit body zadanou barvou:
for i, color in enumerate(colors):
selector = labels == i
plt.scatter(samples[selector, 0], samples[selector, 1], c=color, marker=".", s=10)
Výsledek by měl vypadat následovně:
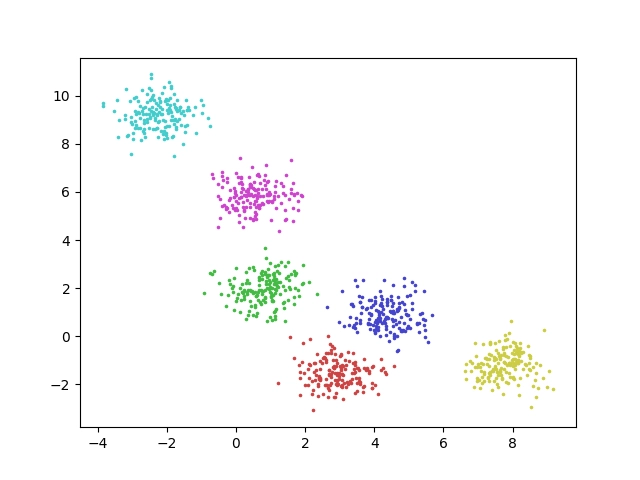
Obrázek 6: Obarvení bodů na základě toho, do jakého clusteru patří.
Pro jistotu si ukažme celý skript, který toto vykreslení provede:
# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
# import funkce, která dokáže vygenerovat množinu bodů v rovině sdružených do oblastí
from sklearn.datasets import make_blobs
# testovací data
n_samples = 1000
# počet oblastí, kam se budou data sdružovat
n_components = 6
# vygenerovat množinu bodů v rovině sdružených do oblastí
samples, labels = make_blobs(
n_samples=n_samples, centers=n_components, cluster_std=0.60, random_state=0
)
samples = samples[:, ::-1]
# vykreslení bodů v rovině s jejich obarvením na základě labelu
plt.figure(1)
colors = ["#4444cc", "#44bb44", "#cc4444", "#cccc44", "#44cccc", "#cc44cc"]
for i, color in enumerate(colors):
selector = labels == i
plt.scatter(samples[selector, 0], samples[selector, 1], c=color, marker=".", s=10)
# uložení grafu do souboru
plt.savefig("scatter_3.png")
# vykreslení na obrazovku
plt.show()
10. Algoritmus K-means pro shlukovou analýzu
Vzhledem k tomu, že cíle shlukové analýzy jsou poměrně rozmanité a různé je i rozmístění bodů, pro které hledáme vhodné clustery, existuje minimálně několik desítek algoritmů, které shlukovou analýzu provádí. Tyto algoritmy se liší jak svou výpočetní složitostí, tak i způsobem vyhledání clusterů. Pro potřeby dnešního článku byl vybrán pravděpodobně nejznámější algoritmus shlukové analýzy, který se jmenuje K-means. Tento algoritmus je založen na předpokladu, že vstupní objekty jsou chápány jako skutečné body v nějakém eukleidovském prostoru a již dopředu víme, kolik shluků (clusterů) má existovat. Algoritmus nejprve nalezne takzvané centroidy a následně jsou vstupní objekty (body) zařazeny k tomu centroidu, který je k bodu nejblíže. Poté se provádí další iterace; centroidy se přesunou do těžiště clusteru a provede se nové přiřazení.
11. Nalezení centroidů algoritmem K-means
Prvním úkolem algoritmu K-means je nalezení centroidů, tedy centra oblastí, v nichž se body shlukují. V knihovně Scikit-learn můžeme tuto operaci provést s využitím funkce kmeans_plusplus (viz též tento článek). Tato funkce vrací ve své první návratové hodnotě dvourozměrné pole s nalezenými centry oblastí. Povšimněte si, že funkci kmeans_plusplus předáváme nejenom samotné pole se souřadnicemi bodů, ale i předpokládaný počet oblastí. Tuto hodnotu tedy musíme dopředu znát či ji odhadnout (a postupovat iterativním způsobem):
# nalézt centra oblastí centers_init, indices = kmeans_plusplus(samples, n_clusters=6, random_state=0)
Získané dvourozměrné pole s centroidy lze vykreslit způsobem, který již dobře známe. Centroidů je nepatrný počet (6), takže je vykreslíme s využitím větších stop (s=50) a pro přehlednost použijeme červenou barvu:
plt.scatter(centers_init[:, 0], centers_init[:, 1], c="red", s=50)
Výsledek by měl vypadat následovně:
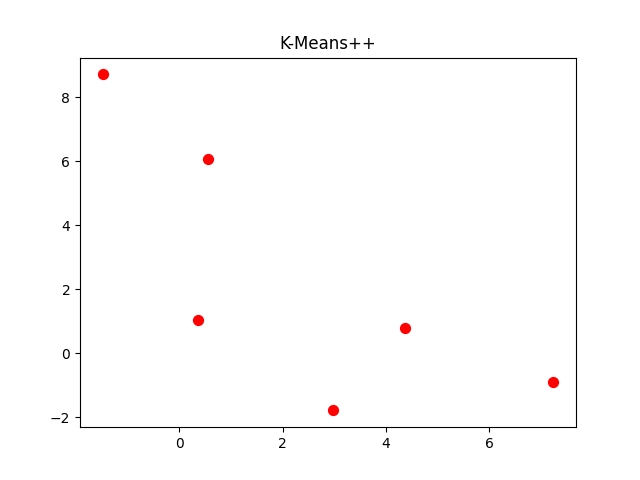
Obrázek 7: Vizualizace centroidů nalezených algoritmem K-means.
Opět si pro jistotu ukažme celý skript, který tuto operaci provádí:
# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
# funkce s implementací algoritmu pro clustering
from sklearn.cluster import kmeans_plusplus
# import funkce, která dokáže vygenerovat množinu bodů v rovině sdružených do oblastí
from sklearn.datasets import make_blobs
# testovací data
n_samples = 1000
# počet oblastí, kam se budou data sdružovat
n_components = 6
# vygenerovat množinu bodů v rovině sdružených do oblastí
samples, labels = make_blobs(
n_samples=n_samples, centers=n_components, cluster_std=0.60, random_state=0
)
samples = samples[:, ::-1]
# nalézt centra oblastí
centers_init, indices = kmeans_plusplus(samples, n_clusters=6, random_state=0)
plt.scatter(centers_init[:, 0], centers_init[:, 1], c="red", s=50)
plt.title("K-Means++")
# uložení grafu do souboru
plt.savefig("k_means_1.png")
# vykreslení na obrazovku
plt.show()
12. Zobrazení centroidů společně se všemi body v rovině
Pro ověření, zda vypočtené centroidy skutečně leží (blízko) středů jednotlivých clusterů, je pochopitelně nejlepší si nechat na jednom grafu zobrazit jak vstupní body (vygenerované funkcí make_blobs), tak i vlastní centroidy. Tuto funkcionalitu knihovna Matplotlib podporuje, protože na jednu plochu výsledného grafu můžeme vložit větší množství korelačních diagramů (což jsme si již ostatně ukázali při „obarvování“ bodů). Skript pro výpočet centroidů a vizualizaci výsledků tedy můžeme upravit do následující podoby:
# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
# funkce s implementací algoritmu pro clustering
from sklearn.cluster import kmeans_plusplus
# import funkce, která dokáže vygenerovat množinu bodů v rovině sdružených do oblastí
from sklearn.datasets import make_blobs
# testovací data
n_samples = 1000
# počet oblastí, kam se budou data sdružovat
n_components = 6
# vygenerovat množinu bodů v rovině sdružených do oblastí
samples, labels = make_blobs(
n_samples=n_samples, centers=n_components, cluster_std=0.60, random_state=0
)
samples = samples[:, ::-1]
# vykreslení bodů v rovině s jejich obarvením na základě labelu
plt.figure(1)
colors = ["#4444cc", "#44bb44", "#cc4444", "#cccc44", "#44cccc", "#cc44cc"]
for i, color in enumerate(colors):
selector = labels == i
plt.scatter(samples[selector, 0], samples[selector, 1], c=color, marker=".", s=10)
# nalézt centra oblastí
centers_init, indices = kmeans_plusplus(samples, n_clusters=6, random_state=0)
plt.scatter(centers_init[:, 0], centers_init[:, 1], c="red", s=50)
plt.title("K-Means++")
# uložení grafu do souboru
plt.savefig("k_means_2.png")
# vykreslení na obrazovku
plt.show()
A takto by měl vypadat výsledek:
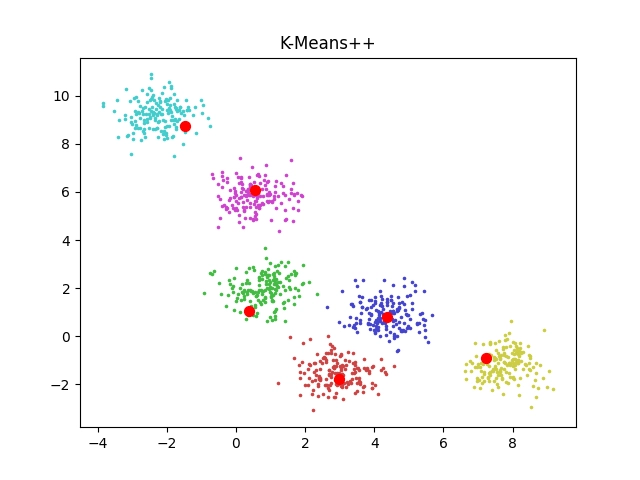
Obrázek 8: Vizualizace centroidů nalezených algoritmem K-means zkombinovaná s původními vstupními body.
13. Výpočet clusterů
Pro výpočet clusterů, tedy pro rozřazení bodů do jednotlivých clusterů, se nepoužívá funkce kmeans_plusplus, protože ta „pouze“ nalezne centroidy. Musíme namísto ní použít nepatrně složitější způsob. Nejprve zkonstruujeme instanci třídy KMeans, které je opět nutné předat očekávaný počet clusterů. Následně výslednému objektu předáme vstupní body a zahájíme výpočet pro nalezení clusterů metodou fit:
# clustering kmeans = KMeans(n_clusters=6, random_state=0, n_init="auto").fit(samples)
Objekt, který získáme po dokončení metody fit, obsahuje mj. i dvojici atributů nazvaných labels_ a centers_. V prvním z těchto atributů jsou uloženy indexy clusterů (číslují se od jedničky) pro všechny vstupní body (tedy například index 3 na pozici n znamená, že bod n patří ke clusteru číslo 3). A druhý atribut centers_ obsahuje souřadnice centroidů.
Oba atributy si necháme vypočítat a vypsat následujícím skriptem:
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
# testovací data
n_samples = 1000
# počet oblastí, kam se budou data sdružovat
n_components = 6
samples, labels = make_blobs(
n_samples=n_samples, centers=n_components, cluster_std=0.60, random_state=0
)
samples = samples[:, ::-1]
# clustering
kmeans = KMeans(n_clusters=6, random_state=0, n_init="auto").fit(samples)
print("Labels:")
print(kmeans.labels_)
print()
print("Centroids:")
print(kmeans.cluster_centers_)
Výsledky získané po spuštění skriptu:
Labels: [4 1 0 5 4 2 4 0 1 2 3 3 4 0 3 0 1 3 3 4 3 3 0 3 3 4 1 2 1 2 0 2 2 5 3 4 1 4 3 4 3 1 2 1 4 0 1 2 5 5 2 0 1 2 2 2 5 0 1 3 3 4 0 4 3 5 2 3 5 5 1 3 2 4 4 4 1 3 3 4 4 4 3 5 0 5 4 0 4 4 5 3 1 1 0 2 5 4 3 3 1 5 0 5 3 0 3 5 0 1 2 1 2 0 2 2 2 3 2 5 3 3 3 5 3 4 2 4 1 2 2 1 5 3 0 4 1 5 0 3 1 1 5 2 2 3 0 3 3 5 3 4 4 4 2 0 5 3 4 2 0 3 2 4 5 3 0 3 4 0 3 4 3 1 4 0 4 3 1 3 3 3 5 2 4 3 5 2 0 2 2 5 0 4 1 0 5 1 3 5 3 2 3 2 2 5 2 1 0 0 0 4 1 0 2 4 4 1 5 0 0 4 2 3 0 3 1 1 2 0 5 1 5 2 3 1 0 4 2 3 0 4 0 0 1 2 1 0 3 0 0 2 0 3 2 4 1 4 5 3 4 5 1 3 5 4 1 3 2 3 0 1 3 5 1 0 4 3 1 4 4 4 0 5 4 4 4 1 4 1 0 5 2 0 0 1 4 4 3 1 4 1 5 0 4 2 2 0 0 0 4 0 2 4 5 2 1 0 3 5 3 3 3 4 0 4 3 1 2 3 4 3 2 0 2 4 3 4 5 1 4 2 0 2 4 2 1 2 3 5 3 1 3 5 0 2 5 5 1 4 0 4 0 1 0 3 4 2 2 2 0 3 3 0 5 4 2 1 4 1 3 4 0 2 5 4 5 1 0 4 4 4 3 5 5 2 0 5 4 1 2 4 2 4 5 4 2 5 1 5 0 3 5 4 3 4 2 1 4 3 3 3 2 1 3 2 2 1 0 3 4 0 5 3 4 4 2 4 0 1 2 0 0 2 2 4 5 4 0 1 3 5 4 5 4 1 2 2 0 5 3 3 3 1 5 3 4 1 5 2 0 4 0 0 2 5 0 2 4 5 5 1 4 5 3 1 3 0 0 3 3 0 1 2 0 4 3 0 0 4 2 2 4 1 4 2 5 2 2 4 2 0 2 0 5 3 1 5 1 0 4 4 5 5 1 2 4 0 1 3 3 1 5 0 5 3 2 2 2 1 2 2 1 2 3 4 5 5 0 0 3 5 3 1 2 1 0 2 3 4 4 4 0 1 2 0 0 0 4 2 2 0 0 5 2 2 2 4 4 0 2 4 2 5 5 0 5 0 3 5 1 4 2 0 3 3 1 2 3 1 0 1 3 1 2 1 1 4 4 5 5 3 2 0 1 1 0 5 3 1 1 3 5 2 2 3 0 0 2 4 4 5 1 4 4 5 3 1 4 4 4 4 3 3 5 5 5 2 2 5 3 0 3 3 3 4 1 1 0 2 0 4 1 3 2 4 3 1 1 4 3 5 2 2 3 2 2 4 3 1 2 5 0 5 4 5 1 3 5 4 0 0 0 2 2 0 1 1 4 0 1 4 5 5 0 0 5 1 2 3 0 1 5 1 3 5 1 5 4 0 0 0 0 5 2 4 0 2 3 1 5 5 1 5 1 5 3 4 0 5 2 3 3 1 0 3 0 5 2 0 3 4 2 5 1 1 5 1 5 0 3 2 5 2 0 2 5 5 0 5 3 1 1 5 5 1 4 3 5 5 5 1 3 5 0 5 0 4 4 5 5 3 1 1 3 5 4 1 0 5 1 0 4 1 3 4 3 1 1 4 5 5 2 5 1 1 3 0 4 3 0 0 2 0 2 1 0 2 1 0 1 0 1 2 1 5 0 2 0 0 0 5 1 5 2 2 3 2 5 5 4 5 2 2 2 1 2 4 2 1 4 5 0 5 4 0 1 0 1 3 1 5 1 0 1 0 3 4 1 5 4 5 2 5 1 1 5 5 0 3 5 2 1 3 0 2 1 5 3 4 5 1 4 4 0 0 3 0 2 4 3 3 5 2 3 5 1 1 3 1 0 5 1 5 3 0 1 2 3 1 5 3 5 0 3 0 0 5 3 1 5 4 0 2 1 2 5 5 5 2 3 3 4 4 4 2 2 5 3 4 1 5 0 4 1 4 2 3 2 1 1 4 4 3 1 2 3 4 2 2 2 5 2 5 0 2 5 2 5 1 5 4 1 1 4 1 1 5 1 0] Centroids: [[ 0.81049056 1.983196 ] [-2.23667661 9.21962615] [ 7.77287664 -1.16476714] [ 4.33349676 0.90584235] [ 0.53153869 5.83908411] [ 2.92830112 -1.52190078]]
14. Vizualizace clusterů
Nyní již máme k dispozici všechny potřebné typy informací:
- Souřadnice vstupních bodů
- Souřadnice centroidů šesti clusterů (viz předchozí kapitolu)
- Určení, do kterého clusteru patří každý vstupní body (taktéž viz předchozí kapitolu)
Tyto tři typy informací nyní zkombinujeme a necháme si je zobrazit na jediném grafu. Jak se zobrazují souřadnice bodů i souřadnice centroidů již známe. Dokonce již víme, jak můžeme body obarvit. Ovšem tentokrát je budeme obarvovat na základě toho, do kterého clusteru byly body přiřazeny algoritmem K-means (budeme tedy ignorovat vektor labels). Pojďme na to:
# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
# třída s implementací algoritmu pro clustering
from sklearn.cluster import KMeans
# import funkce, která dokáže vygenerovat množinu bodů v rovině sdružených do oblastí
from sklearn.datasets import make_blobs
# testovací data
n_samples = 1000
# počet oblastí, kam se budou data sdružovat
n_components = 6
# vygenerovat množinu bodů v rovině sdružených do oblastí
samples, labels = make_blobs(
n_samples=n_samples, centers=n_components, cluster_std=0.60, random_state=0
)
samples = samples[:, ::-1]
plt.figure(1)
colors = ["#4444cc", "#44bb44", "#cc4444", "#cccc44", "#44cccc", "#cc44cc"]
# clustering
kmeans = KMeans(n_clusters=6, random_state=0, n_init="auto").fit(samples)
#print(kmeans.labels_)
#print(kmeans.cluster_centers_)
# vykreslení bodů s jejich přiřazením ke clusteru
for i, color in enumerate(colors):
selector = kmeans.labels_ == i
plt.scatter(samples[selector, 0], samples[selector, 1], c=color, marker=".", s=1)
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], c="red", s=50)
plt.title("K-Means++")
# uložení grafu do souboru
plt.savefig("k_means_3.png")
# vykreslení na obrazovku
plt.show()
Výsledek vypadá korektně:
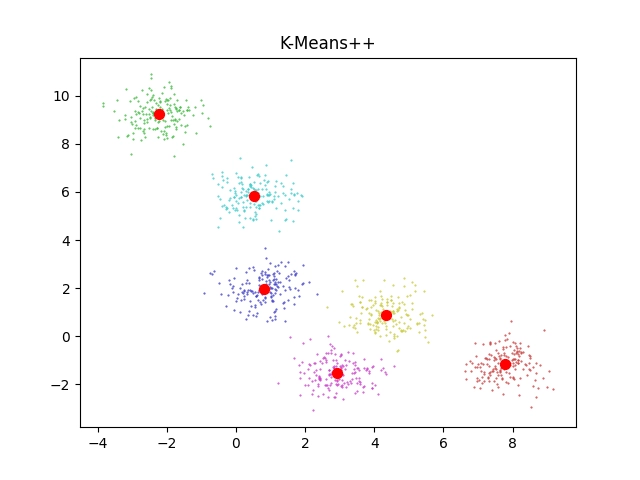
Obrázek 9: Vstupní body, centroidy i rozdělení bodů do jednotlivých clusterů; vše na jediném grafu.
15. Clustering pro větší počet bodů v případě, kdy se oblasti centroidů překrývají
Změnou hodnoty směrodatné odchylky (viz zvýrazněný parametr funkce make_blobs) lze dosáhnout různé hustoty bodů, které budou posléze rozdělovány do clusterů (body mohou být více seskupeny okolo centra či naopak mohou být rozmístěny do větší plochy prostoru). Pokusme se tedy směrodatnou odchylku zvětšit, což by mělo vést k tomu, že se body rozmístí dále od center a navíc se budou jednotlivé oblasti centroidů více překrývat. Tím lépe pochopíme činnosti algoritmu K-means:
# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
# třída s implementací algoritmu pro clustering
from sklearn.cluster import KMeans
# import funkce, která dokáže vygenerovat množinu bodů v rovině sdružených do oblastí
from sklearn.datasets import make_blobs
# testovací data
n_samples = 10000
# počet oblastí, kam se budou data sdružovat
n_components = 6
# vygenerovat množinu bodů v rovině sdružených do oblastí
samples, labels = make_blobs(
n_samples=n_samples, centers=n_components, cluster_std=2.00, random_state=0
)
samples = samples[:, ::-1]
plt.figure(1)
colors = ["#4444cc", "#44bb44", "#cc4444", "#cccc44", "#44cccc", "#cc44cc"]
# clustering
kmeans = KMeans(n_clusters=6, random_state=0, n_init="auto").fit(samples)
#print(kmeans.labels_)
#print(kmeans.cluster_centers_)
# vykreslení bodů s jejich přiřazením ke clusteru
for i, color in enumerate(colors):
selector = kmeans.labels_ == i
plt.scatter(samples[selector, 0], samples[selector, 1], c=color, marker=".", s=1)
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], c="red", s=50)
plt.title("K-Means++")
# uložení grafu do souboru
plt.savefig("k_means_4.png")
# vykreslení na obrazovku
plt.show()
Na výsledném grafu jsou patrné hranice mezi clustery a výsledek (nikoli náhodou!) připomíná Voronoiův diagram:
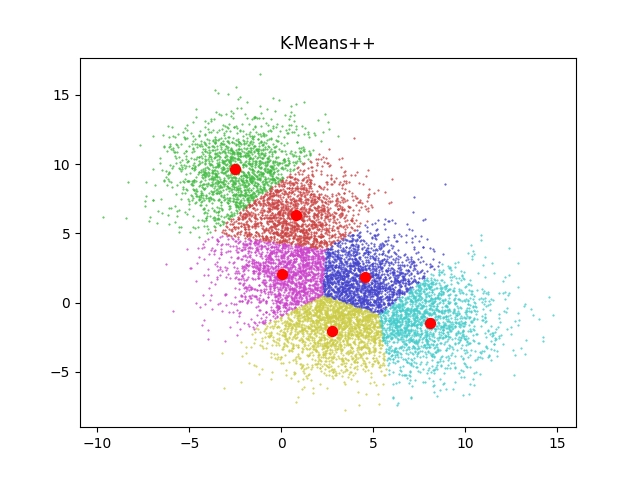
Obrázek 10: Výsledek clusteringu pro překrývající se oblasti centroidů.
16. Pokus o nalezení clusterů v náhodných datech
Pro zajímavost se podívejme na to, jak bude shluková analýza provedená algoritmem K-means provedena na náhodných datech získaných funkcí numpy.random.rand namísto funkce sklearn.datasets.make_blobs. Upravíme tedy pouze jediný řádek ve skriptu a budeme vyžadovat rozdělení bodů do šesti clusterů:
# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
import numpy as np
# testovací data
n_samples = 10000
# počet oblastí, kam se budou data sdružovat
n_components = 6
samples = np.random.rand(n_samples, 2)
samples = samples[:, ::-1]
plt.figure(1)
colors = ["#4444cc", "#44bb44", "#cc4444", "#cccc44", "#44cccc", "#cc44cc"]
# clustering
kmeans = KMeans(n_clusters=6, random_state=0, n_init="auto").fit(samples)
#print(kmeans.labels_)
#print(kmeans.cluster_centers_)
# vykreslení bodů s jejich přiřazením ke clusteru
for i, color in enumerate(colors):
selector = kmeans.labels_ == i
plt.scatter(samples[selector, 0], samples[selector, 1], c=color, marker=".", s=1)
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], c="red", s=50)
plt.title("K-Means++")
# uložení grafu do souboru
plt.savefig(f"k_means_5.png")
# vykreslení na obrazovku
plt.show()
A takto bude vypadat výsledek:
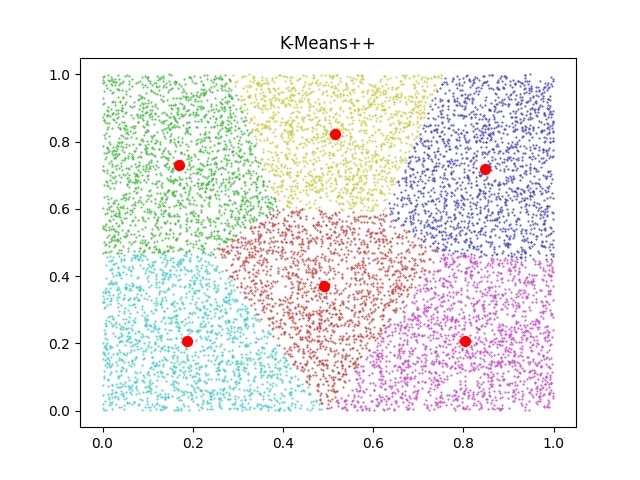
Obrázek 11: Výsledek shlukové analýzy náhodných dat.
17. Limity standardního algoritmu K-means
Algoritmus K-means byl sice v dnešních demonstračních příkladech (až na příklad poslední) úspěšný, což ovšem neznamená, že je tento algoritmus použitelný pro všechny myslitelné účely. Například můžeme předpokládat (a příště si to ověříme), že nedokáže rozdělit hvězdy ve výše zmíněném HR diagramu do logických skupin, tedy do hvězd patřících do hlavní posloupnosti atd. K těmto účelům byly navrženy odlišné algoritmy shlukové analýzy a jedním z předpokladů úspěšné datové analýzy je tyto algoritmy znát (jménem a použitím, ne interní implementaci) a vybrat si ten správný.
18. Obsah navazujícího článku
V navazujícím článku si nejprve ukážeme některé meze algoritmu K-means a posléze se budeme zabývat dalšími vybranými algoritmy, které dokážou provádět shlukové analýzy. Pro otestování chování těchto algoritmů použijeme další funkce pro vygenerování bodů v pseudonáhodných pozicích, tedy funkce obdobné dnes využité funkci make_blobs.
19. Repositář s demonstračními příklady
Všechny demonstrační příklady využívající knihovnu Scikit-learn, které jsme si popsali minule i dnes, lze nalézt v repositáři https://github.com/tisnik/most-popular-python-libs. Následují odkazy na jednotlivé příklady i na (Jupyter) diáře s postupem výpočtů a analýz:
20. Odkazy na Internetu
- scikit-learn: Machine Learning in Python
https://scikit-learn.org/stable/index.html - Sklearn-pandas
https://github.com/scikit-learn-contrib/sklearn-pandas - sklearn-xarray
https://github.com/phausamann/sklearn-xarray/ - Clustering
https://scikit-learn.org/stable/modules/clustering.html - Cluster analysis (Wikipedia)
https://en.wikipedia.org/wiki/Cluster_analysis - Shluková analýza (Wikipedia)
https://cs.wikipedia.org/wiki/Shlukov%C3%A1_anal%C3%BDza - K-means
https://cs.wikipedia.org/wiki/K-means - k-means clustering
https://en.wikipedia.org/wiki/K-means_clustering - Hertzsprungův–Russellův diagram
https://cs.wikipedia.org/wiki/Hertzsprung%C5%AFv%E2%80%93Russell%C5%AFv_diagram - Using Machine Learning in an HR Diagram
https://cocalc.com/share/public_paths/08b6e03583cbdef3cdb9813a54ec68ff773c747f - Gaia H-R diagrams: Querying Gaia data for one million nearby stars
https://vlas.dev/post/gaia-dr2-hrd/ - The Hertzsprung–Russell diagram
https://scipython.com/book2/chapter-9-data-analysis-with-pandas/problems/p92/the-hertzsprung-russell-diagram/ - Animated Hertzsprung-Russell Diagram with 119,614 datapoints
https://github.com/zonination/h-r-diagram - Neuraxle Pipelines
https://github.com/Neuraxio/Neuraxle - scikit-learn: Getting Started
https://scikit-learn.org/stable/getting_started.html - Support Vector Machines
https://scikit-learn.org/stable/modules/svm.html - Use Deep Learning to Detect Programming Languages
http://searene.me/2017/11/26/use-neural-networks-to-detect-programming-languages/ - Natural-language processing
https://en.wikipedia.org/wiki/Natural-language_processing - THE MNIST DATABASE of handwritten digits
http://yann.lecun.com/exdb/mnist/ - MNIST database (Wikipedia)
https://en.wikipedia.org/wiki/MNIST_database - MNIST For ML Beginners
https://www.tensorflow.org/get_started/mnist/beginners - Stránka projektu Torch
http://torch.ch/ - Torch: Serialization
https://github.com/torch/torch7/blob/master/doc/serialization.md - Torch: modul image
https://github.com/torch/image/blob/master/README.md - Data pro neuronové sítě
http://archive.ics.uci.edu/ml/index.php - Torch na GitHubu (několik repositářů)
https://github.com/torch - Torch (machine learning), Wikipedia
https://en.wikipedia.org/wiki/Torch_%28machine_learning%29 - Torch Package Reference Manual
https://github.com/torch/torch7/blob/master/README.md - Torch Cheatsheet
https://github.com/torch/torch7/wiki/Cheatsheet - Neural network containres (Torch)
https://github.com/torch/nn/blob/master/doc/containers.md - Simple layers
https://github.com/torch/nn/blob/master/doc/simple.md#nn.Linear - Transfer Function Layers
https://github.com/torch/nn/blob/master/doc/transfer.md#nn.transfer.dok - Feedforward neural network
https://en.wikipedia.org/wiki/Feedforward_neural_network - Biologické algoritmy (4) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-4-neuronove-site/ - Biologické algoritmy (5) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-5-neuronove-site/ - Umělá neuronová síť (Wikipedia)
https://cs.wikipedia.org/wiki/Um%C4%9Bl%C3%A1_neuronov%C3%A1_s%C3%AD%C5%A5 - PyTorch
http://pytorch.org/ - JupyterLite na PyPi
https://pypi.org/project/jupyterlite/ - JupyterLite na GitHubu
https://github.com/jupyterlite/jupyterlite - Dokumentace k projektu JupyterLite
https://github.com/jupyterlite/jupyterlite - Matplotlib Home Page
http://matplotlib.org/ - Matplotlib (Wikipedia)
https://en.wikipedia.org/wiki/Matplotlib - Popis barvových map modulu matplotlib.cm
https://gist.github.com/endolith/2719900#id7 - Ukázky (palety) barvových map modulu matplotlib.cm
http://matplotlib.org/examples/color/colormaps_reference.html - Galerie grafů vytvořených v Matplotlibu
https://matplotlib.org/3.2.1/gallery/




































