Shluková analýza (clustering) a knihovna Scikit-learn (2)

Obsah

1. Shluková analýza (clustering) a knihovna Scikit-learn (2)

2. Meze algoritmu K-means

3. Pomocná funkce pro vygenerování bodů rozmístěných v soustředných kružnicích

4. Pomocná funkce pro vygenerování bodů rozmístěných do dvou půlměsíců

5. Shluková analýza algoritmem K-means pro body rozmístěné do soustředných kružnic

6. Shluková analýza algoritmem k-means pro body rozmístěné do dvou půlměsíců

7. Shluková analýza realizovaná algoritmem spectral clustering

8. Výsledek shlukové analýzy provedené algoritmem spectral clustering

9. Shluková analýza algoritmem spectral clustering pro body rozmístěné do soustředných kružnic

10. Shluková analýza algoritmem spectral clustering pro body rozmístěné do dvou půlměsíců

11. Meze algoritmu spectral clustering

12. Další algoritmy shlukové analýzy nabízené knihovnou Scikit-Learn

13. Emergence: struktury vzniklé ze zdánlivého chaosu

14. Příklad vzniku emergentní struktury

15. Repositář s demonstračními příklady

16. Odkazy na Internetu

1. Shluková analýza (clustering) a knihovna Scikit-learn (2)

V dnešním článku si nejprve naznačíme některé meze algoritmu K-means, kterým jsme se zabývali v předchozím článku a které omezují použití tohoto algoritmu pouze na některé problémy řešené shlukovou analýzou. Posléze se budeme zabývat dalšími vybranými algoritmy, které dokážou provádět shlukové analýzy a které jsou podporovány knihovnou Scikit-learn. Pro otestování chování těchto algoritmů použijeme další pomocné funkce určené pro vygenerování bodů v pseudonáhodných pozicích, tedy funkce obdobné minule využité funkci make_blobs. V praxi se navíc poměrně často setkáme s požadavkem na nalezení hierarchie shluků (clusterů), což je problém řešitelný algoritmy specializovanými na hierarchickou shlukovou analýzu (ty však mají mnohdy relativně velkou výpočetní složitost).

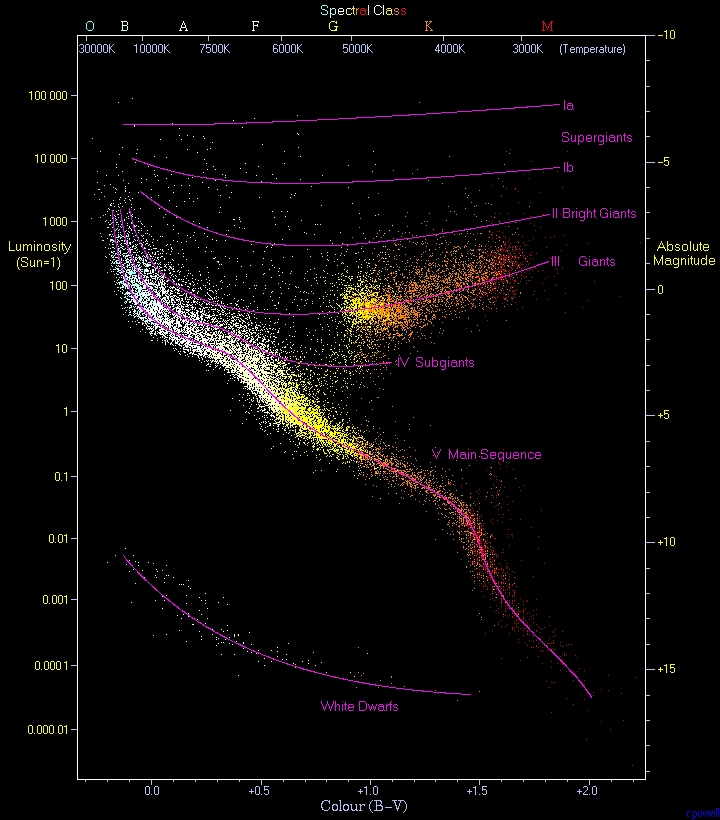
Obrázek 3: Shlukovou analýzu H–R diagramu lze provádět mnohými algoritmy, ovšem algoritmus K-means je pro tyto účely zcela nevhodný.
Autor obrázku: Adam na projektu Wikipedie v jazyce čeština – Na Commons přeneseno z cs.wikipedia., Volné dílo, https://commons.wikimedia­.org/w/index.php?curid=2157609

2. Meze algoritmu K-means

Algoritmus K-means je sice v oblasti shlukové analýzy velmi často využíván, ovšem stále je nutné mít na paměti, že jeho základní vlastnosti do určité míry omezují jeho použití. V případě, že skutečně potřebujeme nalézt skupiny bodů, které se shlukují okolo jednoho bodu (centroidu), lze tento algoritmus použít. Předností bude rychlý výpočet, zejména v porovnání se sofistikovanějšími shlukovými algoritmy. Relativně dobře bude tento algoritmus fungovat i ve chvíli, kdy se oblasti shluků budou překrývat – v takových případech budou hranice mezi shluky připomínat Voronoiův diagram:

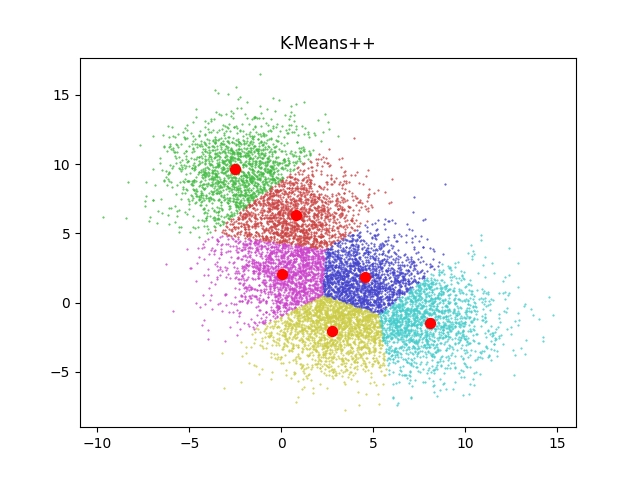
Obrázek 1: Výsledek clusteringu pro překrývající se oblasti centroidů.

V náhodných datech ovšem algoritmus žádnou strukturu nenalezne (což bylo ovšem možné očekávat). Nicméně některé algoritmy tuto situaci dokážou detekovat a vložit všechny body do jediného clusteru:

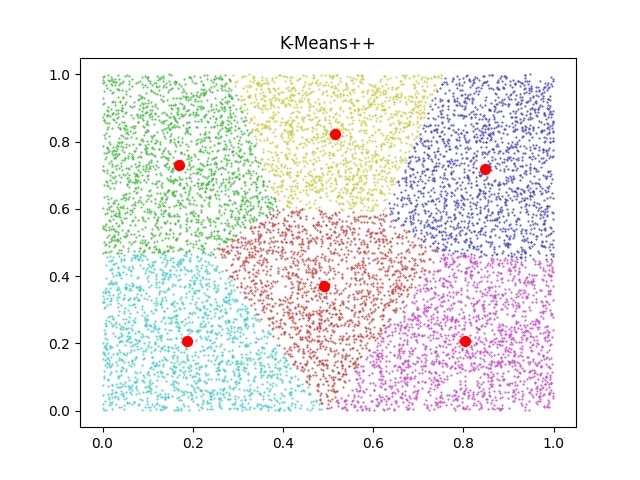
Obrázek 2: Výsledek shlukové analýzy náhodných dat.

3. Pomocná funkce pro vygenerování bodů rozmístěných v soustředných kružnicích

Abychom si mohli ještě lépe ilustrovat principiální omezení algoritmu K-means, vyzkoušíme si použití odlišných metod generování vstupních bodů v ploše. Namísto nám již velmi dobře známé funkce make_blobs se pokusíme využít funkci nazvanou make_circles. Jedná se o příhodný název, protože výsledek skutečně připomíná soustředné kružnice. Tuto funkci lze zavolat následovně:

samples, labels = make_circles(
    n_samples=n_samples, factor=0.5, noise=0.05
)

kde parametr factor určuje rozdíl velikostí vnější a vnitřní kružnice a parametrem noise se nastavuje směrodatná odchylka při výpočtu pozice bodů.

Takto vypadá skript, který vygeneruje a následně zobrazí sadu bodů v rovině:

# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
 
from sklearn.datasets import make_circles
 
# testovací data
n_samples = 2000
 
samples, labels = make_circles(
    n_samples=n_samples, factor=0.5, noise=0.05
)
 
samples = samples[:, ::-1]
 
# vykreslení bodů v rovině
plt.scatter(samples[:, 0], samples[:, 1], s=1.0)
 
# uložení grafu do souboru
plt.savefig("circles1.png")
 
# vykreslení na obrazovku
plt.show()

Z výsledků je patrné, že shluková analýza založená na centroidech nemůže vypočítat ucházející výsledek:

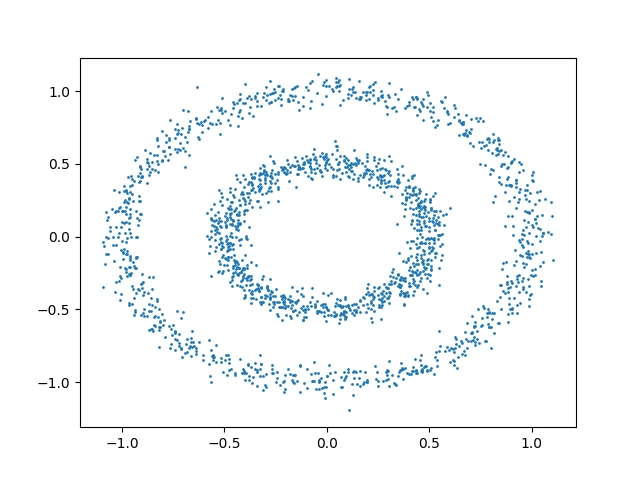
Obrázek 3: Body rozmístěné po ploše funkcí make_circles s použitím malé míry náhodnosti.

Pokusme se nyní zvýšit směrodatnou odchylku a zjistit, jak se tato změna projeví ve výsledném obrazci složeném z bodů:

# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
 
from sklearn.datasets import make_circles
 
# testovací data
n_samples = 2000
 
samples, labels = make_circles(
    n_samples=n_samples, factor=0.5, noise=0.10
)
 
samples = samples[:, ::-1]
 
# vykreslení bodů v rovině
plt.scatter(samples[:, 0], samples[:, 1], s=1.0)
 
# uložení grafu do souboru
plt.savefig("circles2.png")
 
# vykreslení na obrazovku
plt.show()

Obě kružnice již nebudou tak výrazné, takže je možné předpokládat, že i algoritmy pro shlukovou analýzu začnou mít s podobnými obrázky problémy:

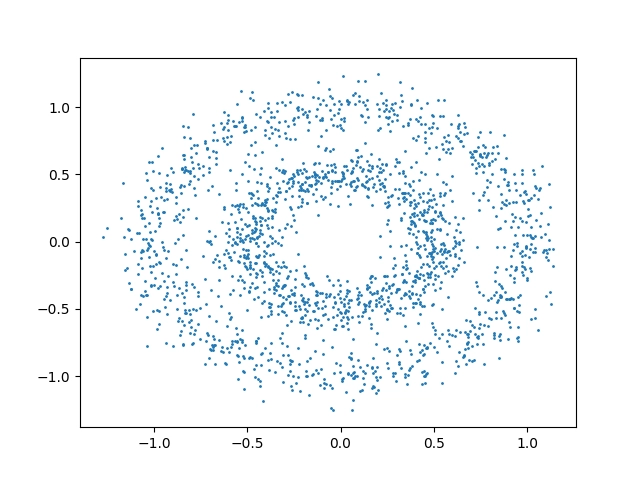
Obrázek 4: Body rozmístěné po ploše funkcí make_circles s použitím velké míry náhodnosti.

4. Pomocná funkce pro vygenerování bodů rozmístěných do dvou půlměsíců

Podobným způsobem si lze nechat vygenerovat sadu bodů, které po svém zobrazení v rovině vytvoří dvojici půlměsíců. Pro tento účel se používá funkce nazvaná make_moons:

samples, labels = make_moons(
    n_samples=n_samples, noise=0.05
)

Příklad použití této funkce:

# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
 
from sklearn.datasets import make_moons
 
# testovací data
n_samples = 2000
 
samples, labels = make_moons(
    n_samples=n_samples, noise=0.05
)
 
samples = samples[:, ::-1]
 
# vykreslení bodů v rovině
plt.scatter(samples[:, 0], samples[:, 1], s=1.0)
 
# uložení grafu do souboru
plt.savefig("moons1.png")
 
# vykreslení na obrazovku
plt.show()

Z výsledků je opět zřejmé, že klasický algoritmus pro clustering na základě nalezených centroidů zde nebude ideálním prostředkem pro shlukovou analýzu:

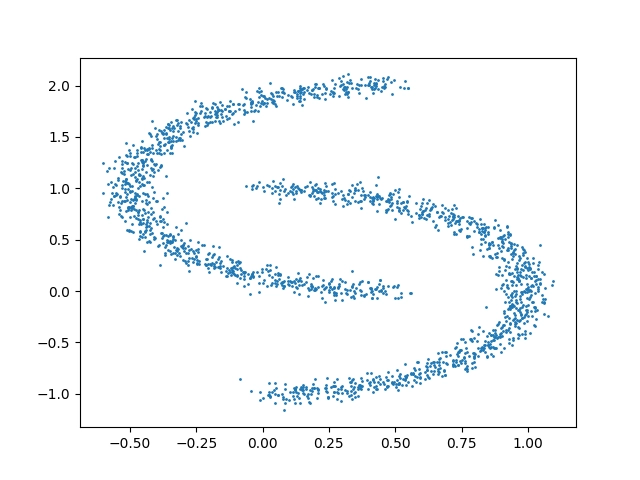
Obrázek 5: Body rozmístěné po ploše funkcí make_moons s použitím malé míry náhodnosti.

A pro úplnost ještě zvýšíme hodnotu směrodatné odchylky, což celý výsledný obrazec složený z bodů učiní ještě více náhodným:

# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
 
from sklearn.datasets import make_moons
 
# testovací data
n_samples = 2000
 
samples, labels = make_moons(
    n_samples=n_samples, noise=0.15
)
 
samples = samples[:, ::-1]
 
# vykreslení bodů v rovině
plt.scatter(samples[:, 0], samples[:, 1], s=1.0)
 
# uložení grafu do souboru
plt.savefig("moons2.png")
 
# vykreslení na obrazovku
plt.show()

Výsledný korelační diagram bude v tomto případě vypadat následovně:

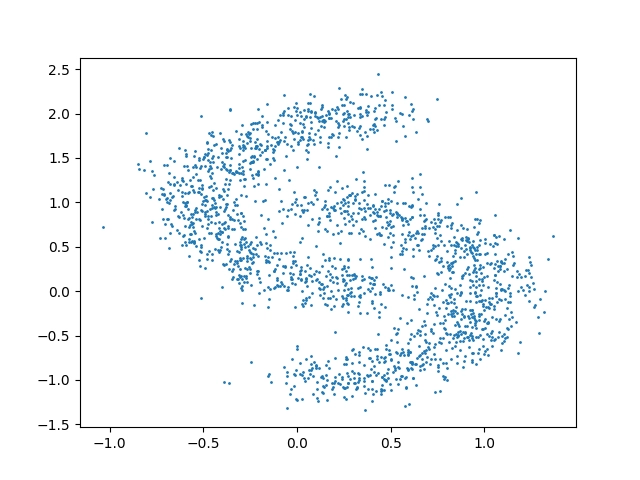
Obrázek 6: Body rozmístěné po ploše funkcí make_moons s použitím velké míry náhodnosti.

5. Shluková analýza algoritmem K-means pro body rozmístěné do soustředných kružnic

Vyzkoušejme si nyní, jak bude vypadat výsledek shlukové analýzy v případě, že na body vygenerované pomocnou funkcí make_circles (tedy na dvojici soustředných kružnic) použijeme algoritmus K-means, s nímž jsme se setkali v předchozím článku. Vygenerujeme celkem 2000 bodů a pousíme se najít 6 clusterů (i když počet nebude hrát velkou roli):

# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
 
from sklearn.cluster import KMeans
from sklearn.datasets import make_circles
 
# testovací data
n_samples = 2000
 
samples, labels = make_circles(
    n_samples=n_samples, factor=0.5, noise=0.05
)
 
samples = samples[:, ::-1]
 
plt.figure(1)
colors = ["#4444cc", "#44bb44", "#cc4444", "#cccc44", "#44cccc", "#cc44cc"]
 
# clustering
kmeans = KMeans(n_clusters=6, random_state=0, n_init="auto").fit(samples)
 
# vykreslení bodů s jejich přiřazením ke clusteru
for i, color in enumerate(colors):
    selector = kmeans.labels_ == i
    plt.scatter(samples[selector, 0], samples[selector, 1], c=color, marker=".", s=1)
 
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], c="red", s=50)
plt.title("K-Means++")
 
# uložení grafu do souboru
plt.savefig("circles_kmeans.png")
 
# vykreslení na obrazovku
plt.show()

Z výsledků je patrné to, co jsme pravděpodobně již tušili – algoritmus, který se snaží nalézt centroidy, bude prakticky nepoužitelný na body seskupené do dvojice soustředných kružnic, neboť takový tvar nelze tímto algoritmem rozumně rozdělit:

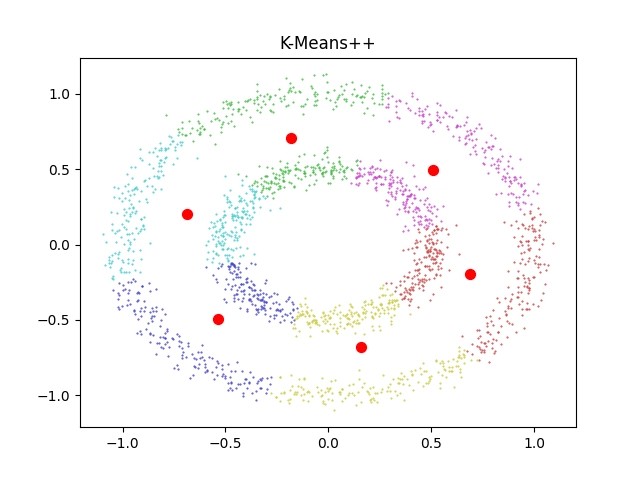
Obrázek 7: Výsledek shlukové analýzy provedené algoritmem K-means.

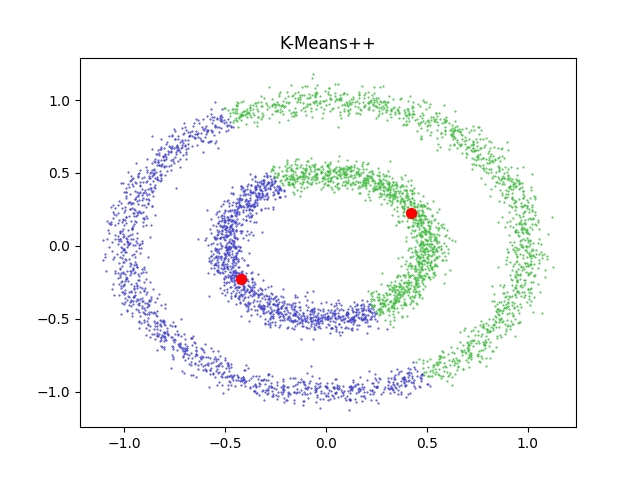
Obrázek 8: Výsledek pro 5000 vstupních bodů a dva výsledné clustery.

6. Shluková analýza algoritmem k-means pro body rozmístěné do dvou půlměsíců

Podobně ovšem platí, že algoritmus K-means nebude použitelný ani v případě, že mu předložíme body uspořádané do dvou půlměsíců, které navíc (alespoň částečně) do sebe zapadají. Opět si to ukažme na příkladu, v němž funkci make_circles nahradíme za funkci make_moons. Ve skriptu je specifikováno, že se body mají rozdělit do šesti clusterů, ovšem sami si můžete otestovat, že výsledky nebudou lepší ani při specifikaci dvou clusterů (což opět plyne z vlastností algoritmu K-means):

# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
 
from sklearn.cluster import KMeans
from sklearn.datasets import make_moons
 
# testovací data
n_samples = 2000
 
samples, labels = make_moons(
    n_samples=n_samples, noise=0.05
)
 
samples = samples[:, ::-1]
 
plt.figure(1)
colors = ["#4444cc", "#44bb44", "#cc4444", "#cccc44", "#44cccc", "#cc44cc"]
 
# clustering
kmeans = KMeans(n_clusters=6, random_state=0, n_init="auto").fit(samples)
 
# vykreslení bodů s jejich přiřazením ke clusteru
for i, color in enumerate(colors):
    selector = kmeans.labels_ == i
    plt.scatter(samples[selector, 0], samples[selector, 1], c=color, marker=".", s=1)
 
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], c="red", s=50)
plt.title("K-Means++")
 
# uložení grafu do souboru
plt.savefig("moons_kmeans.png")
 
# vykreslení na obrazovku
plt.show()

Výsledky:

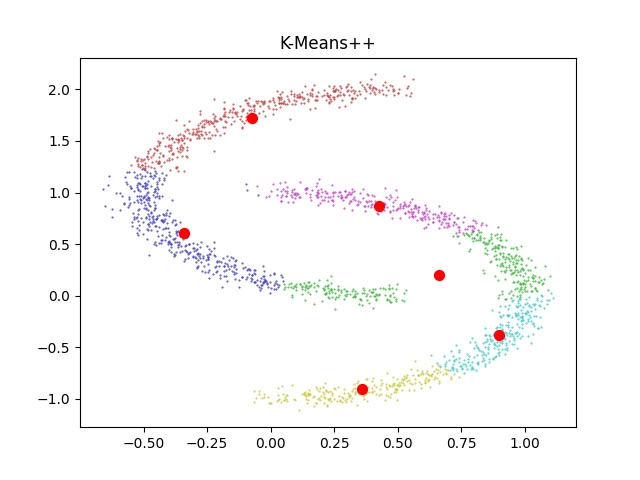
Obrázek 9: Výsledek shlukové analýzy provedené algoritmem K-means.

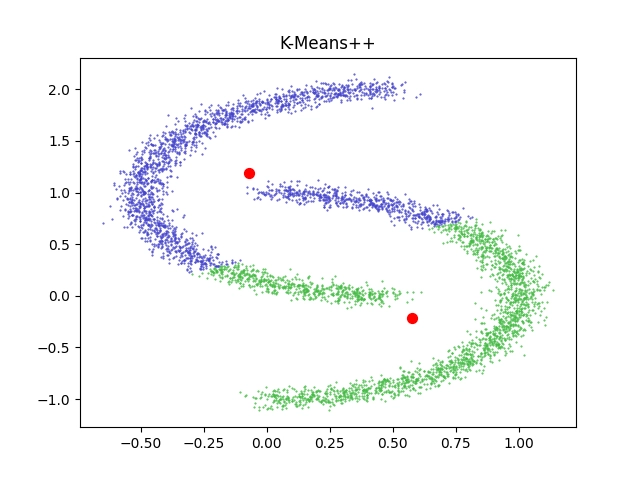
Obrázek 10: Výsledek pro 5000 vstupních bodů a dva clustery.

7. Shluková analýza realizovaná algoritmem spectral clustering

Z předchozích kapitol je patrné, že algoritmus K-means nedokáže provést korektní shlukovou analýzu ani pro body uspořádané do soustředných kružnic ani pro body uspořádané do dvou půlměsíců. Je to očekávatelné chování – ostatně ony dva tvary byly schválně zvoleny tak, aby nebyly algoritmem K-means řešitelné. Ovšem co použít namísto tohoto algoritmu? Knihovna Scikit-learn nám nabízí hned několik alternativních algoritmů, které se od sebe odlišují jak svými základními vlastnostmi (jaké tvary clusterů dokážou detekovat a zda dokáží pracovat s hierarchickými clustery), tak i časovou a prostorovou složitostí (tedy tím, kolik času procesoru, popř. jakou kapacitu operační paměti vyžadují).

Jedním z vhodných algoritmů je algoritmus nazvaný spectral clustering, jehož popis nalezneme například na této stránce. Shlukovou analýzu s využitím tohoto algoritmu provedeme příkazem:

spectral = SpectralClustering(n_clusters=n_components, eigen_solver="arpack", affinity="nearest_neighbors", random_state=0).fit(samples)

Vstupními parametry je především očekávaný počet clusterů (zde použijeme hodnotu 2) a parametr určující, jak bude zkonstruována matice příbuzných bodů. Navíc je možné pro velký počet bodů změnit způsob výpočtu vlastních čísel (eigenvalues) a použít tak sice rychlejší, ale v některých případech méně stabilní postup (oba dva poslední parametry si ještě otestujeme později).

8. Výsledek shlukové analýzy provedené algoritmem spectral clustering

Nyní nastává okamžik otestování základních vlastností algoritmu spectral clustering. Nejprve tento algoritmus vyzkoušíme nad body získanými pomocnou funkcí make_blobs. Mimochodem – povšimněte si, že analyzujeme množinu 10000 bodů, což se již (společně s požadovaným počtem nalezených clusterů) projeví na delší době běhu skriptu. Velká část výpočtů bude navíc provedena v jediném vláknu, což je problematika, ke které se ještě vrátíme:

# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
 
from sklearn.cluster import SpectralClustering
from sklearn.datasets import make_blobs
 
# testovací data
n_samples = 10000
 
# počet oblastí, kam se budou data sdružovat
n_components = 6
 
samples, labels = make_blobs(
    n_samples=n_samples, centers=n_components, cluster_std=1.50, random_state=0
)
 
samples = samples[:, ::-1]
 
plt.figure(1)
colors = ["#4444cc", "#44bb44", "#cc4444", "#cccc44", "#44cccc", "#cc44cc"]
 
# clustering
spectral = SpectralClustering(n_clusters=n_components, eigen_solver="arpack", affinity="nearest_neighbors", random_state=0).fit(samples)
 
# vykreslení bodů s jejich přiřazením ke clusteru
for i, color in enumerate(colors):
    selector = spectral.labels_ == i
    plt.scatter(samples[selector, 0], samples[selector, 1], c=color, marker=".", s=1)
 
plt.title("Spectral clustering")
 
# uložení grafu do souboru
plt.savefig("blobs_spectral.png")
 
# vykreslení na obrazovku
plt.show()

A takto bude vypadat rozdělení bodů do clusterů:

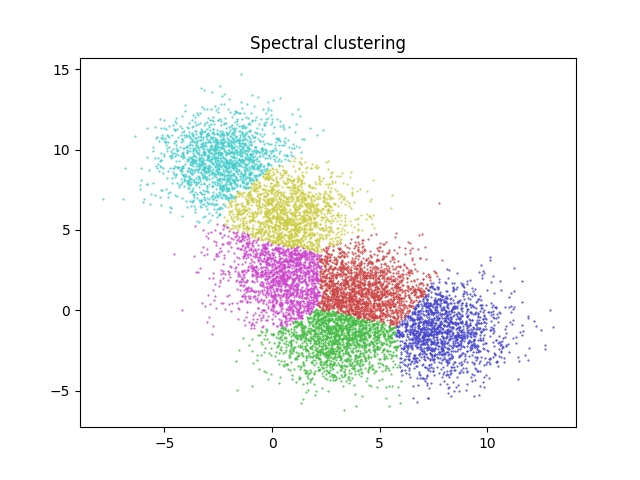
Obrázek 11: Výsledek shlukové analýzy provedené algoritmem Spectral clustering.

9. Shluková analýza algoritmem spectral clustering pro body rozmístěné do soustředných kružnic

Stejný algoritmus nyní použijeme pro shlukovou analýzu bodů rozmístěných (resp. vygenerovaných) pomocnou funkcí make_circles. Upravíme tedy celý skript následujícím způsobem (budeme pochopitelně vyžadovat nalezení dvou clusterů a nikoli šesti clusterů, jako tomu bylo v předchozí kapitole):

# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
 
from sklearn.cluster import SpectralClustering
from sklearn.datasets import make_circles
 
# testovací data
n_samples = 2000
 
samples, labels = make_circles(
    n_samples=n_samples, factor=0.5, noise=0.05
)
 
samples = samples[:, ::-1]
 
plt.figure(1)
colors = ["#4444cc", "#44bb44", "#cc4444", "#cccc44", "#44cccc", "#cc44cc"]
 
# clustering
spectral = SpectralClustering(n_clusters=2, eigen_solver="arpack", affinity="nearest_neighbors", random_state=0).fit(samples)
 
# vykreslení bodů s jejich přiřazením ke clusteru
for i, color in enumerate(colors):
    selector = spectral.labels_ == i
    plt.scatter(samples[selector, 0], samples[selector, 1], c=color, marker=".", s=1)
 
plt.title("Spectral clustering")
 
# uložení grafu do souboru
plt.savefig("circles_spectral.png")
 
# vykreslení na obrazovku
plt.show()

Nyní je zřejmé, že algoritmus správně rozpoznal a rozdělil body do dvou skupin. Na rozdíl od algoritmu K-means jsme tedy v tomto konkrétním případě získali použitelný výsledek:

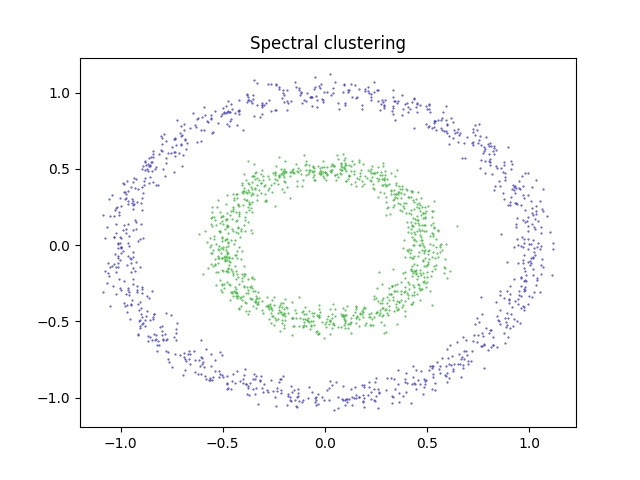
Obrázek 12: Výsledek shlukové analýzy provedené algoritmem Spectral clustering.

10. Shluková analýza algoritmem spectral clustering pro body rozmístěné do dvou půlměsíců

A konečně si otestujme, jak dobře (či naopak špatně) dokáže algoritmus spectral clustering rozdělit body, které jsou rozmístěné do oblastí připomínajících dva půlměsíce. Prozatím při vytváření vstupních bodů ponecháme hodnotu noise na relativně nízké hodnotě 0,05; později si vyzkoušíme tuto hodnotu postupně zvyšovat. A samozřejmě budeme vyžadovat rozdělení bodů do dvou clusterů:

# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
 
from sklearn.cluster import SpectralClustering
from sklearn.datasets import make_moons
 
# testovací data
n_samples = 2000
 
samples, labels = make_moons(
    n_samples=n_samples, noise=0.05
)
 
samples = samples[:, ::-1]
 
plt.figure(1)
colors = ["#4444cc", "#44bb44", "#cc4444", "#cccc44", "#44cccc", "#cc44cc"]
 
# clustering
spectral = SpectralClustering(n_clusters=2, eigen_solver="arpack", affinity="nearest_neighbors", random_state=0).fit(samples)
 
# vykreslení bodů s jejich přiřazením ke clusteru
for i, color in enumerate(colors):
    selector = spectral.labels_ == i
    plt.scatter(samples[selector, 0], samples[selector, 1], c=color, marker=".", s=1)
 
plt.title("Spectral clustering")
 
# uložení grafu do souboru
plt.savefig("moons_spectral.png")
 
# vykreslení na obrazovku
plt.show()

Výsledek zobrazený na následujícím obrázku opět naznačuje, že byl algoritmus pro danou vstupní množinu bodů velmi úspěšný:

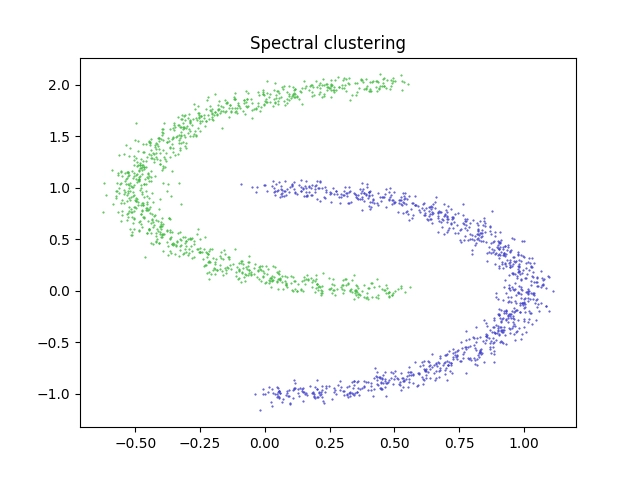
Obrázek 13: Výsledek shlukové analýzy provedené algoritmem Spectral clustering.

11. Meze algoritmu spectral clustering

Podobně jako v případě již minule popsaného algoritmu K-means má i algoritmus spectral clustering určité meze, které znamenají, že ho není možné použít ve všech případech (resp. přesněji řečeno můžeme získat shluky, které nebudou vyhovující). Zkusme jednu takovou mez objevit. Skript z předchozí kapitoly nepatrně upravíme tak, aby byly body tvořící vstupní data rozmístěny po větší ploše. To se provede snadno – zvýšením parametru noise z hodnoty 0.05 na hodnotu 0.15:

# testovací data
n_samples = 3000
 
samples, labels = make_moons(
    n_samples=n_samples, noise=0.15
)

Po této zdánlivě nepatrné úpravě již nebudou shluky (clustery) nalezené algoritmem spectral clustering ideální, což je ostatně velmi dobře patrné při pohledu na vizualizovaný výsledek. Algoritmus totiž za těchto podmínek již nedokázal správně rozpoznat oba více či méně izolované půlměsíce:

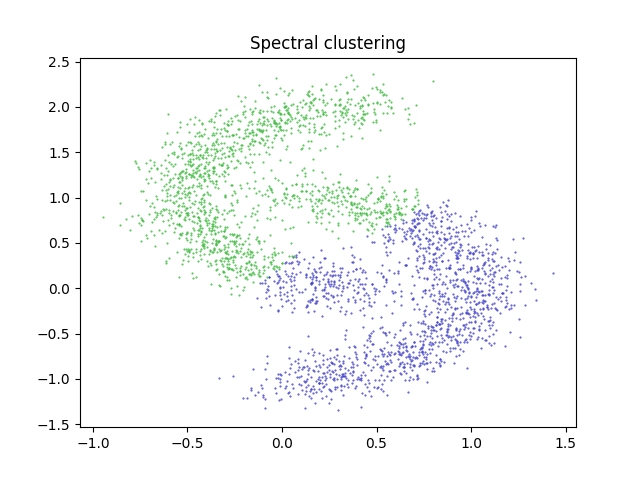
Obrázek 14: Výsledek shlukové analýzy provedené algoritmem Spectral clustering pro náhodněji rozmístěné body.

Výše zobrazený obrázek s vizualizací clusterů byl získán tímto skriptem:

# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
 
from sklearn.cluster import SpectralClustering
from sklearn.datasets import make_moons
 
# testovací data
n_samples = 3000
 
samples, labels = make_moons(
    n_samples=n_samples, noise=0.15
)
 
samples = samples[:, ::-1]
 
plt.figure(1)
colors = ["#4444cc", "#44bb44", "#cc4444", "#cccc44", "#44cccc", "#cc44cc"]
 
# clustering
spectral = SpectralClustering(n_clusters=2, eigen_solver="arpack", affinity="nearest_neighbors", random_state=0).fit(samples)
 
# vykreslení bodů s jejich přiřazením ke clusteru
for i, color in enumerate(colors):
    selector = spectral.labels_ == i
    plt.scatter(samples[selector, 0], samples[selector, 1], c=color, marker=".", s=1)
 
plt.title("Spectral clustering")
 
# uložení grafu do souboru
plt.savefig("moons_spectral.png")
 
# vykreslení na obrazovku
plt.show()

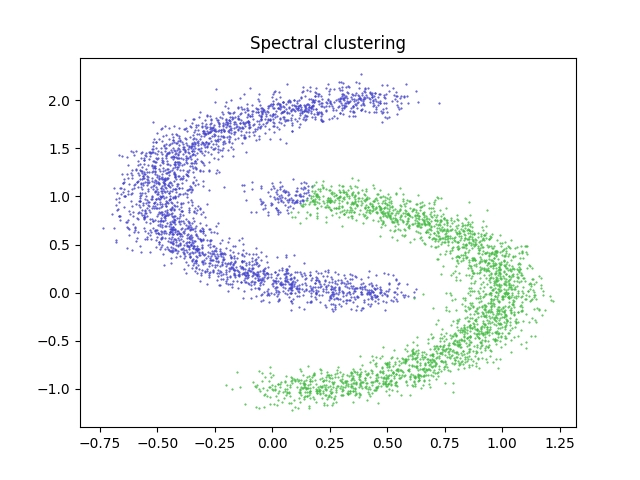
Obrázek 15: Pro 5000 bodů leží mez použitelnosti algoritmu na hodnotě noise přibližně 0,8 či 0,9. Zde již můžeme vidět špatné rozdělení bodů do clusterů.

12. Další algoritmy shlukové analýzy nabízené knihovnou Scikit-Learn

Pro oba zmíněné „problematické“ tvary (resp. přesněji řečeno oblasti, v níž jsou vstupní body generovány) lze s úspěchem použít tyto algoritmy:

• spectral clustering (již jsme si vyzkoušeli)
• DBSCAN
• HDBSCAN
• OPTICS

K základním vlastnostem tří zbylých algoritmů se ještě vrátíme, protože v praxi je důležité pro každý problém vybrat ten správný algoritmus a navíc i korektně nastavit jeho parametry (což se mnohdy musí provádět iterativním způsobem).

13. Emergence: struktury vzniklé ze zdánlivého chaosu

V některých dynamických systémech mohou i na základě mnohdy velmi jednoduchých pravidel vznikat složitější emergentní struktury. Tato vlastnost se týká mnoha typů komplexních systémů, ovšem nás budou v dnešním (i v navazujícím) článku zajímat především takové komplexní systémy, v nichž je možné vlastnosti jejich jednotlivých elementů reprezentovat jako body v ploše či v prostoru.

Poměrně známým příkladem mohou být různé systémy částic (particle systems), v nichž lze při vhodné definici pravidel chování jednotlivých částic taktéž nalézt emergentní struktury. Toto téma je sice velmi rozsáhlé a vyžádá si nejméně jeden samostatný článek, ovšem již dnes si můžeme jeden takový částicový systém ukázat. A vzhledem k tomu, že dále zmíněný částicový systém vede ke vzniku emergentní struktury (a nikoli pouze náhodného „oblaku“ bodů), budeme ho moci analyzovat právě s využitím shlukové analýzy.

14. Příklad vzniku emergentní struktury

Vlastní částicový systém, který budeme modelovat, je vlastně poměrně jednoduchý. Nachází se v něm čtyři typy částic, které se při vykreslování liší svou barvou. Částice se pohybují v rovině a působí na ně jak setrvačnost, tak i vzájemná přitažlivost. Ovšem nejzajímavější je, že přitažlivost mezi různými kombinacemi částic může být taktéž rozdílná – tedy například dvě červené částice se budou přitahovat jinou silou, než dvě stejně vzdálené částice s červenou a žlutou barvou atd. A právě modifikací počtu částic různé barvy a obsahu matice s koeficienty přitažlivosti (což jsou vlastně gravitační konstanty) částic různých barev lze dosáhnout mnohdy i velmi komplexního chování celého systému – budou se tvořit organické tvary, vzniknou „predátoři“ z několika částic stejné barvy, vznikne stabilní mřížce podobná struktura atd.

Realizace takového systému v Pythonu je sice z pohledu programátora snadná, ovšem samotná simulace bude velmi pomalá (zejména v porovnání s céčkovou variantou, kterou mám taktéž k dispozici). Důležité však je, že klávesou w lze v libovolném okamžiku simulace uložit pozice všech částic do souboru ve formátu CSV:

# vim: set fileencoding=utf-8
 
import sys
from enum import Enum
from random import random
from math import sqrt
 
import pygame
import pygame.locals
 
WINDOW_WIDTH = 800
WINDOW_HEIGHT = 600
WINDOW_TITLE = "Particle life simulator"
 
# Constants used by model
RED_GROUP = 0
GREEN_GROUP = 1
YELLOW_GROUP = 2
BLUE_GROUP = 3
 
# Model options
BORDER = 50
 
# Number of particles of different colors/attributes
MAX_RED = 1000
MAX_GREEN = 200
MAX_BLUE = 50
MAX_YELLOW = 10
 
# Total number of particles in the whole system
MAX_PARTICLES = MAX_RED+MAX_GREEN+MAX_BLUE+MAX_YELLOW
 
# Other model options
MAX_DISTANCE = 2000
DAMPING_FACTOR = 0.5
SLOW_DOWN_FACTOR = 0.1
SCALE_FACTOR = 1
 
 
class Colors(Enum):
    """Named colors used everywhere on demo screens."""
 
    BLACK = (0, 0, 0)
    BLUE = (0, 0, 255)
    CYAN = (0, 255, 255)
    GREEN = (0, 255, 0)
    YELLOW = (255, 255, 0)
    RED = (255, 0, 0)
    MAGENTA = (255, 0, 255)
    WHITE = (255, 255, 255)
 
 
class Particle:
    def __init__(self, x : float, y : float, vx : float, vy : float, type : int):
        self.x = x
        self.y = y
        self.vx = vx
        self.vy = vy
        self.type = type
 
 
class Atoms:
    def __init__(self, max_particles : int):
        self.colors = (0xffff0000, 0xff00ff00, 0xff2020ff, 0xffffff00)
        self.particles = []
        self.particles += (create_particles(MAX_RED, RED_GROUP))
        self.particles += (create_particles(MAX_GREEN, GREEN_GROUP))
        self.particles += (create_particles(MAX_BLUE, BLUE_GROUP))
        self.particles += (create_particles(MAX_YELLOW, YELLOW_GROUP))
        print("Particles in atoms:", len(self.particles))
 
 
class Model:
    def __init__(self, max_particles : int):
        self.rules = [[0,0,0,0], [0,0,0,0], [0,0,0,0], [0,0,0,0]]
        self.init_rules()
        self.atoms = Atoms(max_particles)
 
    def init_rules(self):
        for j in range(4):
            for i in range(4):
                self.rules[i][j] = 2.0*random() - 1.0
 
 
def random_x() -> float:
    return (WINDOW_WIDTH - BORDER*2) * random() + BORDER
 
 
def random_y() -> float:
    return (WINDOW_HEIGHT - BORDER*2) * random() + BORDER
 
 
def create_particles(max : int, type : int):
    return [Particle(random_x(), random_y(), 0.0, 0.0, type) for i in range(max)]
 
 
def redraw(surface, model):
    surface.fill(Colors.BLACK.value)
    atoms = model.atoms
    for particle in atoms.particles:
        color = atoms.colors[particle.type]
        surface.set_at((int(particle.x),int(particle.y)), color)
        surface.set_at((int(particle.x-1),int(particle.y)), color)
        surface.set_at((int(particle.x+1),int(particle.y)), color)
        surface.set_at((int(particle.x),int(particle.y-1)), color)
        surface.set_at((int(particle.x),int(particle.y+1)), color)
 
 
def apply_rules(model : Model):
    for i in range(len(model.atoms.particles)):
        fx : float = 0.0
        fy : float = 0.0
 
        a = model.atoms.particles[i]
 
        # compute force for selected particle
        for j in range(len(model.atoms.particles)):
            if i != j:
                b = model.atoms.particles[j]
                g = model.rules[a.type][b.type] * SCALE_FACTOR
                dx = a.x - b.x
                dy = a.y - b.y
                if dx != 0.0 or dy != 0.0:
                    d = dx*dx + dy*dy
                    if d < MAX_DISTANCE:
                        f = g / sqrt(d)
                        fx += f * dx
                        fy += f * dy
 
        # apply force to selected particle
        a.vx = (a.vx + fx) * DAMPING_FACTOR
        a.vy = (a.vy + fy) * DAMPING_FACTOR
 
        # move particle
        a.x += a.vx
        a.y += a.vy
 
        # check if particle touches scene boundary
        if a.x <= 0:
            a.vx = -a.vx
            a.x = 0
 
        if a.x >= WINDOW_WIDTH:
            a.vx = -a.vx
            a.x = WINDOW_WIDTH - 1
 
        if a.y <= 0:
            a.vy = -a.vy
            a.y = 0
 
        if a.y >= WINDOW_HEIGHT:
            a.vy = -a.vy
            a.y = WINDOW_HEIGHT - 1
 
 
def write_particles(model, filename):
    atoms = model.atoms
    with open(filename, "w") as fout:
        fout.write('"x","y"\n')
        for particle in atoms.particles:
            fout.write(f"{particle.x},{particle.y}\n")
 
 
# set window title
pygame.display.set_caption(WINDOW_TITLE)
 
display = pygame.display.set_mode([WINDOW_WIDTH, WINDOW_HEIGHT])
display.fill(Colors.BLACK.value)
 
surface = pygame.Surface([WINDOW_WIDTH, WINDOW_HEIGHT])
surface.set_at((101,100), 0xffff0000)
surface.set_at((100,101), 0xffff0000)
surface.set_at((101,101), 0xffff0000)
 
clock = pygame.time.Clock()
model = Model(MAX_PARTICLES)
 
while True:
    for event in pygame.event.get():
        if event.type == pygame.locals.QUIT:
            pygame.quit()
            sys.exit()
        if event.type == pygame.locals.KEYDOWN:
            if event.key == pygame.locals.K_ESCAPE:
                pygame.quit()
                sys.exit()
            if event.key == pygame.locals.K_RETURN:
                pygame.quit()
                sys.exit()
            if event.key == pygame.locals.K_w:
                write_particles(model, "particles.csv")
 
    # all events has been processed - update scene and redraw the screen
    apply_rules(model)
    redraw(surface, model)
    display.blit(surface, (0, 0))
    pygame.display.update()
    # clock.tick(25)

CSV soubor, který lze v libovolném čase simulace vygenerovat, si zobrazíme formou korelačního diagramu následujícím skriptem:

# budeme provádět vykreslování de facto standardní knihovnou Matplotlib
import matplotlib.pyplot as plt
 
# knihovnu Pandas využijeme pro načtení datového rámce
import pandas as pd
 
df = pd.read_csv("particles.csv")
 
# vykreslení bodů v rovině
plt.scatter(df["x"], df["y"], s=1)
 
# uložení grafu do souboru
plt.savefig("particles.png")
 
# vykreslení na obrazovku
plt.show()

Ve výsledku můžeme vidět zrod emergentní struktury.

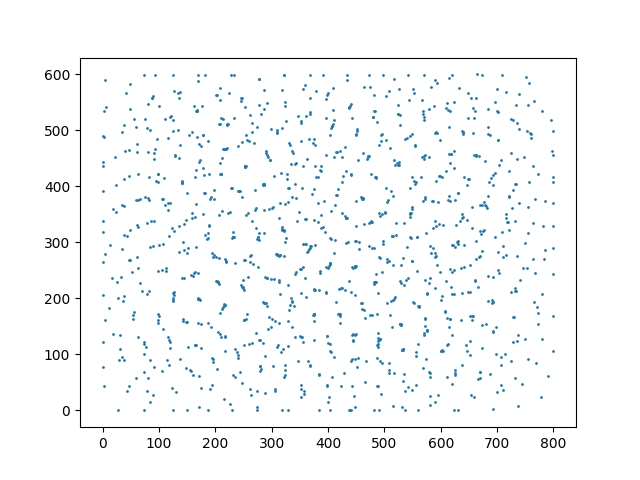
Obrázek 16: Emergentní struktura, která je výsledkem simulace.

15. Repositář s demonstračními příklady

Všechny demonstrační příklady využívající knihovnu Scikit-learn lze nalézt v repositáři https://github.com/tisnik/most-popular-python-libs. Následují odkazy na jednotlivé příklady i na (Jupyter) diáře s postupem výpočtů a analýz:

16. Odkazy na Internetu

1. scikit-learn: Machine Learning in Python
   https://scikit-learn.org/stable/index.html
2. Sklearn-pandas
   https://github.com/scikit-learn-contrib/sklearn-pandas
3. sklearn-xarray
   https://github.com/phausamann/sklearn-xarray/
4. Clustering
   https://scikit-learn.org/stable/modules/clus­tering.html
5. Cluster analysis (Wikipedia)
   https://en.wikipedia.org/wi­ki/Cluster_analysis
6. Shluková analýza (Wikipedia)
   https://cs.wikipedia.org/wi­ki/Shlukov%C3%A1_anal%C3%BDza
7. K-means
   https://cs.wikipedia.org/wiki/K-means
8. k-means clustering
   https://en.wikipedia.org/wiki/K-means_clustering
9. Spectral clustering
   https://en.wikipedia.org/wi­ki/Spectral_clustering
10. Emergence
    https://cs.wikipedia.org/wi­ki/Emergence
11. Particle Life: Vivid structures from rudimentary rules
    https://particle-life.com/
12. Hertzsprungův–Russellův diagram
    https://cs.wikipedia.org/wi­ki/Hertzsprung%C5%AFv%E2%80%93Rus­sell%C5%AFv_diagram
13. Using Machine Learning in an HR Diagram
    https://cocalc.com/share/pu­blic_paths/08b6e03583cbdef3cdb98­13a54ec68ff773c747f
14. Gaia H-R diagrams: Querying Gaia data for one million nearby stars
    https://vlas.dev/post/gaia-dr2-hrd/
15. The Hertzsprung–Russell diagram
    https://scipython.com/book2/chapter-9-data-analysis-with-pandas/problems/p92/the-hertzsprung-russell-diagram/
16. Animated Hertzsprung-Russell Diagram with 119,614 datapoints
    https://github.com/zonination/h-r-diagram
17. Neuraxle Pipelines
    https://github.com/Neuraxio/Neuraxle
18. scikit-learn: Getting Started
    https://scikit-learn.org/stable/getting_started.html
19. Support Vector Machines
    https://scikit-learn.org/stable/modules/svm.html
20. Use Deep Learning to Detect Programming Languages
    http://searene.me/2017/11/26/use-neural-networks-to-detect-programming-languages/
21. Natural-language processing
    https://en.wikipedia.org/wiki/Natural-language_processing
22. THE MNIST DATABASE of handwritten digits
    http://yann.lecun.com/exdb/mnist/
23. MNIST database (Wikipedia)
    https://en.wikipedia.org/wi­ki/MNIST_database
24. MNIST For ML Beginners
    https://www.tensorflow.or­g/get_started/mnist/begin­ners
25. Stránka projektu Torch
    http://torch.ch/
26. Torch: Serialization
    https://github.com/torch/tor­ch7/blob/master/doc/seria­lization.md
27. Torch: modul image
    https://github.com/torch/i­mage/blob/master/README.md
28. Data pro neuronové sítě
    http://archive.ics.uci.edu/ml/in­dex.php
29. Torch na GitHubu (několik repositářů)
    https://github.com/torch
30. Torch (machine learning), Wikipedia
    https://en.wikipedia.org/wi­ki/Torch_%28machine_learnin­g%29
31. Torch Package Reference Manual
    https://github.com/torch/tor­ch7/blob/master/README.md
32. Torch Cheatsheet
    https://github.com/torch/tor­ch7/wiki/Cheatsheet
33. Neural network containres (Torch)
    https://github.com/torch/nn/blob/mas­ter/doc/containers.md
34. Simple layers
    https://github.com/torch/nn/blob/mas­ter/doc/simple.md#nn.Line­ar
35. Transfer Function Layers
    https://github.com/torch/nn/blob/mas­ter/doc/transfer.md#nn.tran­sfer.dok
36. Feedforward neural network
    https://en.wikipedia.org/wi­ki/Feedforward_neural_net­work
37. Biologické algoritmy (4) – Neuronové sítě
    https://www.root.cz/clanky/biologicke-algoritmy-4-neuronove-site/
38. Biologické algoritmy (5) – Neuronové sítě
    https://www.root.cz/clanky/biologicke-algoritmy-5-neuronove-site/
39. Umělá neuronová síť (Wikipedia)
    https://cs.wikipedia.org/wi­ki/Um%C4%9Bl%C3%A1_neuronov%C3%A1_s%C3%AD%C5%A5
40. PyTorch
    http://pytorch.org/
41. JupyterLite na PyPi
    https://pypi.org/project/jupyterlite/
42. JupyterLite na GitHubu
    https://github.com/jupyter­lite/jupyterlite
43. Dokumentace k projektu JupyterLite
    https://github.com/jupyter­lite/jupyterlite
44. Matplotlib Home Page
    http://matplotlib.org/
45. Matplotlib (Wikipedia)
    https://en.wikipedia.org/wi­ki/Matplotlib
46. Popis barvových map modulu matplotlib.cm
    https://gist.github.com/en­dolith/2719900#id7
47. Ukázky (palety) barvových map modulu matplotlib.cm
    http://matplotlib.org/exam­ples/color/colormaps_refe­rence.html
48. Galerie grafů vytvořených v Matplotlibu
    https://matplotlib.org/3.2.1/gallery/