Obsah
1. Shluková analýza (clustering) a knihovna Scikit-learn (3D prostor)
2. Krátká odbočka: Lorenzův atraktor
3. Zobrazení Lorenzova atraktoru formou bodů propojených úsečkami
5. Pomocná metoda pro vygenerování sady bodů v 3D prostoru
6. Vygenerování sady 3D bodů s jejich vizualizací
7. Zvětšení směrodatné odchylky při generování bodů v 3D prostoru
8. Několik různých pohledů na body v 3D prostoru
9. Zobrazení skupiny 3D bodů ze tří směrů
10. Obarvení bodů na základě toho, do jakého clusteru patří
11. Nalezení centroidů a provedení shlukové analýzy algoritmem K-means
12. Algoritmus K-means a náhodněji rozmístěné body v prostoru
13. Algoritmus K-means a zcela náhodně rozmístěné body v prostoru
14. Časová náročnost algoritmu K-means
16. Zobrazení vlivu počtu bodů na rychlost algoritmu K-means
17. Repositář s demonstračními příklady
1. Shluková analýza (clustering) a knihovna Scikit-learn (3D prostor)
V úvodních dvou článcích [1] [2] o knihovně Scikit-learn a algoritmech shlukové analýzy, která tato knihovna datovým analytikům poskytuje, jsme se zaměřili na ty nejjednodušší případy. Konkrétně se jednalo o problémy, v nichž se vyskytují data, která lze v případě potřeby zobrazit v 2D prostoru (tedy například svítivost hvězdy a její barva atd.). Taková data jsme mohli snadno zobrazit formou bodů vynesených do takzvaného korelačního diagramu. A výsledkem shlukové analýzy (ať již byla provedena jakýmkoli algoritmem) je přiřazení indexu (čísla) clusteru každému takovému bodu ze vstupní množiny. Toto číslo můžeme převést na barvu a opět použít korelační diagram pro vizualizaci výsledků, tj. v tomto případě obarvených bodů v 2D prostoru. Výsledek je snadno pochopitelný a případné problematické chování algoritmu pro shlukovou analýzu můžeme relativně rychle odhalit.
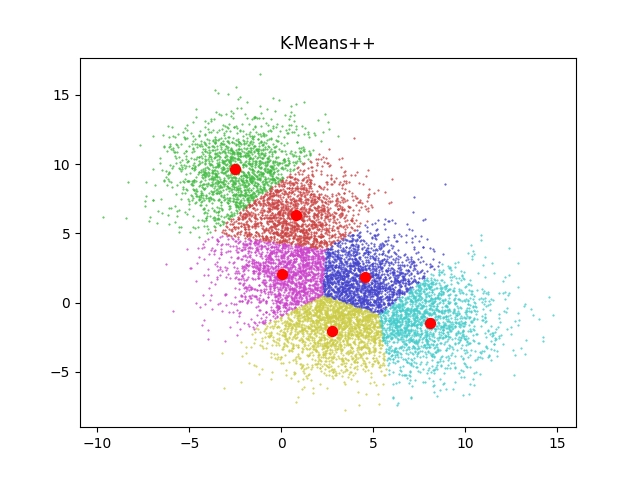
Obrázek 1: Výsledek shlukové analýzy pro překrývající se oblasti centroidů. Analýza byla provedena algoritmem K-means, který již známe.
Ovšem v případě, že data, která se mají analyzovat, mají vyšší dimenzionalitu (například se jedná o údaje o teplotě, vlhkosti a tlaku), je situace komplikovanější, protože sice můžeme na obrazovce vykreslit „3D graf“, ovšem stále se bude fyzicky jednat pouze o dvoudimenzionální obrázek, který trojdimenzionální prostor jen napodobuje. Můžeme si pomoci některými technikami – interaktivním natáčením grafu, zobrazením grafu ze tří (či šesti) směrů odpovídajících souřadným osám (nárys, půdorys, bokorys a jejich protějšky), projekcí grafu z několika směrů na plochy tvořené souřadnými osami atd. (což vlastně jinými slovy znamená – použijeme nějaký výpočet pro snížení počtu dimenzí). A navíc se budou komplikovat i samotné algoritmy pro shlukovou analýzu, protože přidání další dimenze (či dimenzí) není triviální ani v počítačové grafice, ani v matematice.
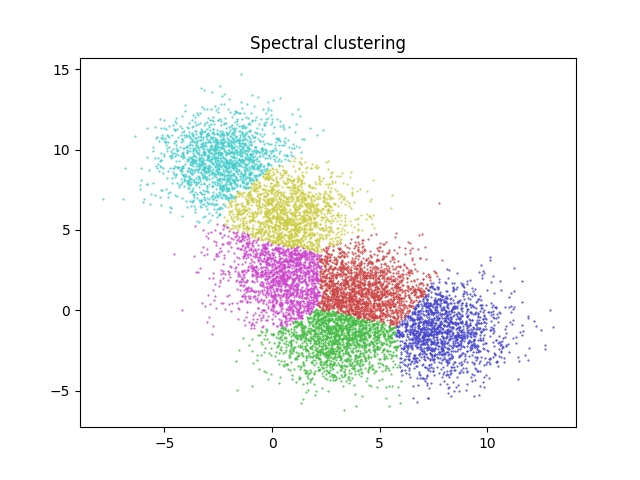
Obrázek 2: Výsledek shlukové analýzy provedené algoritmem Spectral clustering, a to opět na dvourozměrných vstupních datech.
2. Krátká odbočka: Lorenzův atraktor
Poměrně vděčným příkladem funkce zobrazené v 3D prostoru je dynamický systém s takzvaným podivným atraktorem, který je nazvaný Lorenzův atraktor podle svého objevitele. Tento systém sestávající ze tří dynamických rovnic použil Edward Lorenz v roce 1963 při simulaci vývoje počasí (resp. ve velmi zjednodušeném modelu počasí). Na tomto systému byla také numericky a analyticky ověřena velká citlivost na počáteční podmínky (někdy také nazývaná „motýlí efekt“).
Pro upřesnění je však nutné říci, že při simulaci na počítači vlastně získáme atraktor, jenž je periodický. Je tomu tak z toho důvodu, že pro zobrazení číselných hodnot je použito konečného počtu bitů, z toho nutně vyplývá, že se po určitém počtu kroků (který je však obrovský, takže tento jev mnohdy nezaregistrujeme) začne dráha Lorenzova atraktoru překrývat. V matematicky přesném modelu však tato situace nenastane, každá smyčka funkce bude mít unikátní tvar a dráhy se nebudou překrývat, pouze protínat.
Diferenciální rovnice Lorenzova atraktoru mají po převodu na diferenční tvar následující formát:
dx/dt = σ (y-x) dy/dt = x(ρ - z) - y dz/dt = xy - Βz
Takže pro iterativní (samozřejmě že nepřesný) výpočet můžeme pracovat s následujícími vztahy, které pro dostatečně malé dt vedou k výpočtu bodů ležících na Lorenzově atraktoru:
xn+1=xn+(σ (y-x)) dt yn+1=yn+(x(ρ - z) - y) dt zn+1=zn+(xy - Βz) dt
Podívejme se nyní na způsob implementace této funkce v Pythonu, což je snadné:
def lorenz(x, y, z, s=10, r=28, b=2.667):
x_dot = s*(y - x)
y_dot = r*x - y - x*z
z_dot = x*y - b*z
return x_dot, y_dot, z_dot
Následuje ukázka způsobu výpočtu sekvence bodů ležících na atraktoru:
# prozatím prázdné pole připravené pro výpočet
x = np.zeros((n,))
y = np.zeros((n,))
z = np.zeros((n,))
# počáteční hodnoty
x[0], y[0], z[0] = (0., 1., 1.05)
# vlastní výpočet atraktoru (resp. bodů na něm ležících)
for i in range(n-1):
x_dot, y_dot, z_dot = lorenz(x[i], y[i], z[i])
x[i+1] = x[i] + x_dot * dt
y[i+1] = y[i] + y_dot * dt
z[i+1] = z[i] + z_dot * dt
3. Zobrazení Lorenzova atraktoru formou bodů propojených úsečkami
Pro zobrazení průběhu reprezentovaného body vypočtenými na základě kódu z předchozí kapitoly můžeme použít následující postup:
- S využitím konstruktoru matplotlib.pyplot.figure získáme instanci třídy matplotlib.figure.Figure, což je kontejner pro vlastní grafy a diagramy.
- Metodou add_subplot do kontejneru přidáme graf (či diagram), což nám navíc umožní specifikovat způsob zobrazení (projekci). Výsledkem je instance třídy matplotlib.axes.Axes.
Celý výše zmíněný postup je realizován v následujícím pythonovském skriptu:
#!/usr/bin/env python
# Vykreslení Lorenzova atraktoru
import matplotlib.pyplot as plt
import numpy as np
# funkce pro výpočet dalšího bodu Lorenzova atraktoru
def lorenz(x, y, z, s=10, r=28, b=2.667):
x_dot = s * (y - x)
y_dot = r * x - y - x * z
z_dot = x * y - b * z
return x_dot, y_dot, z_dot
# krok (změna času)
dt = 0.01
# celkový počet vypočtených bodů na Lorenzově atraktoru
n = 10000
# prozatím prázdné pole připravené pro výpočet
x = np.zeros((n,))
y = np.zeros((n,))
z = np.zeros((n,))
# počáteční hodnoty
x[0], y[0], z[0] = (0.0, 1.0, 1.05)
# vlastní výpočet atraktoru
for i in range(n - 1):
x_dot, y_dot, z_dot = lorenz(x[i], y[i], z[i])
x[i + 1] = x[i] + x_dot * dt
y[i + 1] = y[i] + y_dot * dt
z[i + 1] = z[i] + z_dot * dt
# příprava 3D grafu
fig = plt.figure(figsize=(6.4, 6.4))
ax = fig.add_subplot(projection="3d")
# vykreslení grafu
ax.plot(x, y, z)
# uložení grafu do souboru
plt.savefig("lorenz_attractor.png")
# zobrazení grafu
plt.show()
Takto vypadá výsledek po vizualizaci nástrojem Matplotlib:
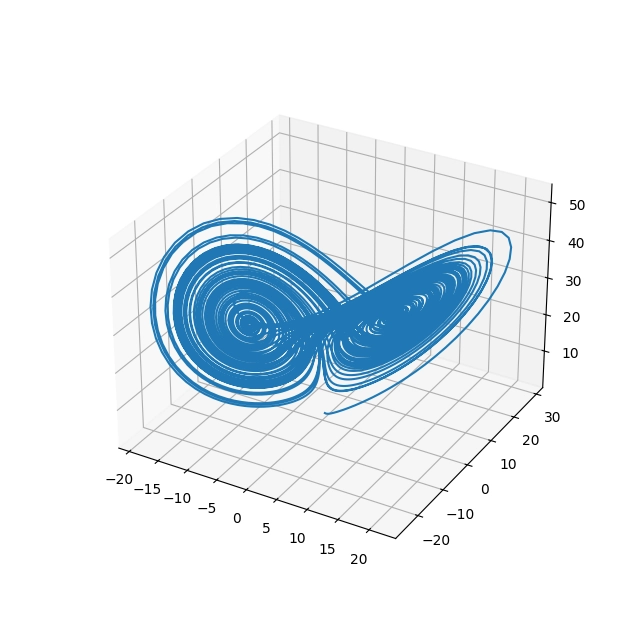
Obrázek 3: Lorenzův atraktor vykreslený formou bodů propojených úsečkami.
4. Lorenzův atraktor vykreslený formou jednotlivých bodů s definovaným stylem zobrazení a velikostí stopy
V dalších kapitolách budeme potřebovat v 3D grafu zobrazit jednotlivé body, nikoli body propojené úsečkami. Pro tento účel lze v knihovně Matplotlib použít několik způsobů (například lze upravit styl zobrazení u předchozího typu grafu), ovšem nejjednodušší a většinou i nejrychlejší je využít metodu matplotlib.axes.Axes.scatter, které se předají tři vektory s x-ovými, y-ovými a z-ovými souřadnicemi. Tvar jednotlivých bodů se specifikuje nepovinným parametrem marker a jejich velikost parametrem s. Upravený skript, který toto vykreslení provede, bude vypadat následovně:
#!/usr/bin/env python
# Vykreslení Lorenzova atraktoru
import matplotlib.pyplot as plt
import numpy as np
# funkce pro výpočet dalšího bodu Lorenzova atraktoru
def lorenz(x, y, z, s=10, r=28, b=2.667):
x_dot = s * (y - x)
y_dot = r * x - y - x * z
z_dot = x * y - b * z
return x_dot, y_dot, z_dot
# krok (změna času)
dt = 0.01
# celkový počet vypočtených bodů na Lorenzově atraktoru
n = 10000
# prozatím prázdné pole připravené pro výpočet
x = np.zeros((n,))
y = np.zeros((n,))
z = np.zeros((n,))
# počáteční hodnoty
x[0], y[0], z[0] = (0.0, 1.0, 1.05)
# vlastní výpočet atraktoru
for i in range(n - 1):
x_dot, y_dot, z_dot = lorenz(x[i], y[i], z[i])
x[i + 1] = x[i] + x_dot * dt
y[i + 1] = y[i] + y_dot * dt
z[i + 1] = z[i] + z_dot * dt
# příprava 3D grafu
fig = plt.figure(figsize=(6.4, 6.4))
ax = fig.add_subplot(projection="3d")
# vykreslení grafu
ax.scatter(x, y, z, marker=".", s=1)
# uložení grafu do souboru
plt.savefig("lorenz_attractor_2.png")
# zobrazení grafu
plt.show()
Podívejme se na výsledek získaný po spuštění tohoto skriptu:
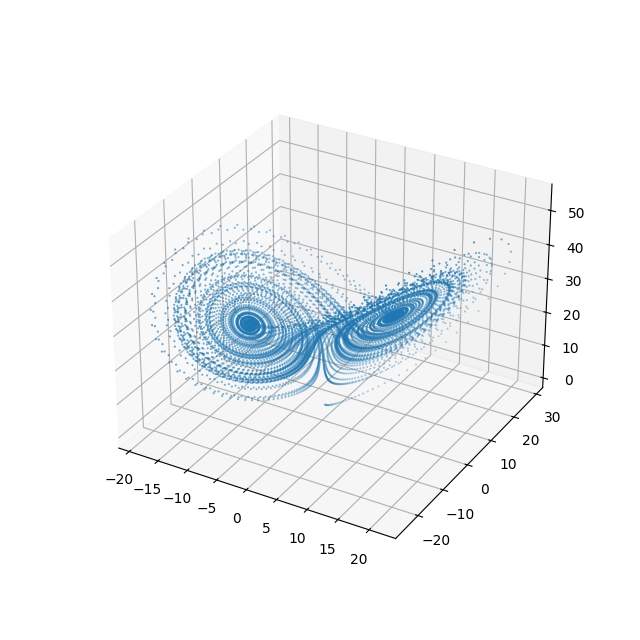
Obrázek 4: Lorenzův atraktor vykreslený formou jednotlivých bodů s definovaným stylem zobrazení a velikostí stopy.
5. Pomocná metoda pro vygenerování sady bodů v 3D prostoru
Pro další pokusy budeme potřebovat získat vhodnou sadu bodů rozmístěných v 3D prostoru. Ovšem je nutné, aby tyto body nebyly rozmístěny zcela náhodně (tam poněkud postrádá shluková analýza smysl). Existuje relativně velké množství způsobů a algoritmů, jak body v prostoru rozmístit. V dalších kapitolách použijeme funkci, kterou již dobře známe. Jedná se o funkci nazvanou sklearn.datasets.make_blobs, která nejprve vybere n centrálních bodů a poté rozmisťuje další body okolo těchto center tak, že pravděpodobnost umístění bodu dále od centra klesá podle Gaussovy křivky (teoreticky tedy může být bod umístěn v prostoru kdekoli, ovšem s větší vzdáleností od centrálních bodů pravděpodobnost jeho umístění do daného místa klesá – což si ověříme vizuálně).
Minule i předminule jsme funkcí sklearn.datasets.make_blobs vytvořili sadu bodů v rovině. Aby se generovaly 3D souřadnice (popř. i souřadnice do n-dimenzionálního prostoru), je nutné této funkci mj. předat i parametr n_features s požadovaným počtem souřadnic pro každý bod:
samples, labels = make_blobs(
n_samples=n_samples, n_features=3, centers=n_components,
cluster_std=0.80, random_state=0
)
6. Vygenerování sady 3D bodů s jejich vizualizací
Nyní již máme k dispozici všechny potřebné znalosti proto, abychom si nechali vygenerovat sadu bodů v prostoru, které se budou shlukovat okolo několika center (bude jich celkem osm, ovšem samozřejmě se jedná o konfigurovatelný parametr) a následně jsme si mohli tyto body zobrazit na grafu. Celý postup je realizován v tomto skriptu:
#!/usr/bin/env python
# Vykreslení bodů v 3D prostoru
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
# celkový počet vypočtených bodů
n_samples = 10000
# počet oblastí, kam se budou data sdružovat
n_components = 8
samples, labels = make_blobs(
n_samples=n_samples, n_features=3, centers=n_components,
cluster_std=0.80, random_state=0
)
# příprava 3D grafu
fig = plt.figure(figsize=(6.4, 6.4))
ax = fig.add_subplot(projection="3d")
# vykreslení grafu
ax.scatter(samples[:,0], samples[:,1], samples[:,2], marker=".", s=1)
# uložení grafu do souboru
plt.savefig("blobs_3D.png")
# zobrazení grafu
plt.show()
Výsledkem činnosti tohoto skriptu bude graf s celkem 10000 body:
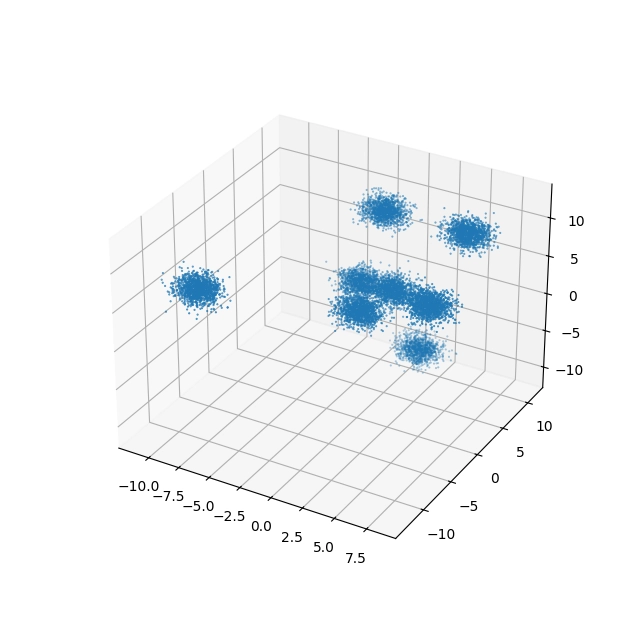
Obrázek 5: 10000 bodů, které se seskupují okolo osmi center.
7. Zvětšení směrodatné odchylky při generování bodů v 3D prostoru
Modifikací nepovinného parametru cluster_std předaného do funkce sklearn.datasets.make_blobs se specifikuje hodnota směrodatné odchylky využité při generování bodů v prostoru. Čím menší je tato hodnota, tím více se budou výsledné body přibližovat svému centrálnímu bodu a naopak. Pokud tedy hodnotu směrodatné odchylky zvětšíme, budou body rozmístěny v prostoru dále od centrálních bodů a oblasti centrálních bodů se mohou začít překrývat (což přesně potřebujeme, abychom mohli odhadnout kvality algoritmů pro shlukovou analýzu). Pokusme se tedy směrodatnou odchylku nastavit na hodnotu 1,8:
#!/usr/bin/env python
# Vykreslení bodů v 3D prostoru
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
# celkový počet vypočtených bodů
n_samples = 10000
# počet oblastí, kam se budou data sdružovat
n_components = 8
samples, labels = make_blobs(
n_samples=n_samples, n_features=3, centers=n_components,
cluster_std=1.80, random_state=0
)
# příprava 3D grafu
fig = plt.figure(figsize=(6.4, 6.4))
ax = fig.add_subplot(projection="3d")
# vykreslení grafu
ax.scatter(samples[:,0], samples[:,1], samples[:,2], marker=".", s=1)
# uložení grafu do souboru
plt.savefig("blobs_3D_spread.png")
# zobrazení grafu
plt.show()
Výsledný graf by měl vypadat následovně:
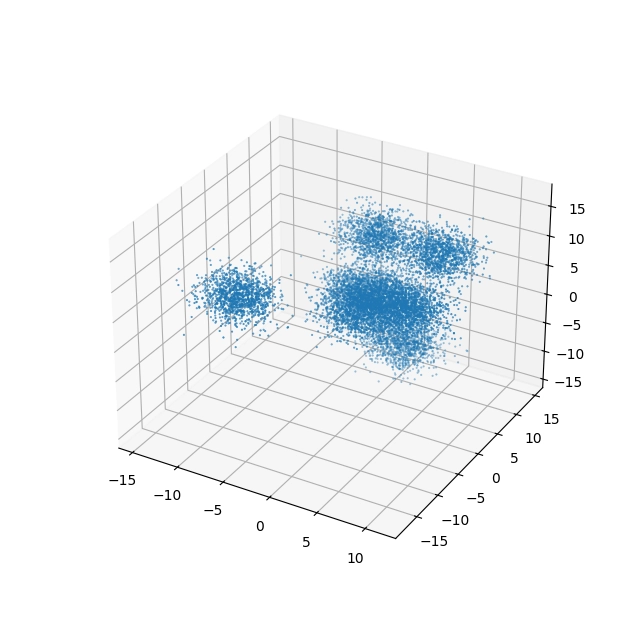
Obrázek 6: 10000 bodů, které se seskupují okolo osmi center, ovšem s větší směrodatnou odchylkou.
8. Několik různých pohledů na body v 3D prostoru
Z předchozích obrázků není zřejmé, zda body netvoří pouze shluky v rovině (přesněji řečeno v několika rovinách), protože je zobrazen pohled na ně pouze z jediného místa. Ovšem knihovna Matplotlib umožňuje natočení celého 3D grafu, což nám umožní nechat si vytvořit několik obrázků, typicky s nárysem, půdorysem a bokorysem. Natočení se specifikuje metodou mpl_toolkits.mplot3d.axes3d.Axes3D.view_init, které se předává dvojice úhlů elevation, azimuth a roll. Posledním úhlem se specifikuje natočení kamery podle osy objektivu, takže tento úhel ponecháme na nule.
Hodnoty prvních dvou úhlů mohou být jakékoli, ovšem pro zobrazení tak, aby byla s rovinou obrázku rovnoběžná některá rovina tvořená osami, se používají pouze násobky 90° (tím zajistíme zobrazení nárysu, půdorysu, bokorysu a jejich zrcadlových protějšků – alternativně lze navíc vypnout 3D projekci):
| Rovina rovnoběžná s obrázkem | Elevation | Azimuth |
|---|---|---|
| XY | 90° | –90° |
| XZ | 0° | –90° |
| YZ | 0° | 0° |
| -XY | –90° | 90° |
| -XZ | 0° | 90° |
| -YZ | 0° | 180° |
Prakticky bude celý postup vypadat následovně. Nejdříve vytvoříme kontejner pro graf a vložíme do něj graf (s případným povolením 3D projekce):
fig = plt.figure(figsize=(6.4, 6.4)) ax = fig.add_subplot(projection="3d")
Dále lze před či po vykreslení bodů specifikovat způsob pohledu na graf:
ax.view_init(elevation, azimuth, roll)
9. Zobrazení skupiny 3D bodů ze tří směrů
Modifikace příkladu, který v prostoru pseudonáhodně rozmístí 10000 bodů a posléze je zobrazí ze tří směrů (nárys, půdorys, bokorys, ovšem stále s nastavenou 3D projekcí) může vypadat následovně:
#!/usr/bin/env python
# Vykreslení bodů v 3D prostoru
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
# celkový počet vypočtených bodů
n_samples = 10000
# počet oblastí, kam se budou data sdružovat
n_components = 8
samples, labels = make_blobs(
n_samples=n_samples, n_features=3, centers=n_components,
cluster_std=1.20, random_state=0
)
# příprava 3D grafu
fig = plt.figure(figsize=(6.4, 6.4))
ax = fig.add_subplot(projection="3d")
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
# vykreslení grafu
ax.scatter(samples[:,0], samples[:,1], samples[:,2], marker=".", s=1)
# uložení grafu do souboru
ax.view_init(90, -90, 0)
plt.savefig("blobs_view_1.png")
ax.view_init(0, -90, 0)
plt.savefig("blobs_view_2.png")
ax.view_init(0, 0, 0)
plt.savefig("blobs_view_3.png")
A takto by měly vypadat výsledné obrázky získané po spuštění skriptu:
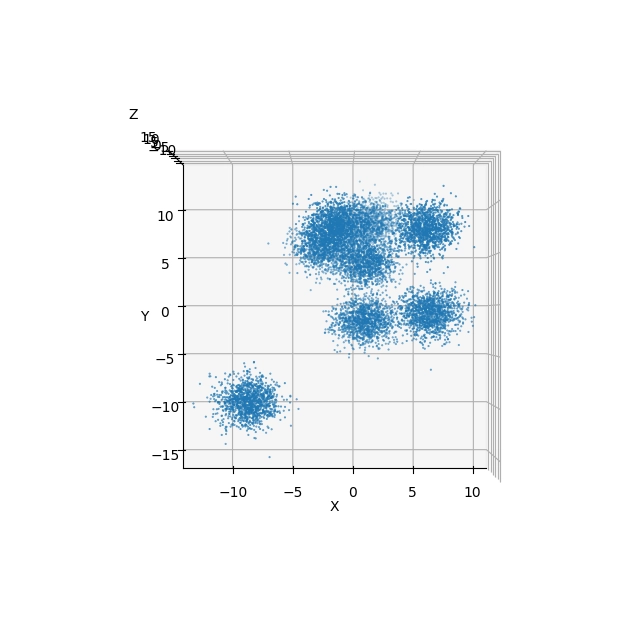
Obrázek 7: Pohled na 3D body s použitím Elevation=90° a Azimuth=-90°
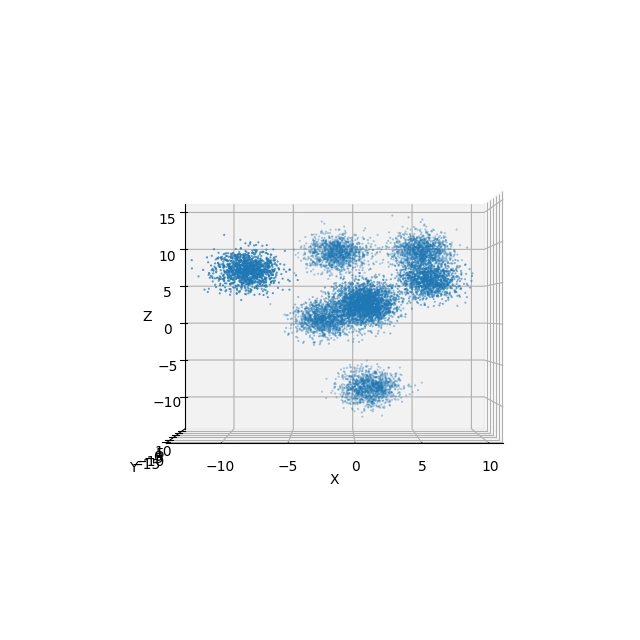
Obrázek 8: Pohled na 3D body s použitím Elevation=0° a Azimuth=-90°
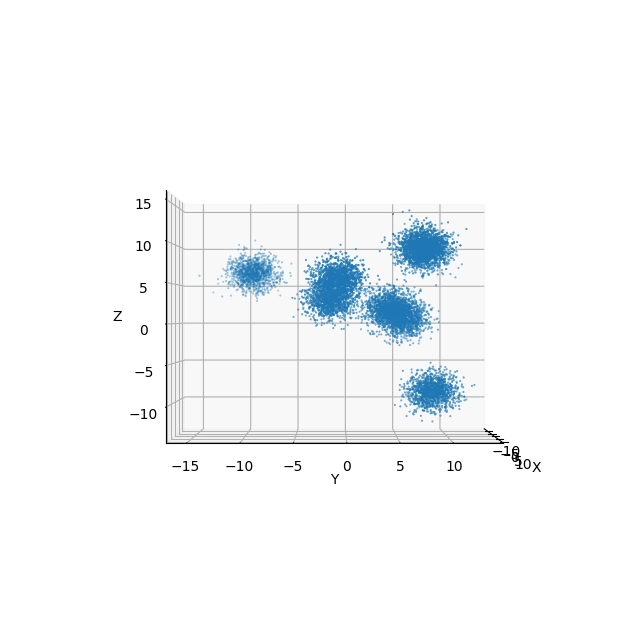
Obrázek 9: Pohled na 3D body s použitím Elevation=0° a Azimuth=0°
10. Obarvení bodů na základě toho, do jakého clusteru patří
Postup pro obarvení bodů na základě toho, do jakého clusteru patří, jsme si již popsali v úvodním článku, takže tento postup pouze rozšíříme do 3D prostoru. Připomeňme si, že funkce sklearn.datasets.make_blobs vrací nejenom souřadnice bodů (v prostoru s libovolným počtem dimenzí), ale i index (celé číslo) udávající oblast (řekněme poněkud nepřesně cluster), do které daný bod náleží. Tuto hodnotu můžeme využít ke dvěma účelům:
- Pro ověření algoritmu pro shlukovou analýzu
- Pro vizualizaci bodů, přesněji řečeno pro jejich obarvení podle oblasti
Vyzkoušejme si nyní obarvení bodů podle oblasti. Je to snadné a vlastně zcela nezávislé na tom, zda body leží v rovině nebo v prostoru. Vytvoříme si seznam (či n-tici) s osmi kódy barev, protože body jsou vytvářeny v osmi oblastech:
colors = ["#4444cc", "#44bb44", "#cc4444", "#cccc44", "#44cccc", "#cc44cc", "#cccccc", "#000000"]
Dále budeme iterovat přes prvky této kolekce a vykreslíme pouze ty body, které mají shodnou hodnotu label s indexem barvy (0–7):
for i, color in enumerate(colors):
...
...
...
Jak se vlastně provádí výběr bodů z dvourozměrného pole? Nejprve si vytvoříme pomocný vektor obsahující pouze 0 a 1, kde 1 znamená, že se má příslušný bod vybrat. Tento vektor bude použit jako selektor do původního dvourozměrného pole se souřadnicemi:
for i, color in enumerate(colors):
selector = labels == i
Nyní již stačí provést výběr z původního 3D pole s množinou bodů a následně pouze vybrané body vykreslit:
ax.scatter(samples[selector,0], samples[selector,1], samples[selector,2], marker=".", s=1)
Celý skript bude vypadat následovně:
#!/usr/bin/env python
# Vykreslení bodů v 3D prostoru
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
# celkový počet vypočtených bodů
n_samples = 10000
# počet oblastí, kam se budou data sdružovat
n_components = 8
samples, labels = make_blobs(
n_samples=n_samples, n_features=3, centers=n_components,
cluster_std=0.80, random_state=0
)
# barvy použité pro obarvení bodů
colors = ["#4444cc", "#44bb44", "#cc4444", "#cccc44", "#44cccc", "#cc44cc", "#cccccc", "#000000"]
# příprava 3D grafu
fig = plt.figure(figsize=(6.4, 6.4))
ax = fig.add_subplot(projection="3d")
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
# vykreslení grafu
for i, color in enumerate(colors):
selector = labels == i
ax.scatter(samples[selector,0], samples[selector,1], samples[selector,2], marker=".", s=1)
# uložení grafu do souboru
plt.savefig("colorized_blobs_3D.png")
# uložení grafu do souboru
ax.view_init(90, -90, 0)
plt.savefig("colorized_blobs_view_1.png")
ax.view_init(0, -90, 0)
plt.savefig("colorized_blobs_view_2.png")
ax.view_init(0, 0, 0)
plt.savefig("colorized_blobs_view_3.png")
Získané výsledky ukazují, že náš postup je korektní:
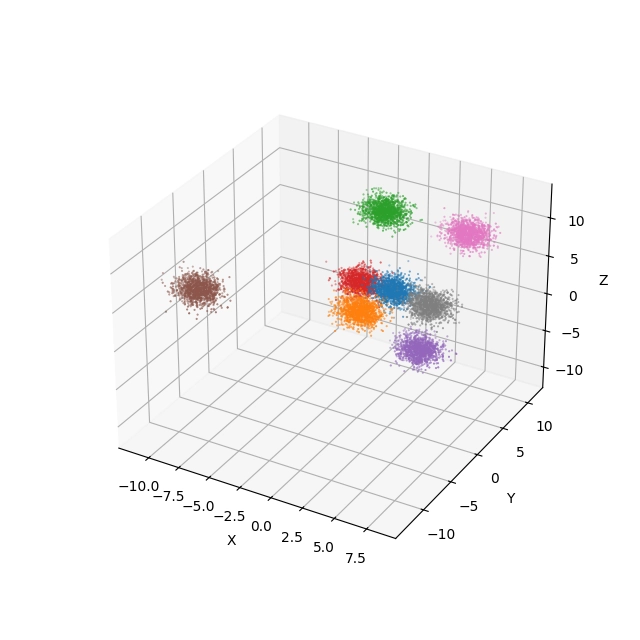
Obrázek 10: 3D projekce a pohled na obarvené body.
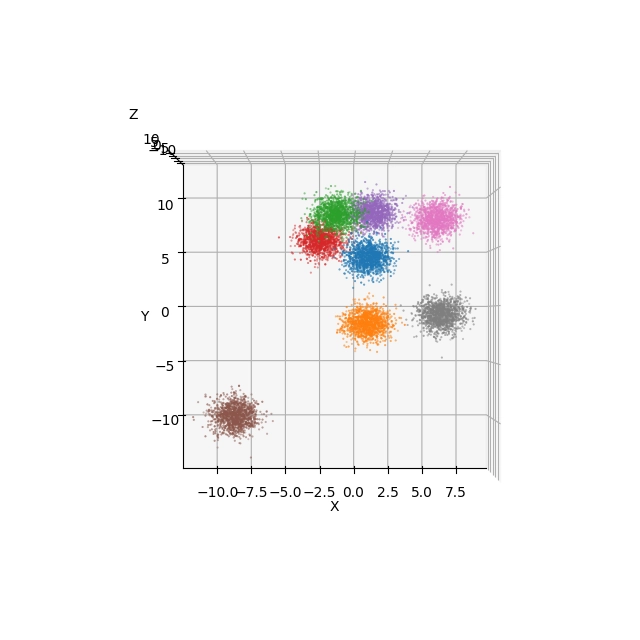
Obrázek 11: Pohled na obarvené 3D body s použitím Elevation=90° a Azimuth=-90°
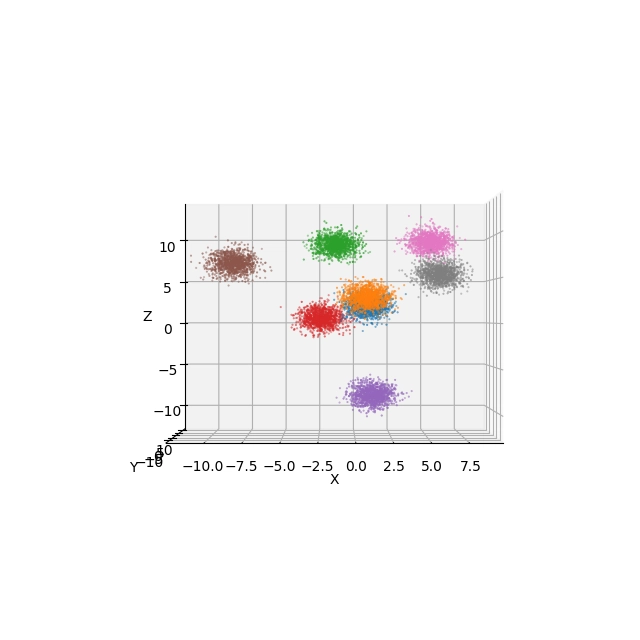
Obrázek 12: Pohled na obarvené 3D body s použitím Elevation=0° a Azimuth=-90°
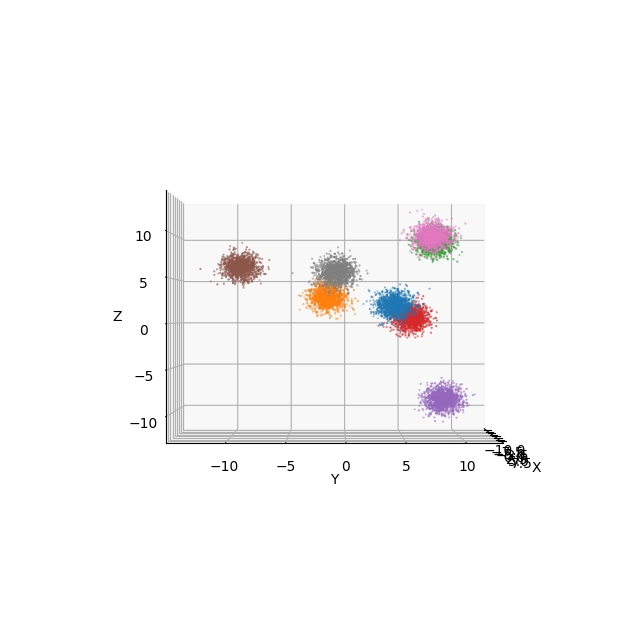
Obrázek 13: Pohled na obarvené 3D body s použitím Elevation=0° a Azimuth=0°
11. Nalezení centroidů a provedení shlukové analýzy algoritmem K-means
Následuje nejdůležitější krok – vlastní provedení shlukové analýzy. Použijeme přitom opět algoritmus K-means, který není omezen pouze na 2D rovinu. Je tomu tak proto, že tento algoritmus je založen na předpokladu, že vstupní objekty jsou chápány jako skutečné body v nějakém eukleidovském prostoru a již dopředu víme, kolik shluků (clusterů) má existovat. A eukleidovský prostor může být i trojrozměrný (resp. n-rozměrný). Algoritmus K-means nejprve nalezne takzvané centroidy a následně jsou vstupní objekty (body) zařazeny k tomu centroidu, který je k bodu nejblíže. Poté se provádí další iterace; centroidy se přesunou do těžiště clusteru a provede se nové přiřazení.
Díky tomu, že již algoritmus K-means dobře známe, můžeme bez dalšího podrobnějšího popisu přistoupit k jeho použití. Oproti příkladům z předchozích dvou článků pouze nesmíme zapomenout na správné vyplnění parametru n_clusters, protože budeme hledat osm centroidů:
#!/usr/bin/env python
# Vykreslení bodů v 3D prostoru
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
# celkový počet vypočtených bodů
n_samples = 10000
# počet oblastí, kam se budou data sdružovat
n_components = 8
samples, _ = make_blobs(
n_samples=n_samples, n_features=3, centers=n_components,
cluster_std=0.80, random_state=0
)
# barvy použité pro obarvení bodů
colors = ["#4444cc", "#44bb44", "#cc4444", "#cccc44", "#44cccc", "#cc44cc", "#cccccc", "#000000"]
# příprava 3D grafu
fig = plt.figure(figsize=(6.4, 6.4))
ax = fig.add_subplot(projection="3d")
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
# clustering
kmeans = KMeans(n_clusters=n_components, random_state=0, n_init="auto").fit(samples)
# vykreslit centra nalezených oblastí
ax.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], kmeans.cluster_centers_[:, 2], c="red", s=50)
# vykreslení bodů s jejich přiřazením ke clusteru
for i, color in enumerate(colors):
selector = kmeans.labels_ == i
ax.scatter(samples[selector,0], samples[selector,1], samples[selector,2], marker=".", s=1)
# uložení grafu do souboru
plt.savefig("kmeans_blobs_3D.png")
# uložení grafu do souboru
ax.view_init(90, -90, 0)
plt.savefig("kmeans_blobs_view_1.png")
ax.view_init(0, -90, 0)
plt.savefig("kmeans_blobs_view_2.png")
ax.view_init(0, 0, 0)
plt.savefig("kmeans_blobs_view_3.png")
Opět se samozřejmě podívejme na výsledky získané shlukovou analýzou:
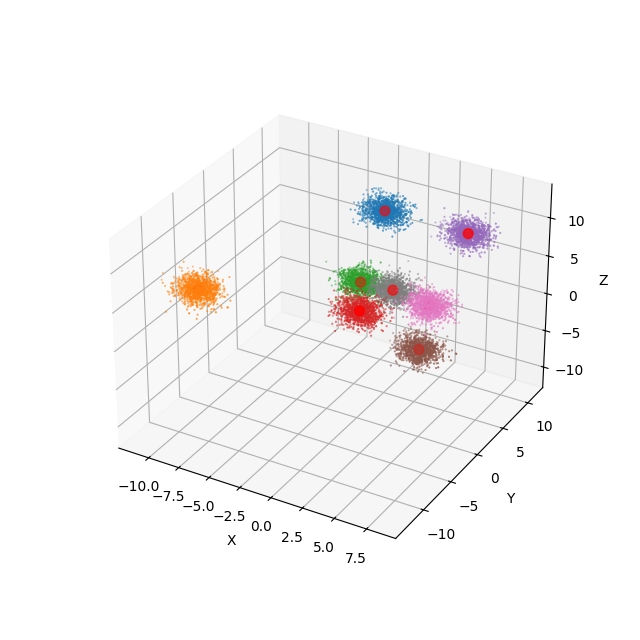
Obrázek 14: 3D projekce a pohled na výsledek shlukové analýzy
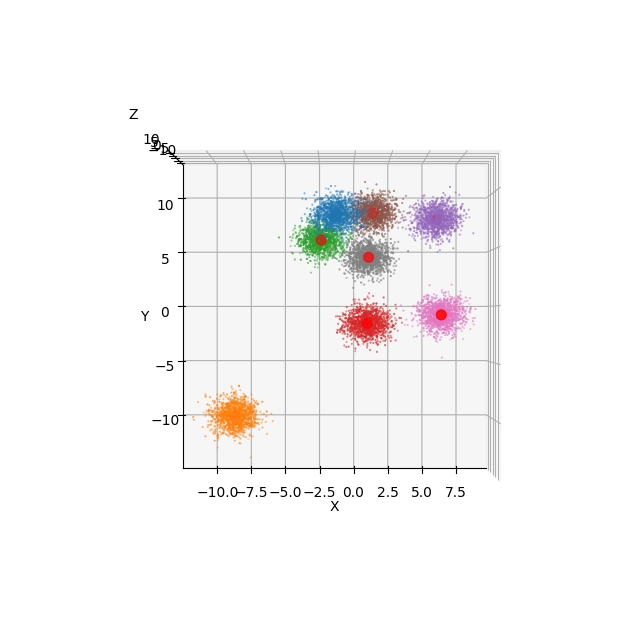
Obrázek 15: Pohled na výsledek shlukové analýzy s použitím Elevation=90° a Azimuth=-90°
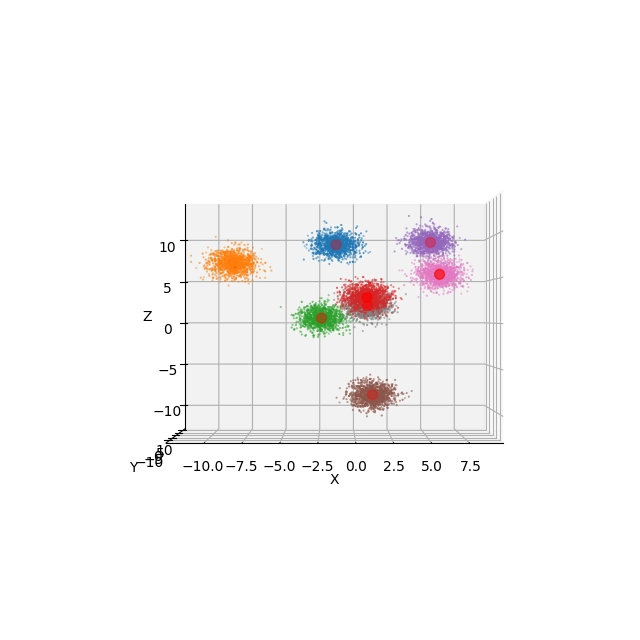
Obrázek 16: Pohled na výsledek shlukové analýzy s použitím Elevation=0° a Azimuth=-90°
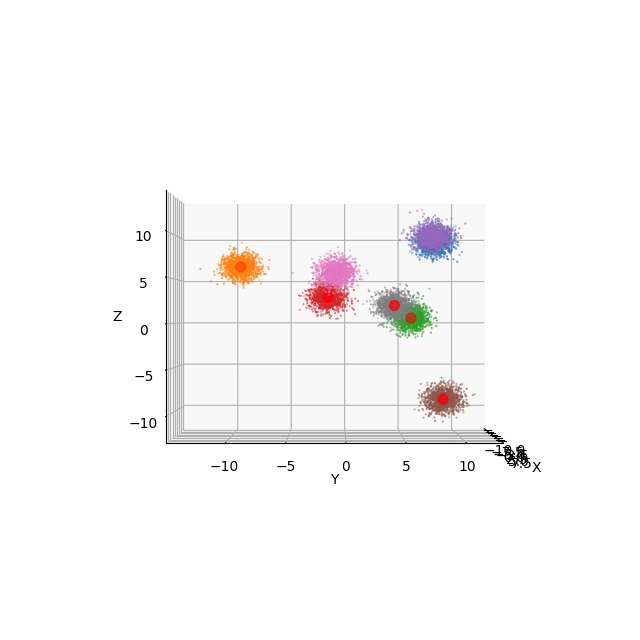
Obrázek 17: Pohled na výsledek shlukové analýzy s použitím Elevation=0° a Azimuth=0°
12. Algoritmus K-means a náhodněji rozmístěné body v prostoru
Z příkladů v 2D jsme se dozvěděli, že pokud jsou body v rovině rozmístěny náhodněji (a navíc pokud se budou oblasti centroidů překrývat), začne výsledek připomínat Voronoiův diagram:

Obrázek 18: Výsledek clusteringu pro překrývající se oblasti centroidů.
Jak tomu bude v 3D prostoru? Můžeme si to vyzkoušet tak, že budeme postupně zvětšovat směrodatnou odchylku (viz sedmou kapitolu):
#!/usr/bin/env python
# Vykreslení bodů v 3D prostoru
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
# celkový počet vypočtených bodů
n_samples = 10000
# počet oblastí, kam se budou data sdružovat
n_components = 8
samples, _ = make_blobs(
n_samples=n_samples, n_features=3, centers=n_components,
cluster_std=1.80, random_state=0
)
# barvy použité pro obarvení bodů
colors = ["#4444cc", "#44bb44", "#cc4444", "#cccc44", "#44cccc", "#cc44cc", "#cccccc", "#000000"]
# příprava 3D grafu
fig = plt.figure(figsize=(6.4, 6.4))
ax = fig.add_subplot(projection="3d")
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
# clustering
kmeans = KMeans(n_clusters=n_components, random_state=0, n_init="auto").fit(samples)
# vykreslit centra nalezených oblastí
ax.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], kmeans.cluster_centers_[:, 2], c="red", s=50)
# vykreslení bodů s jejich přiřazením ke clusteru
for i, color in enumerate(colors):
selector = kmeans.labels_ == i
ax.scatter(samples[selector,0], samples[selector,1], samples[selector,2], marker=".", s=1)
# uložení grafu do souboru
plt.savefig("kmeans_spread_blobs_3D.png")
# uložení grafu do souboru
ax.view_init(90, -90, 0)
plt.savefig("kmeans_spread_blobs_view_1.png")
ax.view_init(0, -90, 0)
plt.savefig("kmeans_spread_blobs_view_2.png")
ax.view_init(0, 0, 0)
plt.savefig("kmeans_spread_blobs_view_3.png")
Výsledky:
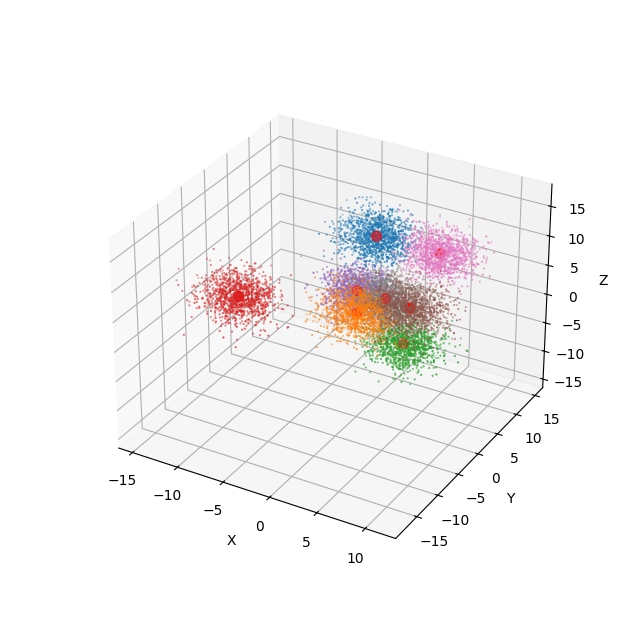
Obrázek 19: 3D projekce a pohled na výsledek shlukové analýzy
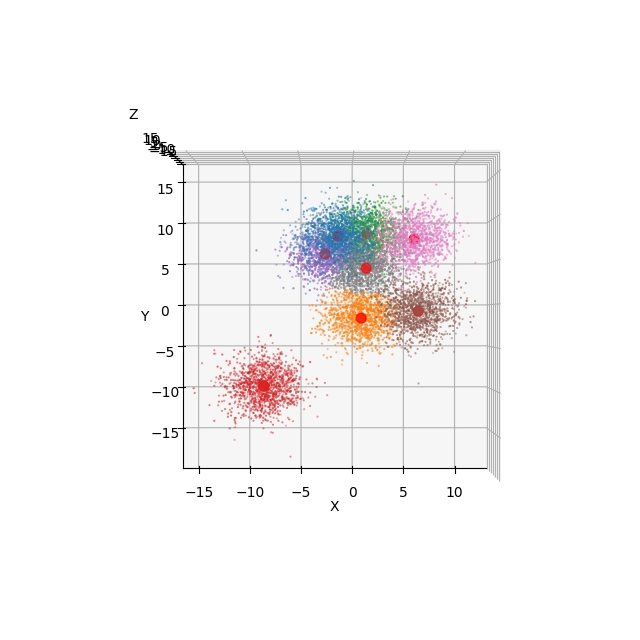
Obrázek 20: Pohled na výsledek shlukové analýzy s použitím Elevation=90° a Azimuth=-90°
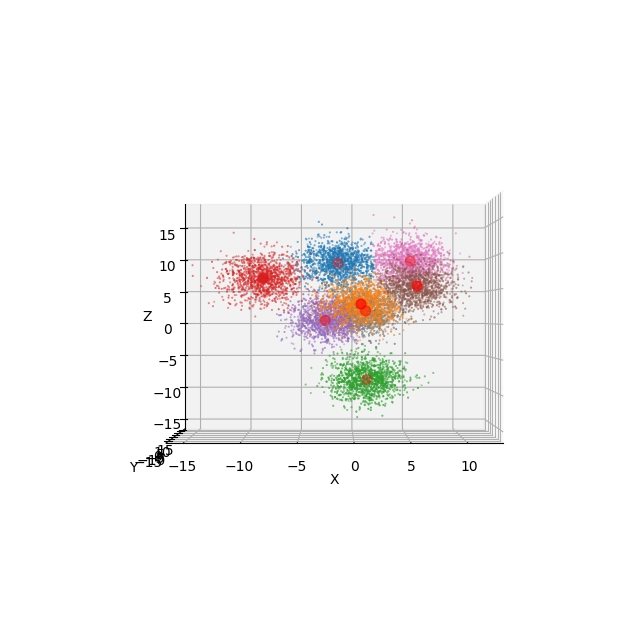
Obrázek 21: Pohled na výsledek shlukové analýzy s použitím Elevation=0° a Azimuth=-90°
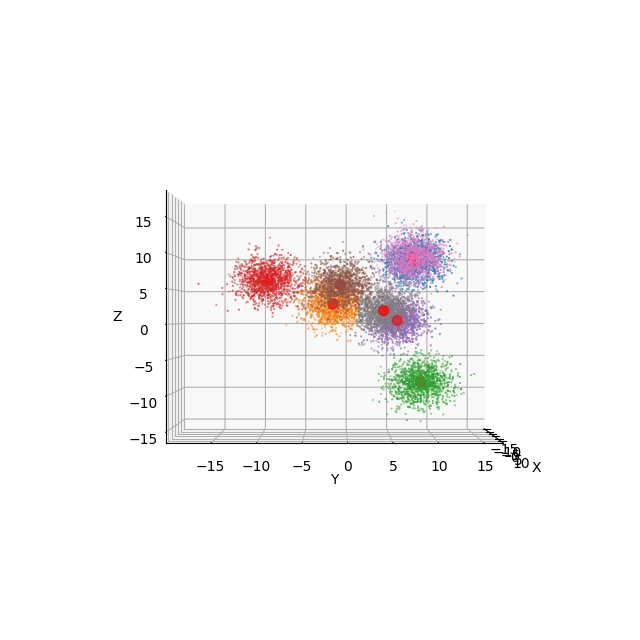
Obrázek 22: Pohled na výsledek shlukové analýzy s použitím Elevation=0° a Azimuth=0°
Ještě více náhodné rozmístění bodů společně se zvýšením jejich počtu:
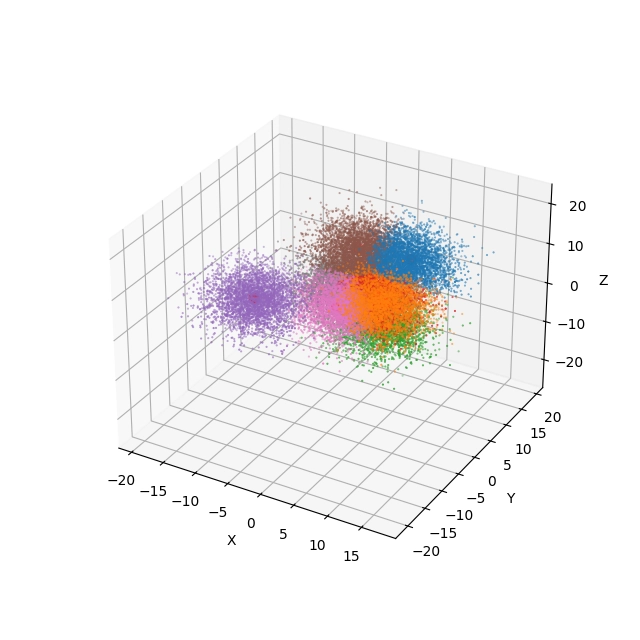
Obrázek 23: 3D projekce a pohled na výsledek shlukové analýzy
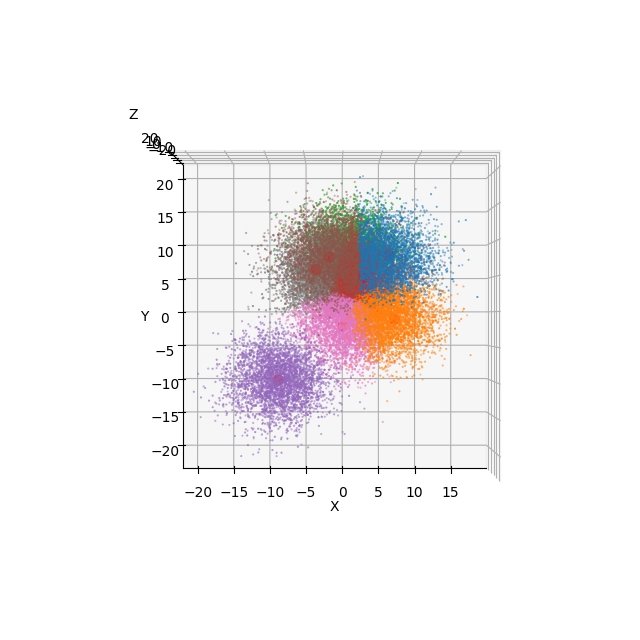
Obrázek 24: Pohled na výsledek shlukové analýzy s použitím Elevation=90° a Azimuth=-90°
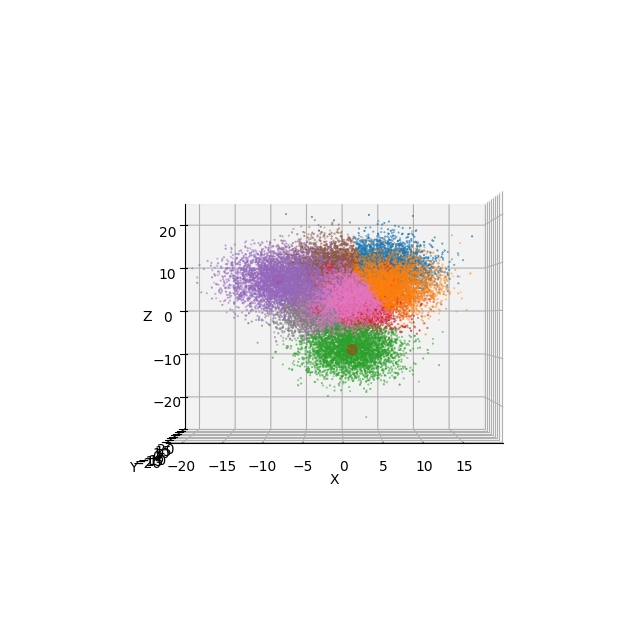
Obrázek 25: Pohled na výsledek shlukové analýzy s použitím Elevation=0° a Azimuth=-90°
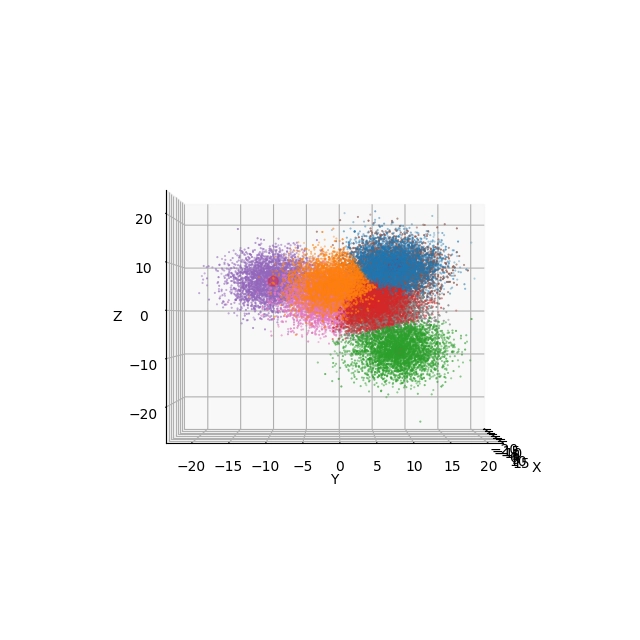
Obrázek 26: Pohled na výsledek shlukové analýzy s použitím Elevation=0° a Azimuth=0°
13. Algoritmus K-means a zcela náhodně rozmístěné body v prostoru
Zajímavé bude zjistit, jak algoritmus K-means rozdělí oblast, v níž budou body rozmístěny zcela náhodně. Budeme přitom chtít detekovat osm oblastí. Proč právě osm bude patrné při pohledu na obrázky s obarvenými body, které tímto způsobem získáme:
#!/usr/bin/env python
# Vykreslení bodů v 3D prostoru
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans
# počet oblastí, kam se budou data sdružovat
n_components = 8
# počet vygenerovaných bodů
n_samples = 50000
samples = np.random.rand(n_samples, 3)
# barvy použité pro obarvení bodů
colors = ["#4444cc", "#44bb44", "#cc4444", "#cccc44", "#44cccc", "#cc44cc", "#cccccc", "#000000"]
# příprava 3D grafu
fig = plt.figure(figsize=(6.4, 6.4))
ax = fig.add_subplot(projection="3d")
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
# clustering
kmeans = KMeans(n_clusters=n_components, random_state=0, n_init="auto").fit(samples)
# vykreslit centra nalezených oblastí
ax.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], kmeans.cluster_centers_[:, 2], c="red", s=50)
# vykreslení bodů s jejich přiřazením ke clusteru
for i, color in enumerate(colors):
selector = kmeans.labels_ == i
ax.scatter(samples[selector,0], samples[selector,1], samples[selector,2], marker=".", s=1)
# uložení grafu do souboru
plt.savefig("kmeans_spread_random_3D.png")
# uložení grafu do souboru
ax.view_init(90, -90, 0)
plt.savefig("kmeans_spread_random_view_1.png")
ax.view_init(0, -90, 0)
plt.savefig("kmeans_spread_random_view_2.png")
ax.view_init(0, 0, 0)
plt.savefig("kmeans_spread_random_view_3.png")
Ze zobrazených výsledků je patrné, že centroidy byly nalezeny ve středech osmi pomyslných krychlí, které celý prostor rozdělí na osm prakticky shodných oblastí:
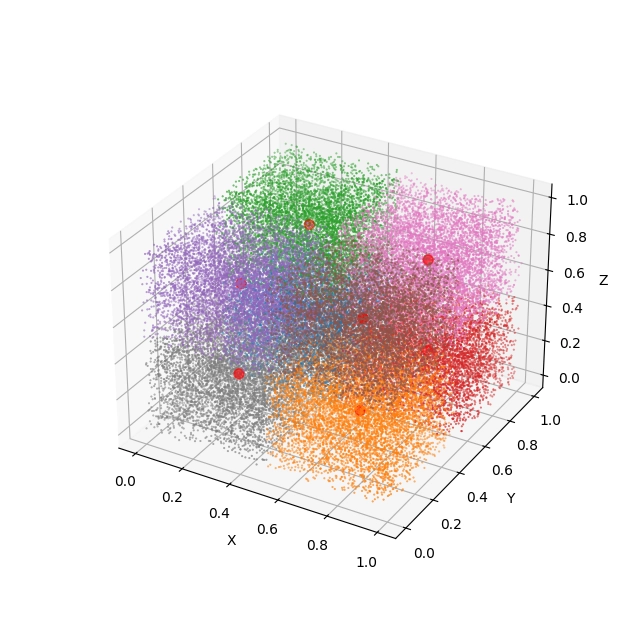
Obrázek 27: 3D projekce a pohled na výsledek shlukové analýzy
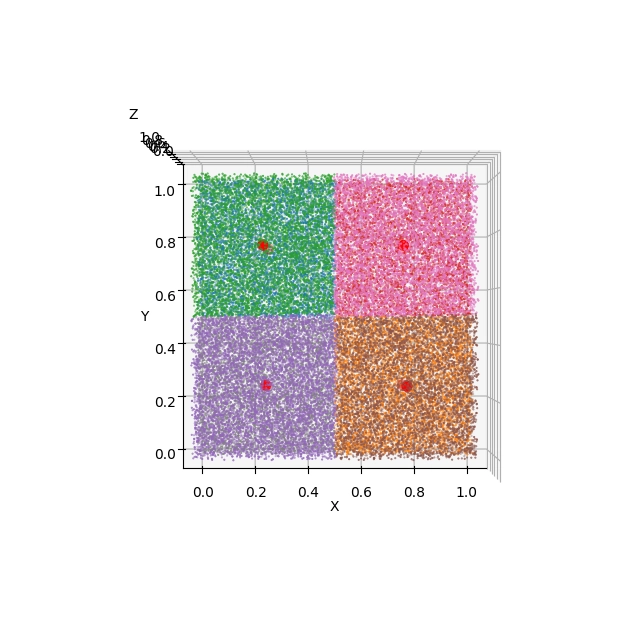
Obrázek 28: Pohled na výsledek shlukové analýzy s použitím Elevation=90° a Azimuth=-90°
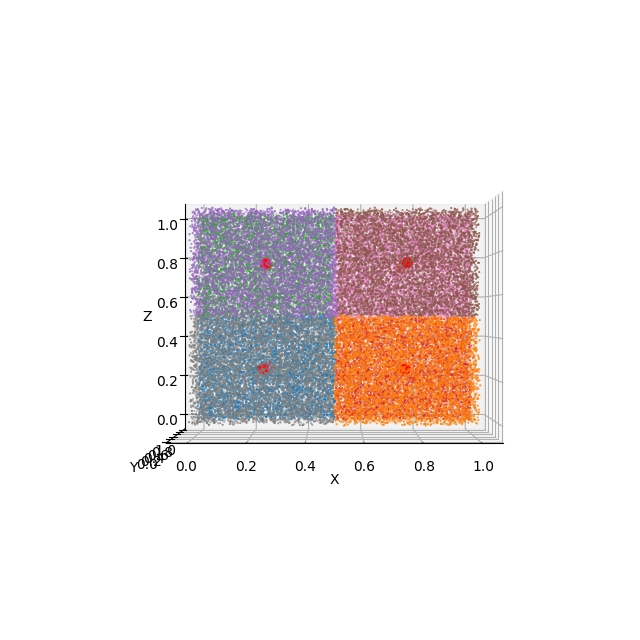
Obrázek 29: Pohled na výsledek shlukové analýzy s použitím Elevation=0° a Azimuth=-90°
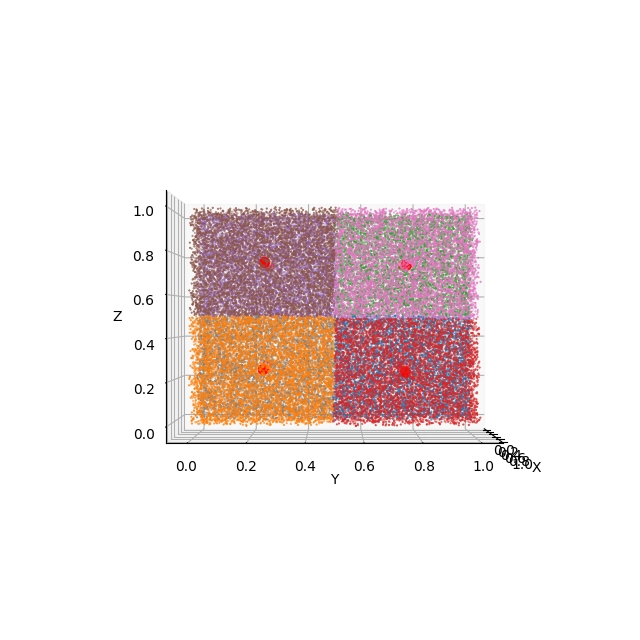
Obrázek 30: Pohled na výsledek shlukové analýzy s použitím Elevation=0° a Azimuth=0°
14. Časová náročnost algoritmu K-means
Časová složitost algoritmu K-means je pochopitelně závislá na počtu bodů, které se mají rozdělit do oblastí shlukovou analýzou. Ovšem bude závislá i na náhodnosti či naopak nějaké regularitě v rozmístění bodů? To se pokusíme zjistit s využitím tří benchmarků, které budou provádět tato měření:
- Benchmark pro postupně rostoucí počet bodů tvořících shluky
- Benchmark pro postupně rostoucí počet bodů rozmístěných náhodně
- Benchmark pro stále stejný počet bodů, u jejichž rozmístění v prostoru se používá stále větší směrodatná odchylka
15. Zdrojové kódy benchmarků
#!/usr/bin/env python
from time import perf_counter
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
def run_k_means(n_samples):
# počet oblastí, kam se budou data sdružovat
n_components = 8
samples, _ = make_blobs(
n_samples=n_samples, n_features=3, centers=n_components,
cluster_std=0.80, random_state=0
)
# clustering
kmeans = KMeans(n_clusters=n_components, random_state=0, n_init="auto").fit(samples)
x = []
y = []
for i in range(10000, 1000000, 10000):
started = perf_counter()
run_k_means(i)
finished = perf_counter()
duration = finished - started
x.append(i)
y.append(duration)
print(i, duration)
plt.figure(1)
plt.plot(x, y, marker="o")
plt.savefig("benchmark1.png")
plt.show()
#!/usr/bin/env python
from time import perf_counter
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans
def run_k_means(n_samples):
# počet oblastí, kam se budou data sdružovat
n_components = 8
samples = np.random.rand(n_samples, 3)
# clustering
kmeans = KMeans(n_clusters=n_components, random_state=0, n_init="auto").fit(samples)
x = []
y = []
for i in range(10000, 1000000, 10000):
started = perf_counter()
run_k_means(i)
finished = perf_counter()
duration = finished - started
x.append(i)
y.append(duration)
print(i, duration)
plt.figure(1)
plt.plot(x, y, marker="o")
plt.savefig("benchmark3.png")
plt.show()
#!/usr/bin/env python
from time import perf_counter
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
def run_k_means(n_samples, std):
# počet oblastí, kam se budou data sdružovat
n_components = 8
samples, _ = make_blobs(
n_samples=n_samples, n_features=3, centers=n_components,
cluster_std=std, random_state=0
)
# clustering
kmeans = KMeans(n_clusters=n_components, random_state=0, n_init="auto").fit(samples)
x = []
y = []
for i in range(0, 100):
std = i / 10.0
started = perf_counter()
run_k_means(20000, std)
finished = perf_counter()
duration = finished - started
x.append(std)
y.append(duration)
print(std, duration)
plt.figure(1)
plt.plot(x, y, marker="o")
plt.savefig("benchmark4.png")
plt.show()
16. Zobrazení vlivu počtu bodů na rychlost algoritmu K-means
Předností standardně implementovaného algoritmu K-means je fakt, že je jeho časová složitost pouze lineární a závislá jak na počtu centroidů, tak na počtu vstupních bodů. Ovšem pozor: to platí pro algoritmus s pevným počtem iterací, protože jeho „ideální“ podoba, která vrací ideální rozdělení bodů, je NP-složitá!:
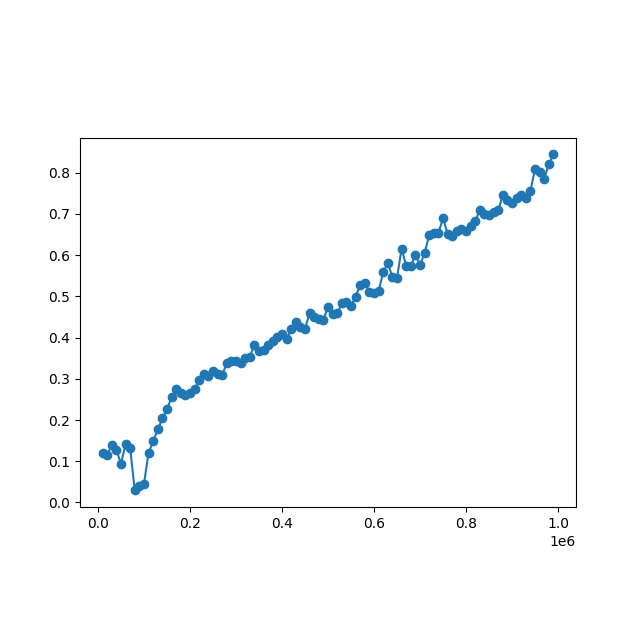
Obrázek 31: Benchmark pro postupně rostoucí počet bodů tvořících shluky.
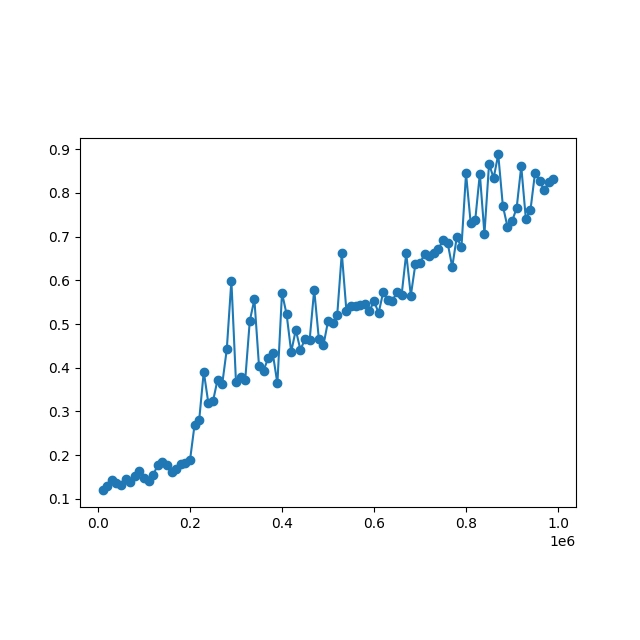
Obrázek 32: Benchmark pro postupně rostoucí počet bodů tvořících shluky s větší směrodatnou odchylkou.
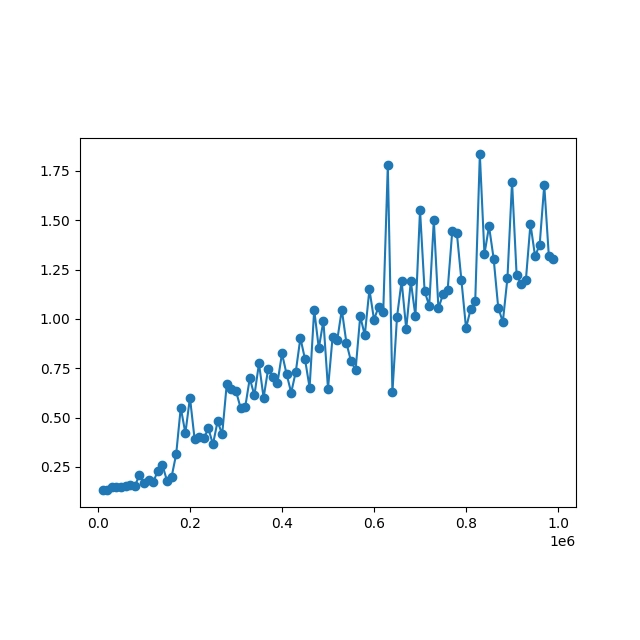
Obrázek 33: Benchmark pro postupně rostoucí počet bodů rozmístěných náhodně.
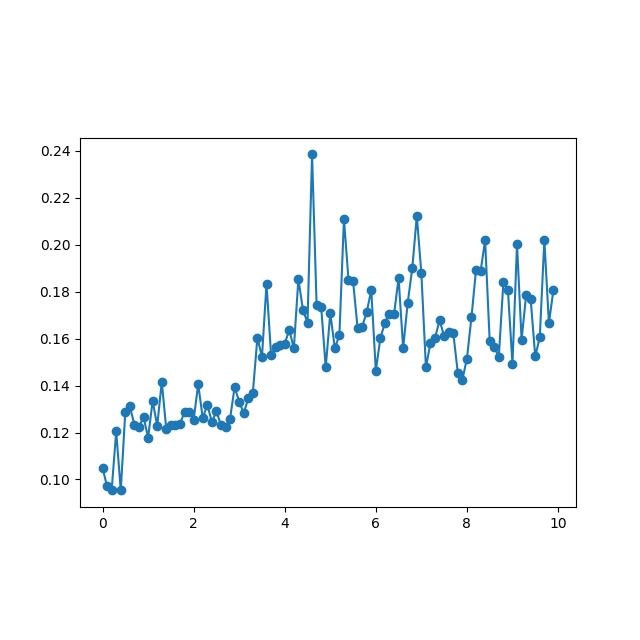
Obrázek 34: Benchmark pro stále stejný počet bodů, u jejichž rozmístění v prostoru se používá stále větší směrodatná odchylka.
17. Repositář s demonstračními příklady
Všechny demonstrační příklady využívající knihovnu Scikit-learn lze nalézt v repositáři https://github.com/tisnik/most-popular-python-libs. Následují odkazy na jednotlivé příklady i na (Jupyter) diáře s postupem výpočtů a analýz:
18. Odkazy na Internetu
- scikit-learn: Machine Learning in Python
https://scikit-learn.org/stable/index.html - Sklearn-pandas
https://github.com/scikit-learn-contrib/sklearn-pandas - sklearn-xarray
https://github.com/phausamann/sklearn-xarray/ - Clustering
https://scikit-learn.org/stable/modules/clustering.html - Cluster analysis (Wikipedia)
https://en.wikipedia.org/wiki/Cluster_analysis - Shluková analýza (Wikipedia)
https://cs.wikipedia.org/wiki/Shlukov%C3%A1_anal%C3%BDza - K-means
https://cs.wikipedia.org/wiki/K-means - k-means clustering
https://en.wikipedia.org/wiki/K-means_clustering - Spectral clustering
https://en.wikipedia.org/wiki/Spectral_clustering - Emergence
https://cs.wikipedia.org/wiki/Emergence - Particle Life: Vivid structures from rudimentary rules
https://particle-life.com/ - Hertzsprungův–Russellův diagram
https://cs.wikipedia.org/wiki/Hertzsprung%C5%AFv%E2%80%93Russell%C5%AFv_diagram - Using Machine Learning in an HR Diagram
https://cocalc.com/share/public_paths/08b6e03583cbdef3cdb9813a54ec68ff773c747f - Gaia H-R diagrams: Querying Gaia data for one million nearby stars
https://vlas.dev/post/gaia-dr2-hrd/ - The Hertzsprung–Russell diagram
https://scipython.com/book2/chapter-9-data-analysis-with-pandas/problems/p92/the-hertzsprung-russell-diagram/ - Animated Hertzsprung-Russell Diagram with 119,614 datapoints
https://github.com/zonination/h-r-diagram - Neuraxle Pipelines
https://github.com/Neuraxio/Neuraxle - scikit-learn: Getting Started
https://scikit-learn.org/stable/getting_started.html - Support Vector Machines
https://scikit-learn.org/stable/modules/svm.html - Use Deep Learning to Detect Programming Languages
http://searene.me/2017/11/26/use-neural-networks-to-detect-programming-languages/ - Natural-language processing
https://en.wikipedia.org/wiki/Natural-language_processing - THE MNIST DATABASE of handwritten digits
http://yann.lecun.com/exdb/mnist/ - MNIST database (Wikipedia)
https://en.wikipedia.org/wiki/MNIST_database - MNIST For ML Beginners
https://www.tensorflow.org/get_started/mnist/beginners - Stránka projektu Torch
http://torch.ch/ - Torch: Serialization
https://github.com/torch/torch7/blob/master/doc/serialization.md - Torch: modul image
https://github.com/torch/image/blob/master/README.md - Data pro neuronové sítě
http://archive.ics.uci.edu/ml/index.php - Torch na GitHubu (několik repositářů)
https://github.com/torch - Torch (machine learning), Wikipedia
https://en.wikipedia.org/wiki/Torch_%28machine_learning%29 - Torch Package Reference Manual
https://github.com/torch/torch7/blob/master/README.md - Torch Cheatsheet
https://github.com/torch/torch7/wiki/Cheatsheet - Neural network containres (Torch)
https://github.com/torch/nn/blob/master/doc/containers.md - Simple layers
https://github.com/torch/nn/blob/master/doc/simple.md#nn.Linear - Transfer Function Layers
https://github.com/torch/nn/blob/master/doc/transfer.md#nn.transfer.dok - Feedforward neural network
https://en.wikipedia.org/wiki/Feedforward_neural_network - Biologické algoritmy (4) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-4-neuronove-site/ - Biologické algoritmy (5) – Neuronové sítě
https://www.root.cz/clanky/biologicke-algoritmy-5-neuronove-site/ - Umělá neuronová síť (Wikipedia)
https://cs.wikipedia.org/wiki/Um%C4%9Bl%C3%A1_neuronov%C3%A1_s%C3%AD%C5%A5 - PyTorch
http://pytorch.org/ - JupyterLite na PyPi
https://pypi.org/project/jupyterlite/ - JupyterLite na GitHubu
https://github.com/jupyterlite/jupyterlite - Dokumentace k projektu JupyterLite
https://github.com/jupyterlite/jupyterlite - Matplotlib Home Page
http://matplotlib.org/ - Matplotlib (Wikipedia)
https://en.wikipedia.org/wiki/Matplotlib - Popis barvových map modulu matplotlib.cm
https://gist.github.com/endolith/2719900#id7 - Ukázky (palety) barvových map modulu matplotlib.cm
http://matplotlib.org/examples/color/colormaps_reference.html - Galerie grafů vytvořených v Matplotlibu
https://matplotlib.org/3.2.1/gallery/ - 3D rendering
https://en.wikipedia.org/wiki/3D_rendering - 3D computer graphics
https://en.wikipedia.org/wiki/3D_computer_graphics - Primary 3D view planes
https://matplotlib.org/stable/gallery/mplot3d/view_planes_3d.html




































