Obsah
2. Reálné kořeny kvadratické rovnice
3. Komplexní kořeny kvadratické rovnice
4. Hledání kořenů kubické rovnice
5. Kořeny polynomů vyšších stupňů
6. Průchod nulovými body periodické funkce
7. Vyhledání všech možných řešení
8. Vyhledání řešení pro funkci sinc
9. Řešení jednoduché nerovnice
10. Vyřešení složitější nerovnice
11. Vyřešení soustavy nerovnic
12. Složitější soustava nerovnic
13. Knihovna SymPy a Jupyter Notebook
14. Instalace Jupyter Notebooku
15. Nastavení Jupyter Notebooku
16. Ukázky použití knihovny SymPy v Jupyter Notebooku
17. Vykreslení grafů knihovnou SymPy
19. Repositář s demonstračními příklady
1. Symboly vs. proměnné
Na úvodní článek o knihovně SymPy dnes navážeme. Ukážeme si některé její další vlastnosti a popíšeme si podrobněji, jak jednotlivé funkce (provádějící manipulace s matematickými symboly) použít.
Bez dlouhého úvodu si ukažme, jaký je rozdíl mezi symboly použitými v matematických výrazech (typicky ve výsledné tištěné podobě) a symboly/proměnnými, které jsou využity při zápisu těchto výrazů v Pythonu. Prozatím jsme totiž pro pojmenování symbolů i proměnných používali stejné znaky tak, jako je tomu například v následujícím příkladu pro řešení kvadratické rovnice:
from sympy import solve, symbols, pprint
a, b, c, x = symbols('a,b,c,x')
f = a*x**2 + b*x + c
pprint(f)
solution = solve(f, x)
pprint(solution)
Výsledkem činnosti tohoto skriptu byl následující výstup:
2 a⋅x + b⋅x + c ⎡ _____________ _____________⎤ ⎢ ╱ 2 ╱ 2 ⎥ ⎢-b - ╲╱ -4⋅a⋅c + b -b + ╲╱ -4⋅a⋅c + b ⎥ ⎢─────────────────────, ─────────────────────⎥ ⎣ 2⋅a 2⋅a ⎦
Ve skutečnosti však mohou být jména symbolů použitých v tištěné podobě odlišná od Pythonovských proměnných, což je ukázáno v dalším demonstračním příkladu. Namísto symbolů a, b a c zde používáme symboly α, β a Γ, ovšem přiřazené do proměnných s původním jménem:
from sympy import solve, symbols, pprint, init_printing
init_printing(use_unicode=True)
a, b, c, x = symbols('α,β,Γ,x')
f = a*x**2 + b*x + c
pprint(f)
solution = solve(f, x)
pprint(solution)
Výsledek bude v tomto případě odlišný, neboť se použijí námi definované symboly:
2 x ⋅α + x⋅β + Γ ⎡ _____________ _____________⎤ ⎢ ╱ 2 ╱ 2 ⎥ ⎢-β - ╲╱ -4⋅Γ⋅α + β -β + ╲╱ -4⋅Γ⋅α + β ⎥ ⎢─────────────────────, ─────────────────────⎥ ⎣ 2⋅α 2⋅α ⎦
2. Reálné kořeny kvadratické rovnice
Funkce solve, s níž jsme se v krátkosti seznámili minule, je v mnoha případech velmi užitečná, takže si v této kapitole i v kapitolách navazujících popíšeme jak její dobré vlastnosti, tak i některá omezení (která se mnohdy vyřeší použitím funkce solveset, jak uvidíme dále). Podívejme se nyní na velmi jednoduchý příklad, v němž s využitím funkce solve vypočteme kořeny kvadratické rovnice. Samotná rovnice je zapsána výrazem a solve v tomto případě předpokládá řešení pro pravou stranu (nezapsané) rovnice nastavenou na nulu. Samotné koeficienty kvadratické rovnice jsou vybrány takovým způsobem, aby měla dva různé reálné kořeny:
from sympy import solve, symbols, pprint, init_printing
init_printing(use_unicode=True)
x = symbols('x')
f = 5*x**2 + 5*x + 1
pprint(f)
solution = solve(f, x)
pprint(solution)
Tento skript po svém spuštění nejdříve vypíše původní výraz (v tomto případě polynom) a následně se v hranatých závorkách vypíšou oba nalezené kořeny výrazu (předpokládá se porovnání výrazu s nulou, tedy se jedná o kvadratickou rovnici):
2 5⋅x + 5⋅x + 1 ⎡ 1 √5 1 √5⎤ ⎢- ─ - ──, - ─ + ──⎥ ⎣ 2 10 2 10⎦
3. Komplexní kořeny kvadratické rovnice
Samozřejmě existují takové kvadratické rovnice, jejichž kořeny jsou komplexní. To je případ rovnice použité v dalším demonstračním příkladu:
from sympy import solve, symbols, pprint, init_printing
init_printing(use_unicode=True)
x = symbols('x')
f = 5*x**2 + 5*x + 5
pprint(f)
solution = solve(f, x)
pprint(solution)
Povšimněte si, že řešením jsou skutečně komplexní kořeny:
2 5⋅x + 5⋅x + 5 ⎡ 1 √3⋅ⅈ 1 √3⋅ⅈ⎤ ⎢- ─ - ────, - ─ + ────⎥ ⎣ 2 2 2 2 ⎦
Na některých terminálech nemusí být symbol pro imaginární jednotku ⅈ dobře čitelný! Popř. se v případě použití neúplného fontu zobrazí jako mezera.
4. Hledání kořenů kubické rovnice
Funkce solve je ovšem univerzálnější; nemusí se tedy používat pouze pro výpočet kořenů kvadratických rovnic. V dalším skriptu se pokusíme najít kořeny kubické rovnice. Pokud se nejedná o násobné kořeny (a to v tomto případě není pravda), měli bychom získat trojici hodnot (kořenů):
from sympy import solve, symbols, pprint, init_printing
init_printing(use_unicode=True)
x = symbols('x')
f = 5*x**3 + 5
pprint(f)
solution = solve(f, x)
pprint(solution)
Výsledkem výpočtů je v tomto případě jeden reálný kořen a dvojice kořenů komplexních (což jsou navíc komplexně sdružená čísla, což odpovídá geometrické interpretaci kořenů, které tvoří vrcholy rovnostranného trojúhelníku v komplexní rovině):
3 5⋅x + 5 ⎡ 1 √3⋅ⅈ 1 √3⋅ⅈ⎤ ⎢-1, ─ - ────, ─ + ────⎥ ⎣ 2 2 2 2 ⎦
5. Kořeny polynomů vyšších stupňů
Vyzkoušejme si nyní výpočet kořene polynomu stupně 10, tedy takových hodnot, které po dosazení do původního polynomu vrátí nulu. Měli bychom dostat deset výsledků (v případě, že se nebude jednat o násobné kořeny):
from sympy import solve, symbols, pprint, init_printing
init_printing(use_unicode=True)
x = symbols('x')
f = x**10 + 1
pprint(f)
solution = solve(f, x)
pprint(solution)
Výsledek vypadá takto (v tomto případě by asi bylo vhodné zvolit odlišný způsob zápisu komplexního čísla, nikoli tedy rozpis na reálnou a imaginární složku):
10
x + 1
⎡ ________
⎢ ╱ √5 5
⎢ ________ ________ √5⋅ ╱ ── + ─
⎢ ╱ √5 5 √5⋅ⅈ ⅈ ╱ √5 5 ⅈ √5⋅ⅈ ╲╱ 8 8
⎢-ⅈ, ⅈ, - ╱ ── + ─ - ──── + ─, ╱ ── + ─ - ─ + ────, - ───────────────
⎣ ╲╱ 8 8 4 4 ╲╱ 8 8 4 4 2
________ ________ ________
╱ √5 5 ╱ √5 5 ╱ √5 5
╱ ── + ─ ╱ ── + ─ √5⋅ ╱ ── + ─ √5⋅
╲╱ 8 8 ⅈ √5⋅ⅈ ╲╱ 8 8 ╲╱ 8 8 √5⋅ⅈ ⅈ ╲
+ ──────────── + ─ + ────, - ──────────── + ─────────────── - ──── - ─, - ────
2 4 4 2 2 4 4
________ ________ ________ ________
╱ 5 √5 ╱ 5 √5 ╱ √5 5 ╱ √5 5
╱ ─ - ── ╱ ─ - ── ╱ ── + ─ √5⋅ ╱ ── + ─ ______
╱ 8 8 ╲╱ 8 8 ╲╱ 8 8 ╲╱ 8 8 ⅈ ╱ 5 √
─────────── + ──────────── + ──────────── + ─────────────── + ─ + ⅈ⋅ ╱ ─ - ─
4 4 4 4 4 ╲╱ 8 8
________ ________ ________ ____
╱ √5 5 ╱ 5 √5 ╱ √5 5 ╱ 5
__ ________ √5⋅ ╱ ── + ─ √5⋅ ╱ ─ - ── ╱ ── + ─ ╱ ─ -
5 ╱ √5 5 ╲╱ 8 8 ╲╱ 8 8 ╲╱ 8 8 ╲╱ 8
─ ⋅ ╱ ── + ─ , - ─────────────── - ─────────────── - ──────────── + ────────
╲╱ 8 8 4 4 4 4
____ ________ ________
√5 ╱ √5 5 ╱ √5 5
── ________ ________ √5⋅ ╱ ── + ─ ╱ ── + ─ ╱
8 ⅈ ╱ 5 √5 ╱ √5 5 ╲╱ 8 8 ╲╱ 8 8 ╲╱
──── - ─ + ⅈ⋅ ╱ ─ - ── ⋅ ╱ ── + ─ , - ─────────────── - ──────────── - ───
4 ╲╱ 8 8 ╲╱ 8 8 4 4
________ ________ ________
╱ 5 √5 ╱ 5 √5 ╱ 5 √5
─ - ── √5⋅ ╱ ─ - ── ________ ________ ╱ ─ - ──
8 8 ╲╱ 8 8 ╱ 5 √5 ╱ √5 5 ⅈ ╲╱ 8 8
───────── + ─────────────── - ⅈ⋅ ╱ ─ - ── ⋅ ╱ ── + ─ - ─, - ────────────
4 4 ╲╱ 8 8 ╲╱ 8 8 4 4
________ ________ ________
╱ √5 5 ╱ 5 √5 ╱ √5 5
╱ ── + ─ √5⋅ ╱ ─ - ── √5⋅ ╱ ── + ─ ________ ______
╲╱ 8 8 ╲╱ 8 8 ╲╱ 8 8 ╱ 5 √5 ╱ √5
+ ──────────── + ─────────────── + ─────────────── - ⅈ⋅ ╱ ─ - ── ⋅ ╱ ── +
4 4 4 ╲╱ 8 8 ╲╱ 8
⎤
⎥
__ ⎥
5 ⅈ⎥
─ + ─⎥
8 4⎦
6. Průchod nulovými body periodické funkce
Přejděme nyní od polynomů k dalším funkcím, například k funkcím goniometrickým. Funkci solve je totiž možné mj. použít i pro vyhledání takových hodnot x goniometrické funkce cos, kdy je hodnota funkce nulová, tj. když graf funkce protíná osu x. Pokud ovšem použijeme funkci solve, nebudou nalezena všechna řešení, což je patrné i z následujícího příkladu:
from sympy import solve, symbols, pprint, init_printing, cos
init_printing(use_unicode=True)
x = symbols('x')
f = cos(x)
pprint(f)
solution = solve(f, x)
pprint(solution)
Z výsledku je patrné, že funkce solve v tomto případě vrátí pouze dvě hodnoty x a nikoli všechna možná řešení, kdy je hodnota periodické funkce nulová:
cos(x) ⎡π 3⋅π⎤ ⎢─, ───⎥ ⎣2 2 ⎦
7. Vyhledání všech možných řešení
Z předchozí kapitoly je zřejmé, že funkce solve v některých případech nevrátí všechna řešení, tj. typicky ty hodnoty x, pro které je hodnota funkce nulová. Můžeme však namísto toho použít funkci solveset:
Help on function solveset in module sympy.solvers.solveset:
solveset(f, symbol=None, domain=Complexes)
Solves a given inequality or equation with set as output
Parameters
==========
f : Expr or a relational.
The target equation or inequality
symbol : Symbol
The variable for which the equation is solved
domain : Set
The domain over which the equation is solved
Returns
=======
Set
A set of values for `symbol` for which `f` is True or is equal to
zero. An :class:`~.EmptySet` is returned if `f` is False or nonzero.
A :class:`~.ConditionSet` is returned as unsolved object if algorithms
to evaluate complete solution are not yet implemented.
``solveset`` claims to be complete in the solution set that it returns.
Zkusme tedy použít solveset namísto solve pro goniometrickou funkci cos:
from sympy import solveset, symbols, pprint, init_printing, cos
init_printing(use_unicode=True)
x = symbols('x')
f = cos(x)
pprint(f)
solution = solveset(f, x)
pprint(solution)
Výsledkem bude skutečně definice množiny (resp. přesněji řečeno sjednocení dvou množin) se všemi hodnotami, pro které je cos nulová:
cos(x) ⎧ π │ ⎫ ⎧ 3⋅π │ ⎫ ⎨2⋅n⋅π + ─ │ n ∊ ℤ⎬ ∪ ⎨2⋅n⋅π + ─── │ n ∊ ℤ⎬ ⎩ 2 │ ⎭ ⎩ 2 │ ⎭
8. Vyhledání řešení pro funkci sinc
V dalším demonstračním příkladu si ukážeme, jakým způsobem jsou vyhledány nulové body pro známou funkci sinc, kterou lze rozepsat do tvaru sin(x)/x. Průběh této funkce se od běžného sinu pochopitelně odlišuje (postupně dochází k utlumení), ovšem důležitá je taktéž hodnota funkce v bodě x=0, kde je jen definitoricky (a v limitě) určeno, že hodnota funkce je rovna jedné:
from sympy import solve, solveset, symbols, pprint, init_printing, sin
init_printing(use_unicode=True)
x = symbols('x')
f = sin(x)/x
pprint(f)
print()
solution = solve(f, x)
pprint(solution)
print()
solution = solveset(f, x)
pprint(solution)
Podívejme se nyní na výsledky. Funkce solve vrátí pouze jediný výsledek π, zatímco funkce solveset správně určí celou množinu hodnot x, která neobsahuje nulu (nelze zde použít N, tedy přirozená čísla, protože potřebujeme i záporné hodnoty n, nehledě na to, že není stále určeno, zda 0 je či není přirozené číslo):
sin(x)
──────
x
[π]
({2⋅n⋅π │ n ∊ ℤ} \ {0}) ∪ ({2⋅n⋅π + π │ n ∊ ℤ} \ {0})
9. Řešení jednoduché nerovnice
Funkce solve i solveset můžeme použít i pro vyřešení jednoduché nerovnice, konkrétně pro zjištění, pro jaké hodnoty x je nerovnost platná. Začněme velmi jednoduchým příkladem s nerovnicí x > 10, kterou je pochopitelně snadné vyřešit i ručně:
from sympy import solve, solveset, symbols, pprint, init_printing
init_printing(use_unicode=True)
x = symbols('x')
f = x > 10
pprint(f)
print()
solution = solve(f, x)
pprint(solution)
print()
solution = solveset(f, x)
pprint(solution)
Tento skript po svém spuštění nejdříve vypíše původní nerovnici a posléze i výsledky získané funkcemi solve a solveset:
x > 10
10 < x ∧ x < ∞
{x │ x ∊ ℂ ∧ (x > 10)}
Zde záleží jen na zadání, který výsledek má být použit – zda ten ve formě nerovnosti (zajímavé je přidání podmínky horního limitu, kterou bych asi nikdy ručně explicitně nezapisoval) či výsledek ve formě množiny (to, že x může být komplexní číslo, lze dalšími parametry upravit, například určením, jakého typu x skutečně je. Alternativně lze určit tzn. doménu pro funkci solveset).
10. Vyřešení složitější nerovnice
V některých případech nemusí být zápis zcela jednoznačný. Podívejme se například, co se stane, pokud se budeme snažit vyřešit nerovnici sin(x) > 10 (nebo klidně sin(x) > 1/2, na konstantě příliš nezáleží). Zavoláme přitom jak funkci solve, tak i solveset:
from sympy import solve, solveset, symbols, pprint, init_printing, sin
init_printing(use_unicode=True)
x = symbols('x')
f = sin(x) > 10
pprint(f)
print()
solution = solve(f, x)
pprint(solution)
print()
solution = solveset(f, x)
pprint(solution)
Výsledek bude v takovém případě neuspokojivý:
sin(x) > 10
False
{x │ x ∊ ℂ ∧ (sin(x) > 10)}
Ovšem ani pokus o vyřešení nerovnice, která může být pro určité intervaly hodnot x splněna, nedá uspokojivý (a ani správný) výsledek:
f = sin(x) < 0.5 solve(f, x) 0 ≤ x ∧ x < 2⋅π
Správné řešení si ukážeme příště.
Mimochodem – ještě více matoucí je chování operátoru ==, který porovnává výrazy na totožnost, nikoli na ekvivalenci. O tomto problému se opět zmíníme v navazujícím článku.
11. Vyřešení soustavy nerovnic
Funkci solve můžeme využít i k vyřešení soustavy několika nerovnic. Opět se podívejme na velmi jednoduchý příklad se dvěma nerovnicemi, každá se stejnou proměnnou x. Při volání funkce solve se obě nerovnice (nebo i větší počet nerovnic) předává v n-tici nebo v seznamu jako první parametr (druhý parametr totiž obsahuje symbol, pro který je řešení vypočteno):
from sympy import solve, solveset, symbols, pprint, init_printing
init_printing(use_unicode=True)
x = symbols('x')
f1 = x > 10
f2 = x < 20
pprint(f1)
pprint(f2)
print()
solution = solve((f1, f2), x)
pprint(solution)
Tato jednoduchá soustava nerovnic má jednoznačné řešení:
x > 10 x < 20 10 < x ∧ x < 20
12. Složitější soustava nerovnic
Samozřejmě nám nic nebrání v pokusu o vyřešení složitější soustavy nerovnic, například takových nerovnic, v nichž se vyskytují mocniny atd. Podívejme se tedy na příklad s nerovnicemi, v nichž jsou použity výrazy x2 a x3:
from sympy import solve, solveset, symbols, pprint, init_printing
init_printing(use_unicode=True)
x = symbols('x')
f1 = x**2 < 10
f2 = x**3 > -10
pprint(f1)
pprint(f2)
print()
solution = solve((f1, f2), x)
pprint(solution)
Nalezené řešení:
2 x < 10 3 x > -10 3 ____ -╲╱ 10 < x ∧ x < √10
13. Knihovna SymPy a Jupyter Notebook
Všechny demonstrační příklady, které jsme si doposud ukázali v úvodním článku i v předchozích kapitolách, vypisovaly svůj výsledek (i když většinou v takzvané pretty-printované podobě) na klasický textový terminál. I přesto, že jsou pro některé matematické symboly použity speciální (k tomu určené) znaky Unicode, není výstup v žádném případě perfektní a nelze ho s úspěchem použít v článcích atd. Knihovna SymPy nicméně podporuje výstup do TeXu/LaTeXu (což uvidíme dále) i do MathML. To má dvě přednosti – výstup lze zařadit do článků a taktéž je možné výsledky výpočtů zobrazit v Jupyter Notebooku, a to v nejvyšší dostupné kvalitě. V následujících kapitolách si nejprve ukážeme výsledky výpočtů zobrazených v Jupyter Notebooku a poté si ukážeme i přímý výstup do TeXu/LaTeXu.
14. Instalace Jupyter Notebooku
Jupyter Notebook je možné nainstalovat hned několika způsoby, podle toho, zda se využijí balíčky dostupné přímo v repositáři dané linuxové distribuce nebo se použijí jiní správci balíčků (conda, pip). Prakticky všechny oficiálně podporované postupy instalace jsou zmíněny v diagramu umístěném na stránce https://jupyter.readthedocs.io/en/latest/projects/content-projects.html.
Ve Fedoře (27 a výše) lze instalaci provést příkazem (podobné to bude i v distribucích založených na debianních balíčcích, akorát se pochopitelně použije jiný nástroj než dnf):
$ sudo dnf install python3-notebook
Příklad pro Fedoru 34:
Last metadata expiration check: 0:53:06 ago on Wed 25 May 2022 01:39:27 AM EDT. Dependencies resolved. ================================================================================ Package Architecture Versi ================================================================================ Installing: python3-notebook noarch 6.1.6
Nainstaluje se i velké množství závislých knihoven a balíčků:
Installing dependencies: ImageMagick-c++ x86_64 1:6.9 ImageMagick-libs x86_64 1:6.9 LibRaw x86_64 0.20. adobe-mappings-cmap noarch 20190 adobe-mappings-cmap-deprecated noarch 20190 adobe-mappings-pdf noarch 20190 atkmm x86_64 2.28. blosc x86_64 1.21. python3-xlrd noarch 2.0.1-2.fc34 beaker-Fedora 171 k python3-xlwt noarch 1.3.0-1.fc34 updates 200 k texlive-dvipng x86_64 9:20200327-30.fc34 updates 319 k Transaction Summary ================================================================================ Install 250 Packages Total download size: 271 M Installed size: 988 M Is this ok [y/N]: ImageMagick-c++ x86_64 1:6.9 ImageMagick-libs x86_64 1:6.9 LibRaw x86_64 0.20. adobe-mappings-cmap noarch 20190 adobe-mappings-cmap-deprecated noarch 20190 adobe-mappings-pdf noarch 20190 atkmm x86_64 2.28. blosc x86_64 1.21. Is this ok [y/N]:
Instalace na Linux Mintu a dalších distribucích odvozených od Ubuntu nebo Debianu probíhá prakticky stejným způsobem (i když je použit zcela odlišný systém balíčků):
$ sudo apt-get install python3-notebook
Samozřejmě se i v tomto případě nainstaluje i velká řada podpůrných balíčků:
Reading package lists... Done Building dependency tree Reading state information... Done The following additional packages will be installed: fonts-font-awesome fonts-glyphicons-halflings javascript-common jupyter-core jupyter-nbextension-jupyter-js-widgets jupyter-notebook libjs-backbone libjs-bootstrap libjs-bootstrap-tour libjs-codemirror libjs-es6-promise libjs-jed libjs-jquery libjs-jquery-typeahead libjs-jquery-ui libjs-marked libjs-moment libjs-requirejs libjs-requirejs-text libjs-text-encoding libjs-underscore libjs-xterm pandoc pandoc-data python3-attr python3-bleach python3-dateutil python3-defusedxml python3-html5lib python3-importlib-metadata python3-ipykernel python3-ipywidgets python3-jinja2 python3-jsonschema python3-jupyter-client python3-jupyter-core python3-mistune python3-more-itertools python3-nbconvert python3-nbformat python3-pandocfilters python3-prometheus-client python3-pyrsistent python3-send2trash python3-terminado python3-testpath python3-tornado python3-webencodings python3-widgetsnbextension python3-zipp python3-zmq Suggested packages: apache2 | lighttpd | httpd libjs-jquery-lazyload libjs-json libjs-jquery-ui-docs texlive-latex-recommended texlive-xetex texlive-luatex pandoc-citeproc texlive-latex-extra context wkhtmltopdf librsvg2-bin groff ghc nodejs php python ruby r-base-core node-katex python-attr-doc python-bleach-doc python3-genshi python3-lxml python-ipywidgets-doc python-jinja2-doc python-jsonschema-doc python-nbconvert-doc python-notebook-doc python-tornado-doc python3-twisted The following NEW packages will be installed: fonts-font-awesome fonts-glyphicons-halflings javascript-common jupyter-core jupyter-nbextension-jupyter-js-widgets jupyter-notebook libjs-backbone libjs-bootstrap libjs-bootstrap-tour libjs-codemirror libjs-es6-promise libjs-jed libjs-jquery libjs-jquery-typeahead libjs-jquery-ui libjs-marked libjs-moment libjs-requirejs libjs-requirejs-text libjs-text-encoding libjs-underscore libjs-xterm pandoc pandoc-data python3-attr python3-bleach python3-dateutil python3-defusedxml python3-html5lib python3-importlib-metadata python3-ipykernel python3-ipywidgets python3-jinja2 python3-jsonschema python3-jupyter-client python3-jupyter-core python3-mistune python3-more-itertools python3-nbconvert python3-nbformat python3-notebook python3-pandocfilters python3-prometheus-client python3-pyrsistent python3-send2trash python3-terminado python3-testpath python3-tornado python3-webencodings python3-widgetsnbextension python3-zipp python3-zmq 0 upgraded, 52 newly installed, 0 to remove and 424 not upgraded. Need to get 21,1 MB of archives. After this operation, 165 MB of additional disk space will be used. Do you want to continue? [Y/n]
Využít je možné i správce balíčků Conda. V případě, že tento nástroj používáte, bude instalace vypadat následovně:
$ conda install -c conda-forge notebook
A konečně lze použít i klasický pip nebo pip3 (v závislosti na tom, jaký je stav Pythonu 3 na daném operačním systému):
$ pip install notebook
V případě, že pip instaluje balíčky pro Python 2 a nikoli pro Python 3, použijeme:
$ pip3 install notebook
Použít je možné i spuštění v kontejneru. Konkrétně pro Docker je k dispozici hned několik obrazů Jupyter Notebooku, každý s rozdílnými kernely a dalšími moduly. Viz https://hub.docker.com/u/jupyter/#!.
15. Nastavení Jupyter Notebooku
Ještě před prvním spuštěním Jupyter Notebooku je vhodné si nastavit heslo, které se bude zadávat pro přístup do jeho grafického uživatelského rozhraní:
$ jupyter notebook password Enter password: Verify password: [NotebookPasswordApp] Wrote hashed password to /home/ptisnovs/.jupyter/jupyter_notebook_config.json
Nyní konečně nastal čas spustit Jupyter Notebook:
$ jupyter notebook [I 02:44:07.823 NotebookApp] Writing notebook server cookie secret to /home/tester/.local/share/jupyter/runtime/notebook_cookie_secret [C 02:44:08.404 NotebookApp] Running as root is not recommended. Use --allow-root to bypass. [root@hpe-dl380pgen8-02-vm-15 ~]# jupyter notebook --allow-root [I 02:44:23.193 NotebookApp] Serving notebooks from local directory: /home/tester [I 02:44:23.193 NotebookApp] Jupyter Notebook 6.1.6 is running at: [I 02:44:23.193 NotebookApp] http://localhost:8888/ [I 02:44:23.193 NotebookApp] Use Control-C to stop this server and shut down all kernels (twice to skip confirmation).
Současně by se ve webovém prohlížeči měl otevřít další tab s úvodní obrazovkou Jupyter Notebooku určenou pro přihlášení. Po přihlášení (heslo jsme nastavili v předchozím kroku) se otevře okno, v němž je možné vytvořit nový sešit/diář (New) nebo otevřít sešit již existující:

Obrázek 1: První spuštění Jupyter Notebooku.
16. Ukázky použití knihovny SymPy v Jupyter Notebooku
Podívejme se nyní na to, jakým způsobem se změní výstup skriptů, s nimiž jsme se již seznámili v rámci úvodního článku popř. předchozích kapitol:

Obrázek 2: Výstup, který vlastně napodobuje klasický terminál s fontem s podporou Unicode.

Obrázek 3: Ovšem tento výraz je již zobrazen v „pravé matematické“ notaci.
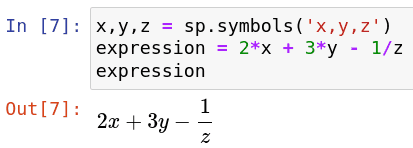
Obrázek 4: Způsob zobrazení zlomků v matematické notaci.

Obrázek 5: Mocniny, výrazy v mocninách (exponentu) a zlomky v jediném výrazu.
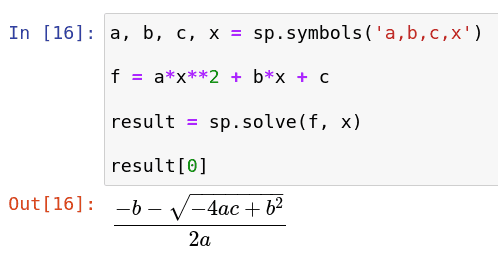
Obrázek 6: Symbolické vyjádření kořenů kvadratické rovnice (resp. jednoho z kořenů).

Obrázek 7: Derivace výrazu.

Obrázek 8: Množina (sjednocení dvou množin) s vyjádřením všech hodnot x, pro které funkce cos nabývá nulové hodnoty.
17. Vykreslení grafů knihovnou SymPy
Knihovna SymPy podporuje i vykreslení grafů. Opět se podívejme na několik ukázek. Vstupem pro vykreslení grafu je ve všech případech symbolický zápis nějaké funkce – buď funkce přímo zapsané uživatelem, nebo se jedná o výsledek výpočtu, například derivace nebo integrace:
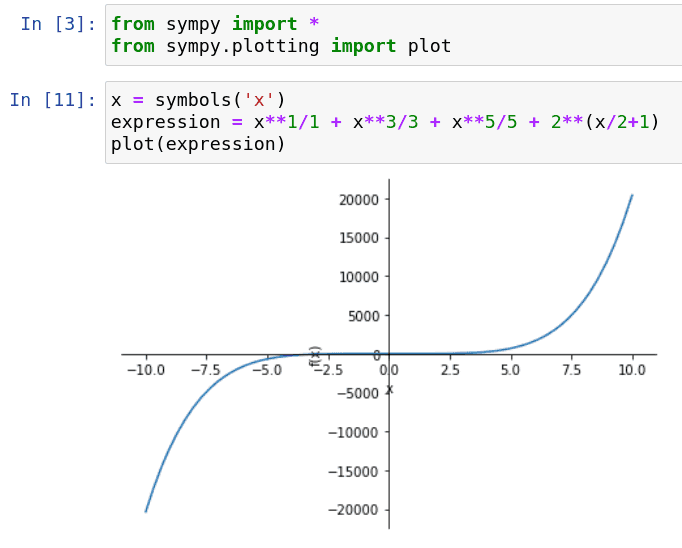
Obrázek 9: Vykreslení průběhu funkce.
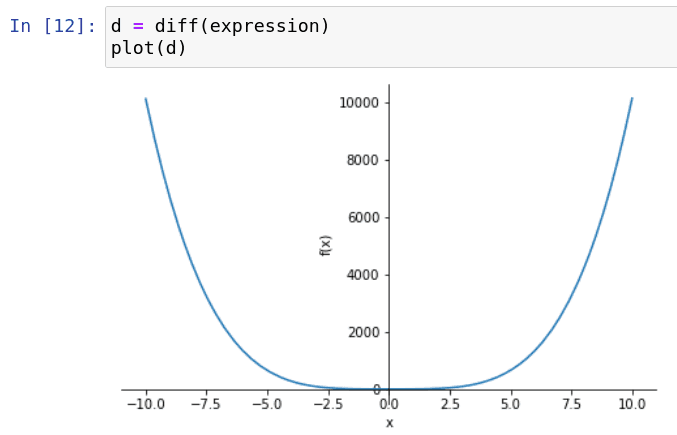
Obrázek 10: Takto vypadá derivace předchozí funkce.
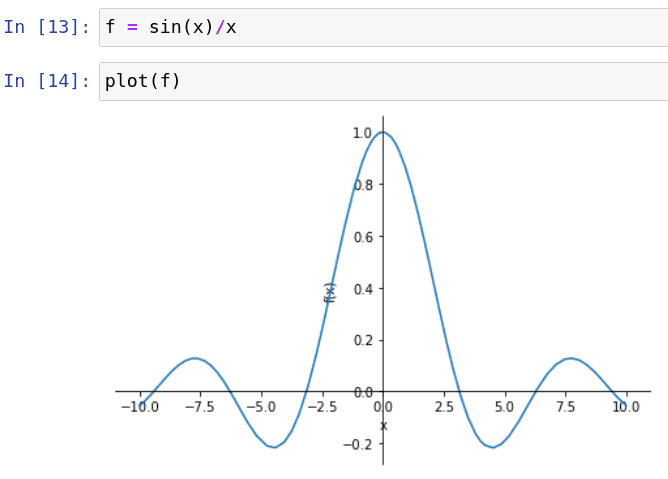
Obrázek 11: Průběh funkce sinc.
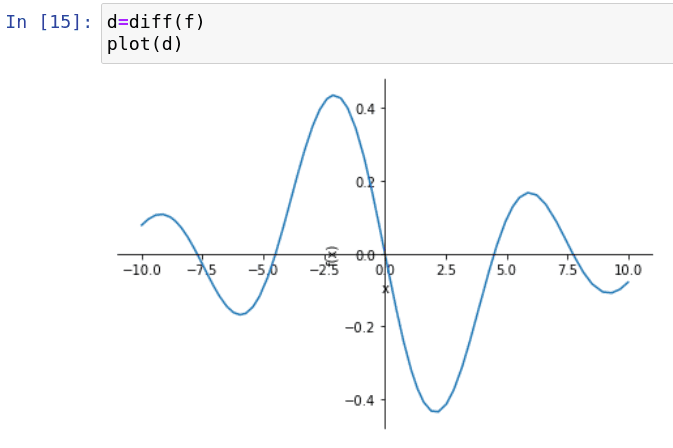
Obrázek 12: Derivace funkce sinc.
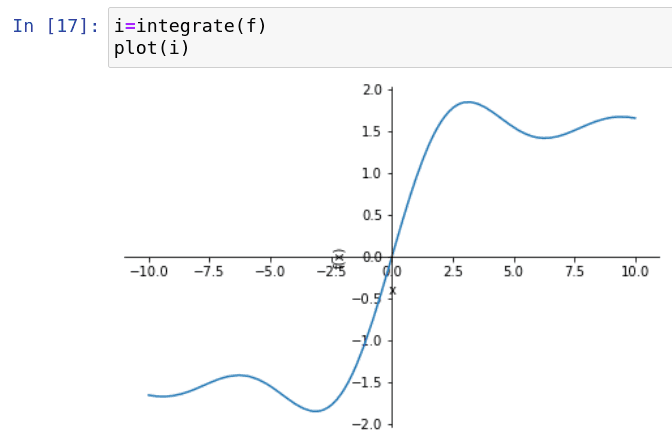
Obrázek 13: Integrace funkce sinc.
18. Výstup do TeXu/LaTeXu
V krátkosti se ještě podívejme na způsob výstupu do TeXu nebo LaTeXu. Postačuje použít funkci nazvanou latex, které se předá výraz, jenž se má zkopírovat do dokumentu (například do článku). Vraťme se k řešení kořenů kvadratické rovnice. Symbolický výsledek budeme chtít zkopírovat do LaTeXového dokumentu:
a, b, c, x = symbols('a,b,c,x')
f = a*x**2 + b*x + c
print(latex(solve(f, x)))
S výsledkem:
\left[ \frac{- b + \sqrt{- 4 a c + b^{2}}}{2 a}, \ - \frac{b + \sqrt{- 4 a c + b^{2}}}{2 a}\right]
Nebo složitější příklad:
f=x**10 + 1 print(latex(solve(f,x)))
Se sáhodlouhým, ovšem korektním výsledkem:
\left[ - \sqrt{\frac{\sqrt{5}}{8} + \frac{5}{8}} - \frac{\sqrt{5} i}{4} + \frac{i}{4},
\ \sqrt{\frac{\sqrt{5}}{8} + \frac{5}{8}} - \frac{i}{4} + \frac{\sqrt{5} i}{4},
\ - \frac{\sqrt{5} \sqrt{\frac{\sqrt{5}}{8} + \frac{5}{8}}}{2} +
\frac{\sqrt{\frac{\sqrt{5}}{8} + \frac{5}{8}}}{2} + \frac{i}{4} + \frac{\sqrt{5} i}{4},
\ - \frac{\sqrt{\frac{\sqrt{5}}{8} + \frac{5}{8}}}{2} +
...
...
...
+ \frac{5}{8}} + \frac{i}{4}\right]
19. Repositář s demonstračními příklady
Zdrojové kódy všech prozatím popsaných demonstračních příkladů určených pro programovací jazyk Python 3 byly uloženy do Git repositáře dostupného na adrese https://github.com/tisnik/most-popular-python-libs. V případě, že nebudete chtít klonovat celý repositář (ten je ovšem stále velmi malý, dnes má velikost zhruba několik desítek kilobajtů), můžete namísto toho použít odkazy na jednotlivé příklady, které naleznete v následující tabulce:
20. Odkazy na Internetu
- SymPy
https://www.sympy.org/en/index.html - SymPy na PyPi
https://pypi.org/project/sympy/ - mpmath
https://mpmath.org/ - mpmath na PyPi
https://pypi.org/project/mpmath/ - Symbolic Maths in Python
https://alexandrugris.github.io/maths/2017/04/30/symbolic-maths-python.html - SymPy shell
https://live.sympy.org/ - Symbolic programming
https://en.wikipedia.org/wiki/Symbolic_programming - Symbolic language (programming)
https://en.wikipedia.org/wiki/Symbolic_language_(programming) - Computer algebra
https://en.wikipedia.org/wiki/Computer_algebra - Common Lisp: A Gentle Introduction to Symbolic Computation
https://www.cs.cmu.edu/~dst/LispBook/ - List of computer algebra systems
https://en.wikipedia.org/wiki/List_of_computer_algebra_systems - Polynom
https://cs.wikipedia.org/wiki/Polynom - What is SimPy? How to run python simulations?
https://divyas090909.medium.com/what-is-simpy-how-to-run-python-simulations-348736b50615 - SimPy: Simulating Real-World Processes With Python
https://realpython.com/simpy-simulating-with-python/






































