Tisk hexadecimálních hodnot s využitím instrukce DAA na ZX Spectru

20. 4. 2023

Doba čtení: 47 minut

Líbí se vám článek?
Podpořte redakci

Dnešní článek o vývoji programů pro mikropočítač ZX Spectrum je rozdělen na dvě části. V úvodní části si ukážeme využití instrukce DAA při tisku hexadecimálních hodnot a v části druhé se seznámíme se základy zpracování hodnot s plovoucí řádovou čárkou.

Obsah

1. Tisk hexadecimálních hodnot podruhé

2. Úplný zdrojový kód dnešního prvního demonstračního příkladu

3. Malá odbočka: přetečení hodnoty cifry

4. Úplný zdrojový kód dnešního druhého demonstračního příkladu

5. Využití instrukce DAA namísto podmíněného skoku

6. Podrobný popis operací prováděných při převodu hexadecimální cifry na ASCII znak

7. Úplný zdrojový kód dnešního třetího demonstračního příkladu

8. Vylepšené vytištění osmibitové hexadecimální hodnoty

9. Úplný zdrojový kód dnešního čtvrtého demonstračního příkladu

10. Reprezentace numerických hodnot ve formátu pevné a plovoucí řádové (binární) tečky

11. Vybrané způsoby reprezentace numerických hodnot v operační paměti počítače

12. Uložení numerických hodnot ve formátu pevné řádové binární tečky

13. Přednosti a zápory formátu pevné řádové tečky

14. Uložení čísel ve formátu plovoucí řádové (binární) tečky

15. Formát uložení FP hodnot na ZX Spectru

16. Zásobník FP hodnot na ZX Spectru, subrutina pro tisk FP hodnot

17. Úplný zdrojový kód dnešního pátého demonstračního příkladu

18. Příloha: upravený soubor Makefile pro překlad demonstračních příkladů

19. Repositář s demonstračními příklady

20. Odkazy na Internetu

1. Tisk hexadecimálních hodnot podruhé

V dnešním článku si nejprve ukážeme trik pro tisk hexadecimálních hodnot. Tento trik je založen na instrukci DAA a osmibitové aritmetice. A posléze se zaměříme na zcela odlišnou oblast – jak se dá pracovat s numerickými hodnotami reprezentovanými v systému pevné i plovoucí řádové tečky (fixed point, floating point).

Zaměřme se nyní na způsob zobrazení jediné hexadecimální cifry, tj. znaku „0“, „1“,… „9“, „A“ … „F“. Úloha je to vlastně velmi snadná: na vstupu budeme mít hodnotu 0 až 15 uloženou v akumulátoru A a výsledkem má být jeden z výše zmíněných znaků vytisknutých na obrazovku ZX Spectra. Znaky pro tisk se přitom pochopitelně vybírají z ASCII tabulky resp. přesněji řečeno z její „spektrácké“ verze, která vypadá následovně:

Autor: tisnik, podle licence: <a href="http://en.wikipedia.org/wiki/Rights_Managed">Rights Managed</a>

Obrázek 1: „Spektrácká“ verze ASCII tabulky (zobrazeny jsou jen tisknutelné znaky).

Jediný problém spočívá v tom, že převod hodnoty 0 až 15 na kód znaku není zcela přímočarý, protože znaky jsou v ASCII kódu uspořádány takovým způsobem, že se mezi znakem „9“ a znakem „A“ nachází sedm jiných znaků, konkrétně znaky „:“, „;“, „<“, „=“, „>“, „?“ a „@“:

Obrázek 2: Hexadecimální cifry nejsou v ASCII umístěny za sebou.

K dispozici jsou tři rozumná řešení:

Použití převodní tabulky (ovšem ztratíme šestnáct bajtů RAM + další bajty pro kód)
Použití podmínky + skoku, který řeší „mezeru“
Aritmetické triky zajišťující, že se pro hodnoty vyšší než 9 provede operace +7

Druhý způsob už jsme si ukázali minule, ale pro jistotu si ho ještě zopakujme. Princip je jednoduchý – vypočteme ASCII hodnotu znaku tak, jakoby byly všechny cifry umístěny za sebou a posléze provedeme úpravu +7 pro cifry s hodnotou vyšší než 9:

print_hex_digit_nl:
        push AF             ; uschovat A pro pozdější využití
 
        cp   0x0a           ; test, jestli je číslice menší než 10
        jr c, print_0_to_9  ; ok, hodnota je menší než 10, budeme tedy tisknout desítkovou číslici
        add  A, 65-10-48    ; ASCII kód znaku 'A', ovšem začínáme od desítky, ne od nuly (+ update pro další ADD)
print_0_to_9:
        add  A, 48          ; ASCII kód znaku '0'
        rst  0x10           ; zavolání rutiny v ROM pro tisk jednoho znaku
 
new_line:
        ld   A, 0x0d        ; kód znaku pro odřádkování
        rst  0x10           ; zavolání rutiny v ROM
        pop  AF             ; obnovit A
        ret                 ; návrat ze subrutiny

2. Úplný zdrojový kód dnešního prvního demonstračního příkladu

Výše uvedený kód je použit pro tisk těchto hodnot:

Obrázek 3: Hexadecimální cifry vypočtené a zobrazené dnešním prvním demonstračním příkladem.

Úplný zdrojový kód demonstračního příkladu popsaného v úvodní kapitole je dostupný na adrese https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/79-print-hex-digit-jmp.asm:

ENTRY_POINT   equ $8000
ROM_CLS       equ $0DAF
OUT_NUM_1     equ $1A1B
 
 
        org ENTRY_POINT
 
start:
        call ROM_CLS        ; smazání obrazovky a otevření kanálu číslo 2 (screen)
 
        xor  A              ; hodnota cifry, která se má vytisknout
        ld   B, 16          ; počitadlo smyčky
loop:                       ; vytisknout hexa cifru s přechodem na nový řádek
        call print_hex_digit_nl
        inc  A              ; zvýšit hodnotu tištěné cifry
        djnz loop           ; opakování smyčky se snížením hodnoty počitadla
 
        ret                 ; návrat z programu do BASICu
 
print_hex_digit_nl:
        push AF             ; uschovat A pro pozdější využití
 
        cp   0x0a           ; test, jestli je číslice menší než 10
        jr c, print_0_to_9  ; ok, hodnota je menší než 10, budeme tedy tisknout desítkovou číslici
        add  A, 65-10-48    ; ASCII kód znaku 'A', ovšem začínáme od desítky, ne od nuly (+ update pro další ADD)
print_0_to_9:
        add  A, 48          ; ASCII kód znaku '0'
        rst  0x10           ; zavolání rutiny v ROM pro tisk jednoho znaku
 
new_line:
        ld   A, 0x0d        ; kód znaku pro odřádkování
        rst  0x10           ; zavolání rutiny v ROM
        pop  AF             ; obnovit A
        ret                 ; návrat ze subrutiny
 
 
end ENTRY_POINT

Samozřejmě si opět pro úplnost ukážeme, jak byl tento zdrojový text přeložen do strojového kódu:

ENTRY_POINT     EQU 8000
ROM_CLS         EQU 0DAF
OUT_NUM_1       EQU 1A1B
                ORG 8000
8000:           label start
8000:CDAF0D     CALL 0DAF
8003:AF         XOR A
8004:0610       LD B, 10
8006:           label loop
8006:CD0D80     CALL 800D
8009:3C         INC A
800A:10FA       DJNZ 8006
800C:C9         RET
800D:           label print_hex_digit_nl
800D:F5         PUSH AF
800E:FE0A       CP 0A
8010:3802       JR C, 8014
8012:C607       ADD A, 07
8014:           label print_0_to_9
8014:C630       ADD A, 30
8016:D7         RST 10
8017:           label new_line
8017:3E0D       LD A, 0D
8019:D7         RST 10
801A:F1         POP AF
801B:C9         RET
801C:           END 8000
Emiting TAP basic loader
Emiting TAP from 8000 to 801B

3. Malá odbočka: přetečení hodnoty cifry

Zajímavé bude si vyzkoušet, co se stane ve chvíli, kdy se pokusíme o převod a vytištění dekadické hodnoty větší než 15. Velmi snadno si můžeme upravit počítanou programovou smyčku v předchozím příkladu takovým způsobem, aby se smyčka nezastavila na hodnotě 15, ale až na hodnotě 19 (více řádků se již nevytiskne, protože se ROM rutina zastaví a čeká na vstup od uživatele):

        xor  A              ; hodnota cifry, která se má vytisknout
        ld   B, 20          ; počitadlo smyčky
loop:                       ; vytisknout hexa cifru s přechodem na nový řádek
        call print_hex_digit_nl
        inc  A              ; zvýšit hodnotu tištěné cifry
        djnz loop           ; opakování smyčky se snížením hodnoty počitadla

Z výsledků je patrné, že se vypisují další cifry „G“ atd. až do „Z“, což vlastně znamená, že máme k dispozici rutinu platnou pro třiceti šestkovou číselnou soustavu (10 numerických znaků + 26 znaků anglické abecedy):

Obrázek 4: Tisk „hexadecimálních“ hodnot odpovídajících dekadickým hodnotám od 0 do 19. Povšimněte si, že ve skutečnosti máme k dispozici celou 36 číselnou soustavu.

Poznámka: řešení představené v dalším textu již bude jiné a bude skutečně platné pouze pro hexadecimální soustavu.

4. Úplný zdrojový kód dnešního druhého demonstračního příkladu

Úplný zdrojový kód dnešního druhého demonstračního příkladu je dostupný na adrese https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/80-print-hex-digit-overflow.asm:

ENTRY_POINT   equ $8000
ROM_CLS       equ $0DAF
OUT_NUM_1     equ $1A1B
 
 
        org ENTRY_POINT
 
start:
        call ROM_CLS        ; smazání obrazovky a otevření kanálu číslo 2 (screen)
 
        xor  A              ; hodnota cifry, která se má vytisknout
        ld   B, 20          ; počitadlo smyčky
loop:                       ; vytisknout hexa cifru s přechodem na nový řádek
        call print_hex_digit_nl
        inc  A              ; zvýšit hodnotu tištěné cifry
        djnz loop           ; opakování smyčky se snížením hodnoty počitadla
 
        ret                 ; návrat z programu do BASICu
 
print_hex_digit_nl:
        push AF             ; uschovat A pro pozdější využití
 
        cp   0x0a           ; test, jestli je číslice menší než 10
        jr c, print_0_to_9  ; ok, hodnota je menší než 10, budeme tedy tisknout desítkovou číslici
        add  A, 65-10-48    ; ASCII kód znaku 'A', ovšem začínáme od desítky, ne od nuly (+ update pro další ADD)
print_0_to_9:
        add  A, 48          ; ASCII kód znaku '0'
        rst  0x10           ; zavolání rutiny v ROM pro tisk jednoho znaku
 
new_line:
        ld   A, 0x0d        ; kód znaku pro odřádkování
        rst  0x10           ; zavolání rutiny v ROM
        pop  AF             ; obnovit A
        ret                 ; návrat ze subrutiny
 
 
end ENTRY_POINT

Způsob překladu do strojového kódu je prakticky totožný s příkladem prvním (a to zcela podle očekávání):

ENTRY_POINT     EQU 8000
ROM_CLS         EQU 0DAF
OUT_NUM_1       EQU 1A1B
                ORG 8000
8000:           label start
8000:CDAF0D     CALL 0DAF
8003:AF         XOR A
8004:0614       LD B, 14
8006:           label loop
8006:CD0D80     CALL 800D
8009:3C         INC A
800A:10FA       DJNZ 8006
800C:C9         RET
800D:           label print_hex_digit_nl
800D:F5         PUSH AF
800E:FE0A       CP 0A
8010:3802       JR C, 8014
8012:C607       ADD A, 07
8014:           label print_0_to_9
8014:C630       ADD A, 30
8016:D7         RST 10
8017:           label new_line
8017:3E0D       LD A, 0D
8019:D7         RST 10
801A:F1         POP AF
801B:C9         RET
801C:           END 8000
Emiting TAP basic loader
Emiting TAP from 8000 to 801B

5. Využití instrukce DAA namísto podmíněného skoku

Víme již, že problém, který řešíme, je následující: pro hodnoty větší než 9 musíme ASCII hodnotu příslušného znaku vypočítat posunutou o sedm pozic, protože takovým způsobem je uspořádána ASCII tabulka. Řešení spočívá v „chytrém“ použití instrukce DAA, která nám umožní automaticky (bez nutnosti použití podmíněného skoku) zvýšit hodnotu o 6. Zbývá nám pouze zajistit přičtení jedničky. K tomu slouží instrukce ADC, pro přičtení konstanty a případného přenosu (carry):

print_hex_digit_nl:
        push AF             ; uschovat A pro pozdější využití
        or   $f0            ; nastavit horní čtyři bity + příznaky
                            ; nyní je v A jedna z hodnot:
                            ;    0xf0 0xf1 0xf2 ... 0xf9 0xfa 0xfb 0xfc 0xfd 0xfe 0xff
        daa                 ; desítková korekce pro původní hodnoty A-F
                            ; +  0x60 0x60 0x60 ... 0x60 0x66 0x66 0x66 0x66 0x66 0x66
                            ; nyní je v A jedna z hodnot:
                            ;    0x50 0x51 0x52 ... 0x59 0x60 0x61 0x62 0x63 0x64 0x65
        add A, $a0          ; přičtení konstanty
                            ; nyní je v A jedna z hodnot:
                            ;    0xf0 0xf1 0xf2 ... 0xf9 0x00 0x01 0x02 0x03 0x04 0x05
                            ; C    0    0    0        0    1    1    1    1    1    1
        adc A, $40          ; přičtení konstanty a navíc i příznaku carry
                            ;    0x30 0x31 0x31 ... 0x39 0x41 0x42 0x43 0x44 0x45 0x46
                            ; >   '0'  '1'  '2'      '9'  'A'  'B'  'C'  'D'  'E'  'F'
        rst  0x10           ; zavolání rutiny v ROM pro tisk jednoho znaku

6. Podrobný popis operací prováděných při převodu hexadecimální cifry na ASCII znak

Výše uvedený kód provádí jak převod cifry na ASCII znak, tak i úpravu +7, tedy přeskočení těchto znaků:

Obrázek 5: Sedmice znaků v ASCII tabulce, které je nutné přeskočit.

Pojďme si nyní podrobněji popsat jednotlivé fáze výpočtu. Nejprve se pokusíme o převod hodnoty (cifry) 0, ovšem naprosto stejný popis bude platný i pro cifry od 1 do 9 (hodnoty jsou vždy uložené v akumulátoru a znak dolaru značí hexadecimální hodnotu):

Hodnota před instrukcí	Instrukce	Provedená operace	Hodnota po instrukci	Carry	Stručný popis
$00	or $f0	or $f0	$f0	0	nastavit horní čtyři bity
$f0	daa	$f0+$60	$50	1	desítková korekce pro horní čtyři bity (dolní jsou stále nulové)
$50	add A, $a0	$50+$a0	$f0	0	přičtení takové hodnoty, aby se nenastavil carry
$f0	adc A, $40	$f0+$40+0	$30	1	hodnota $30 skutečně odpovídá znaku „0“

Naproti tomu výpočet pro cifry A až F bude naprosto odlišný. Ukažme si to na hodnotě 0×0a (resp. kvůli větší konzistenci $0a):

Hodnota před instrukcí	Instrukce	Provedená operace	Hodnota po instrukci	Carry	Stručný popis
$0a	or $f0	or $f0	$fa	0	nastavit horní čtyři bity
$fa	daa	$fa+$66	$60	1	desítková korekce pro horní i dolní čtyři bity (kýžené přičtení +6)
$60	add A, $a0	$60+$a0	$00	1	přičtení takové hodnoty, aby se nastavil carry (kýžené přičtení +1)
$00	adc A, $40	$00+$40+1	$41	0	hodnota $41 skutečně odpovídá znaku „A“

Poznámka: a pak že programování v assembleru není krásné a elegantní.

7. Úplný zdrojový kód dnešního třetího demonstračního příkladu

Výše uvedený kód můžeme bez dalších úprav použít pro tisk hexadecimálních cifer 0 až F:

Obrázek 6: Cifry 0 až F vytištěné demonstračním příkladem.

Úplný zdrojový kód dnešního třetího demonstračního příkladu je dostupný na adrese https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/81-print-hex-digit-daa.asm:

ENTRY_POINT   equ $8000
ROM_CLS       equ $0DAF
OUT_NUM_1     equ $1A1B
 
 
        org ENTRY_POINT
 
start:
        call ROM_CLS        ; smazání obrazovky a otevření kanálu číslo 2 (screen)
 
        xor  A              ; hodnota cifry, která se má vytisknout
        ld   B, 16          ; počitadlo smyčky
loop:                       ; vytisknout hexa cifru s přechodem na nový řádek
        call print_hex_digit_nl
        inc  A              ; zvýšit hodnotu tištěné cifry
        djnz loop           ; opakování smyčky se snížením hodnoty počitadla
 
        ret                 ; návrat z programu do BASICu
 
print_hex_digit_nl:
        push AF             ; uschovat A pro pozdější využití
        or   $f0            ; nastavit horní čtyři bity + příznaky
                            ; nyní je v A jedna z hodnot:
                            ;    0xf0 0xf1 0xf2 ... 0xf9 0xfa 0xfb 0xfc 0xfd 0xfe 0xff
        daa                 ; desítková korekce pro původní hodnoty A-F
                            ; +  0x60 0x60 0x60 ... 0x60 0x66 0x66 0x66 0x66 0x66 0x66
                            ; nyní je v A jedna z hodnot:
                            ;    0x50 0x51 0x52 ... 0x59 0x60 0x61 0x62 0x63 0x64 0x65
        add A, $a0          ; přičtení konstanty
                            ; nyní je v A jedna z hodnot:
                            ;    0xf0 0xf1 0xf2 ... 0xf9 0x00 0x01 0x02 0x03 0x04 0x05
                            ; C    0    0    0        0    1    1    1    1    1    1
        adc A, $40          ; přičtení konstanty a navíc i příznaku carry
                            ;    0x30 0x31 0x31 ... 0x39 0x41 0x42 0x43 0x44 0x45 0x46
                            ; >   '0'  '1'  '2'      '9'  'A'  'B'  'C'  'D'  'E'  'F'
        rst  0x10           ; zavolání rutiny v ROM pro tisk jednoho znaku
 
new_line:
        ld   A, 0x0d        ; kód znaku pro odřádkování
        rst  0x10           ; zavolání rutiny v ROM
        pop  AF             ; obnovit A
        ret                 ; návrat ze subrutiny
 
 
end ENTRY_POINT

A pro úplnost se podívejme na způsob překladu výše uvedeného zdrojového kódu do assembleru:

ENTRY_POINT     EQU 8000
ROM_CLS         EQU 0DAF
OUT_NUM_1       EQU 1A1B
                ORG 8000
8000:           label start
8000:CDAF0D     CALL 0DAF
8003:AF         XOR A
8004:0610       LD B, 10
8006:           label loop
8006:CD0D80     CALL 800D
8009:3C         INC A
800A:10FA       DJNZ 8006
800C:C9         RET
800D:           label print_hex_digit_nl
800D:F5         PUSH AF
800E:F6F0       OR F0
8010:27         DAA
8011:C6A0       ADD A, A0
8013:CE40       ADC A, 40
8015:D7         RST 10
8016:           label new_line
8016:3E0D       LD A, 0D
8018:D7         RST 10
8019:F1         POP AF
801A:C9         RET
801B:           END 8000
Emiting TAP basic loader
Emiting TAP from 8000 to 801A

8. Vylepšené vytištění osmibitové hexadecimální hodnoty

Nyní, když již známe způsob efektivního převodu jedné hexadecimální cifry na ASCII znak, můžeme upravit původní demonstrační příklad, který tiskne osmibitovou hexadecimální hodnotu na obrazovku (a tedy dvě cifry). Nejprve se vytiskne vyšší cifra, poté cifra nižší. Povšimněte si, že podprogram print_hex_digit se volá jen jedenkrát – a to pro vyšší cifru. Pro nižší cifru není volání implementováno, protože podprogram print_hex_digit je umístěn přímo za print_hex_number, jak správně upozornil kolega _dw:

print_hex_number:
        push AF             ; uschovat A pro pozdější využití
        rrca                ; rotace o čtyři bity doprava
        rrca
        rrca
        rrca
        call print_hex_digit; vytisknout první hexa cifru
 
        pop  AF             ; obnovit A
                            ; vytisknout druhou hexa cifru
 
print_hex_digit:
        or   $f0            ; nastavit horní čtyři bity + příznaky
        daa                 ; desítková korekce pro původní hodnoty A-F
        add A, $a0          ; přičtení konstanty
        adc A, $40          ; přičtení konstanty a navíc i příznaku carry
        rst  0x10           ; zavolání rutiny v ROM pro tisk jednoho znaku
        ret                 ; návrat ze subrutiny

Výsledek bude vypadat následovně:

Obrázek 7: Několik osmibitových hexadecimálních hodnot vytištěných touto subrutinou.

9. Úplný zdrojový kód dnešního čtvrtého demonstračního příkladu

Úplný zdrojový kód dnešního čtvrtého demonstračního příkladu je dostupný na adrese https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/82-print-hex-numbers-daa.asm:

ENTRY_POINT   equ $8000
ROM_CLS       equ $0DAF
OUT_NUM_1     equ $1A1B
 
 
        org ENTRY_POINT
 
start:
        call ROM_CLS           ; smazání obrazovky a otevření kanálu číslo 2 (screen)
 
        ld   HL, numbers       ; statické pole s hodnotami, které se mají vytisknout + zarážkou
loop:
        ld   A, (HL)           ; načíst další hodnotu ze statického pole
        or   A                 ; test na nulu
        ret  z                 ; návrat z programu do BASICU
        inc  HL                ; adresa dalšího prvku v poli
        call print_hex_number  ; tisk hexadecimální hodnoty
        call new_line          ; s přechodem na nový řádek
        jp   loop              ; zpracování další hodnoty
 
numbers:
        db 0x01, 0x02, 0x09, 0x0a, 0x10, 0x99, 0xa0, 0xaa, 0xaf, 0xf0, 0xff, 0x00
 
print_hex_number:
        push AF             ; uschovat A pro pozdější využití
        rrca                ; rotace o čtyři bity doprava
        rrca
        rrca
        rrca
        call print_hex_digit; vytisknout první hexa cifru
 
        pop  AF             ; obnovit A
                            ; vytisknout druhou hexa cifru
 
print_hex_digit:
        or   $f0            ; nastavit horní čtyři bity + příznaky
        daa                 ; desítková korekce pro původní hodnoty A-F
        add A, $a0          ; přičtení konstanty
        adc A, $40          ; přičtení konstanty a navíc i příznaku carry
        rst  0x10           ; zavolání rutiny v ROM pro tisk jednoho znaku
        ret                 ; návrat ze subrutiny
 
new_line:
        ld   A, 0x0d        ; kód znaku pro odřádkování
        rst  0x10           ; zavolání rutiny v ROM
        ret                 ; návrat ze subrutiny
 
 
end ENTRY_POINT

A pro úplnost se opět podívejme na způsob překladu výše uvedeného zdrojového kódu do assembleru:

ENTRY_POINT     EQU 8000
ROM_CLS         EQU 0DAF
OUT_NUM_1       EQU 1A1B
                ORG 8000
8000:           label start
8000:CDAF0D     CALL 0DAF
8003:211380     LD HL, 8013
8006:           label loop
8006:7E         LD A, (HL)
8007:B7         OR A
8008:C8         RET Z
8009:23         INC HL
800A:CD1F80     CALL 801F
800D:CD3180     CALL 8031
8010:C30680     JP 8006
8013:           label numbers
8013:0102090A   DEFB of 12 bytes
8017:1099A0AA
801B:AFF0FF00
801F:           label print_hex_number
801F:F5         PUSH AF
8020:0F         RRCA
8021:0F         RRCA
8022:0F         RRCA
8023:0F         RRCA
8024:CD2880     CALL 8028
8027:F1         POP AF
8028:           label print_hex_digit
8028:F6F0       OR F0
802A:27         DAA
802B:C6A0       ADD A, A0
802D:CE40       ADC A, 40
802F:D7         RST 10
8030:C9         RET
8031:           label new_line
8031:3E0D       LD A, 0D
8033:D7         RST 10
8034:C9         RET
8035:           END 8000
Emiting TAP basic loader
Emiting TAP from 8000 to 8034

10. Reprezentace numerických hodnot ve formátu pevné a plovoucí řádové (binární) tečky

Ve druhé části dnešního článku si ve stručnosti popíšeme některé ze způsobů reprezentace (resp. přesněji řečeno způsobu uložení) podmnožiny racionálních numerických hodnot (zkráceně čísel) v operační paměti počítače a/nebo v registrech jeho mikroprocesoru (CPU) či matematického koprocesoru (FPU). Jedná se o uložení vybrané množiny numerických hodnot v takzvaném systému pevné řádové (typicky binární nebo desetinné) tečky popř. naopak v systému plovoucí řádové tečky.

Poznámka: V tomto textu se ovšem budeme záměrně dopouštět drobného prohřešku oproti stávající normě českého jazyka, protože budeme neustále psát o řádové, desetinné a binární tečce a nikoli o čárce – z hlediska anglické terminologie to bude více konzistentní, i když z češtinářského hlediska by bylo zcela jistě korektnější psát o řádové čárce, protože se v češtině celá část čísla od části desetinné odděluje právě čárkou a nikoli tečkou, jak je tomu zvykem v anglosaských zemích (na druhou stranu programátoři, kterým je tento článek určen především, však tuto skutečnost zcela jistě znají).

V anglické literatuře se první zmíněná forma reprezentace číselných hodnot označuje zkratkou FX nebo FXP (tato zkratka je odvozena od fixed point), zatímco dnes častěji používaná reprezentace v systému plovoucí řádové tečky se všeobecně označuje zkratkou FP (odvozeno od floating point).

Poznámka: V jednom článku jsem mimochodem dokonce místo zkratky FX viděl i zkratku XP, ale to bylo před mnoha lety, ještě v době Windows 95 :-).

Nejprve si vysvětlíme princip obou metod použitých pro ukládání podmnožiny racionálních čísel a posléze si také řekneme, jaké výhody a nevýhody jednotlivé principy přináší v každodenní programátorské praxi a ve kterých situacích je vhodnější použít pevnou řádovou čárku. V dalším textu budeme formát pevné binární řádové tečky zkracovat na FX formát a formát používající plovoucí řádovou tečku budeme zapisovat jako FP formát.

11. Vybrané způsoby reprezentace numerických hodnot v operační paměti počítače

Při ukládání numerických hodnot do operační paměti počítače záhy narazíme na některé problémy, z nichž některé souvisí s konečným počtem bitů, které pro uložení dané hodnoty „obětujeme“ a další vycházejí ze způsobu zpracování hodnot mikroprocesorem či matematickým koprocesorem (což není případ Z80). V konečném počtu bitů je totiž možné uložit pouze konečné množství různých hodnot a je plně v rukou programátora, jak efektivně daný počet bitů využije či naopak promrhá ukládáním nepodstatných informací. Poměrně často se totiž stává, že i program využívající dvojitou či dokonce rozšířenou přesnost čísel při FP operacích (tj. datové typy double a extended/temporary) dává nesprávné výsledky dané nepochopením principu práce FP aritmetiky a přitom je možné se přesnějších výsledků dobrat i při použití pouhých 32 bitů, ale s pečlivě vyváženými aritmetickými a bitovými operacemi.

Na druhou stranu nejsou dnes používané mikroprocesory tak univerzálními zařízeními, jak by se na první pohled mohlo zdát. Mikroprocesory jsou totiž (většinou) navrženy tak, aby účinně, například v rámci jedné operace či instrukce, zpracovávaly pouze konstantní počet bitů. Příkladem mohou být dnes velmi rozšířené procesory řady x86, které jsou velmi dobré při práci s 32 bitovými hodnotami, ale při požadavku na aritmetické výpočty probíhající na (řekněme) 21 bitech se veškerá jejich efektivita ztrácí a procesor se širokými vnitřními sběrnicemi, matematickým koprocesorem atd. se potýká s prohazováním jednotlivých bitů.

Mnohem lepší situace nastane v případě, že se nějaká operace implementuje na programovatelném poli FPGA – zde je možné vytvořit obvody provádějící matematické a logické operace s libovolným počtem bitů, čímž se oproti univerzálním řešením (např. konstantní bitová šířka sběrnice a/nebo registrů) ušetří mnoho plochy těchto velmi zajímavých obvodů (FPGA mohou mimochodem znamenat i velkou šanci pro hnutí open source – pomocí nich by mohlo vznikat, a někde už vzniká open hardware, které by mohlo odstranit závislost na „uzavřených“ síťových a grafických kartách apod.).

Poznámka: mnohé FPGA však již mají své vlastní ALU a dokonce i násobičky, takže se z tohoto pohledu již nejedná o zcela univerzální obvody připravené pro jakékoli reprezentace numerických hodnot.

Vraťme se však ke způsobům reprezentace číselných hodnot v operační paměti. Nejprve předpokládejme, že pro reprezentaci vlastností určitého objektu či stavu z reálného světa použijeme N binárních číslic (bitů), tj. základních jednotek informace, která může nabývat pouze jedné ze dvou povolených hodnot (ty se značí například symboly yes/no nebo true/false, ale my se budeme spíše držet označení 0 a 1). Pomocí této uspořádané N-tice je možné popsat celkem:

2₀×2₁×2₂ … 2_N-1=2^N

jednoznačných, tj. navzájem odlišných, stavů. Množina těchto stavů může reprezentovat prakticky jakýkoliv abstraktní či reálný objekt. Přitom si musíme uvědomit, že u této množiny není implicitně řečeno ani myšleno, že se jedná například o celá kladná čísla, to je pouze jedna z mnoha možných interpretací zvolené N-tice (my programátoři máme tendenci považovat celá kladná čísla za přirozenou interpretaci bitové N-tice, to však vychází pouze z našeho pohledu na svět a z našich zkušeností). Reprezentaci momentálního stavu abstraktního či reálného objektu si můžeme představit jako zobrazení z množiny binárních stavů na elementy vzorové (a obecně neuspořádané) množiny. Nejčastěji používanými zobrazeními jsou zobrazení množiny binárních stavů na interval celých kladných čísel (Unsigned Integers), popřípadě na interval celých čísel (Signed Integers).

12. Uložení numerických hodnot ve formátu pevné řádové binární tečky

Numerické hodnoty zapsané ve formátu pevné řádové binární tečky se chápou jako podmnožina racionálních čísel, což jsou taková čísla, jejichž hodnoty je možné vyjádřit vztahem:

x_FX=a/b a,b leží v Z, b ≠ 0

Číselné hodnoty z uvažované podmnožiny jsou navíc omezeny podmínkou:

b=2^k b leží v Z, k leží v Z⁺

Protože b je celočíselnou mocninou dvojky (a ne desítky či jiného základu), určuje jeho hodnota n polohu binární tečky v uloženém čísle. Další podmínkou, která má však spíše implementační charakter, je zachování stejného počtu binárních cifer v každém reprezentovaném čísle, což mimo jiné znamená, že všechna čísla mají řádovou binární tečku umístěnou na stejném místě – z této podmínky ostatně plyne i název popisovaného způsobu reprezentace vybrané podmnožiny racionálních čísel. Tak jako i v jiných reprezentacích čísel, jsou nulové číslice před první nenulovou cifrou a za poslední nenulovou cifrou nevýznamné, proto je není zapotřebí uvádět.

Prakticky může být číselná hodnota v systému pevné řádové tečky uložena na osmi bitech například následujícím způsobem (uvažujeme pouze kladné hodnoty):

Pozice bitu	8	7	6	5	4	3	2	1
Váha bitu	2⁴	2³	2²	2¹	2⁰	2^-1	2^-2	2^-3
Desítková váha bitu	16	8	4	2	1	0,5	0,25	0,125

Poznámka: pochopitelně se jedná pouze o jednu konkrétní vybranou reprezentaci, protože je to programátor, který určuje, na kterém místě se řádová tečka nachází. Její pozice totiž není součástí vlastní hodnoty, ale je „zadrátována“ v algoritmech, které numerické hodnoty zpracovávají (součet, součin, CORDIC atd. atd.). Výběr pozice řádové tečky závisí především na tom, které hodnoty je zapotřebí reprezentovat a jaké ztráty přesnosti jsme ochotni akceptovat.

13. Přednosti a zápory formátu pevné řádové tečky

Ve výše uvedeném příkladu je binární řádová tečka umístěna vždy mezi třetím a čtvrtým bitem. Vzhledem k tomu, že je tato skutečnost dopředu známá algoritmu, který provádí zpracování čísel, není zapotřebí spolu s číslem uchovávat i pozici binární tečky, což výrazně snižuje počet bitů, které je zapotřebí rezervovat pro čísla ze zadaného rozsahu. To je tedy první přednost systému pevné řádové tečky – pokud programátor dopředu zná rozsah všech zpracovávaných hodnot a požadovanou přesnost, může být výhodné tento systém použít. Programátor také díky explicitním určení polohy řádové tečky může určit, ve kterém místě programu se musí přesnost či rozsah zvýšit a kdy naopak snížit. Lépe se tak využije počet bitů, které můžeme pro uložení jednoho čísla obětovat (typicky je tento počet bitů roven délce slova mikroprocesoru, popř. jeho celočíselnému násobku či naopak podílu).

Navíc je možné základní matematické operace (sčítání, odčítání, násobení a dělení) poměrně jednoduše implementovat i při použití formátu pevné řádové tečky. V případě, že není k dispozici specializovaný (a současně velmi komplikovaný) matematický koprocesor, je mnohdy mnohem jednodušší a rychlejší implementovat matematické operace v FX formátu. To je případ mnoha jednočipových mikroprocesorů (mikrořadičů), našeho oblíbeného čipu Zilog Z80, signálových procesorů, ale i specializovaných zařízení obsahujících programovatelné obvody CPLD či FPGA. Dnes sice mají komplikovanější (a dražší) FPGA implementovanou i jednotku FPU, ale mnohdy je výhodnější použít FPGA bez této jednotky a potřebné operace si do tohoto obvodu „vypálit“ po svém.

Třetí výhodou je fakt, že u FX formátu může programátor navrhnout a posléze také dodržet požadovanou přesnost všech prováděných výpočtů. To je velký rozdíl oproti FP formátu (resp. jeho podmnožinám, které se nejčastěji používají). Není vzácností narazit na programy, které používají datové typy float či double a přitom jsou výpočty prováděné v těchto programech zatíženy velkou chybou, protože si programátoři plně neuvědomují některé limity FP formátu. Kritické jsou například výpočty s peněžními hodnotami, ale i pouhé sčítání čísel, jež se od sebe o mnoho řádů liší, vede k velkým chybám, které dokonce mohou zapříčinit vznik nekonečných smyček, populární dělení nulou atd.

FX formát má však i některé nevýhody. První nevýhoda spočívá v tom, že tento formát není příliš podporován, a to ani po programové stránce (podpora v programovacích jazycích), ani výrobci mikroprocesorů pro počítače PC. Situace je však odlišná v oblasti jednočipových mikropočítačů, signálových procesorů (DSP), řídicích systémů, nebo například u IBM RS 6000, který kromě jednotky FPU obsahuje i FXU – jednotku pro provádění výpočtů v pevné řádové binární čárce. Na platformě x86 je možné pro FX formát použít instrukce MMX nebo jejich novější varinty (AVX atd.).

Dále může být použití FX formátu nevýhodné v případě, že se mají zpracovávat numerické hodnoty, které mají velkou dynamiku, tj. poměr mezi nejvyšší a nejnižší absolutní hodnotou. V takovém případě by se mohlo stát, že by se při použití FX formátu muselo pro každé číslo alokovat velké množství bitů, které by mohlo dokonce překročit počet bitů nutných pro FP formát. Také v případě, kdy dopředu nevíme, jaké hodnoty se budou zpracovávat, může být výhodnější použití FP formátu. Zde se však nabízí otázka, ve kterých případech nevíme, jaké hodnoty můžeme na vstupu získat: většinou je již z podstaty úlohy dopředu známé, s čím je možné počítat a které hodnoty jsou naprosto nesmyslné. Je však pravdou, že takovou analýzu málokdo dělá a když při výpočtech ve floatech dochází k chybám, tak se bez přemýšlení program přepíše na doubly a problém se tak buď odstraní, nebo alespoň odsune na pozdější dobu, například do chvíle, kdy jsou programu předložena reálná data a ne „pouze“ data testovací.

14. Uložení čísel ve formátu plovoucí řádové (binární) tečky

Uložení racionálních čísel ve formátu plovoucí řádové tečky (FP formát) se od FX formátu odlišuje především v tom, že si každá numerická hodnota sama v sobě nese polohu řádové tečky. Z tohoto důvodu je kromě bitů, které jsou rezervovány pro uložení významných číslic numerické hodnoty, nutné pro každou numerickou hodnotu rezervovat i další bity, pomocí nichž je určena mocnina o nějakém základu (typicky 2, 8, 10 či 16), kterou musí být významné číslice vynásobeny resp. vyděleny. První část čísla uloženého v FP formátu se nazývá mantisa, druhá část exponent. Obecný formát uložení a způsob získání původního čísla je následující:

x_FP=b^e×m

kde:

x_FX značí reprezentovanou numerickou hodnotu z podmnožiny reálných čísel
b je báze, někdy také nazývaná radix
e je hodnota exponentu (může být i záporná)
m je mantisa, která může být i záporná

Konkrétní formát numerických hodnot reprezentovaných v systému plovoucí řádové tečky závisí především na volbě báze (radixu) a také na počtu bitů rezervovaných pro uložení mantisy a exponentu. V minulosti existovalo mnoho různých formátů plovoucí řádové tečky (vzpomíná si někdo na Turbo Pascal s jeho šestibytovým datovým typem real?), dnes se však, ustálilo použití formátů specifikovaných v normě IEEE 754. Ovšem to není případ ZX Spectra, které má svůj vlastní formát, jenž si popíšeme v dalším textu.

15. Formát uložení FP hodnot na ZX Spectru

Při volbě konkrétního formátu uložení FP hodnot mají programátoři poměrně dosti volné ruce. Musí především zvolit:

Celkovou šířku slova s FP hodnotou
Zda bude mantisa a exponent uložena v binárním či BCD formátu (pro Z80 se BCD naprosto nehodí, na rozdíl od 6502)
Bitová šířka mantisy
Zda je první bit mantisy pevně nastaven na jedničku (a tudíž se nemusí ukládat)
Základ exponentu (typicky 2, 10 či 16)
Bitová šířka exponentu
Formát uložení, tj. kde bude uloženo znaménko, kde mantisa a kde exponent (FP hodnota je vlastně bitové pole)

Existuje mnoho formátů, z nichž nejzajímavější či nejpoužívanější vypadají následovně:

IBM 1130, IBM 1800 32 Bit single precision floating point
 
 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7
+-+---------------------------------------------+---------------+
|S|                mantissa                     |exp. with bias |
+-+---------------------------------------------+---------------+
 
 
GE-635 36 Bit single precision floating point
 
 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 0 1 2 3
+-+-------------+-+-----------------------------------------------------+
|S|  Two's exp. |S|            Two's complement mantissa                |
+-+-------------+-+-----------------------------------------------------+
 
 
Intel 8008, 8080 floating point UCRL-51940
 
 7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0
+-+-------------+-----------------------------------------------+
|S|  Two's exp. |                 positive mantissa             |
+-+-------------+-----------------------------------------------+
 
 
Altair BASIC 8080 floating point
 
 7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0
+---------------+-+---------------------------------------------+
|exp. with bias |S|       positive mantissa, MSB = 2^-1         |
+---------------+-+---------------------------------------------+
 
 
Z80 40 Bit floating point
 
 7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0
+-+-------------+-+-------------------------------------------------------------+
|S|  Two's exp. |S|            Two's complement mantissa, MSB = 2^1             |
+-+-------------+-+-------------------------------------------------------------+
 
 
IEEE 754 single precision
 
 7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0
+-+---------------+---------------------------------------------+
|S| exp. with bias|       positive mantissa, MSB = 2^-1         |
+-+---------------+---------------------------------------------+

Na ZX Spectru je použit 40bitový formát, přičemž 40 bitů bylo pravděpodobně zvoleno z toho důvodu, že všech pět univerzálních pracovních registrů má dohromady přesně tuto šířku (ale to může být jen spekulace):

 7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0
+-+-------------+-+-------------------------------------------------------------+
|exp. with bias |S|                       mantissa                              |
+-+-------------+-+-------------------------------------------------------------+

Poznámka: jedná se o formát používaný subrutinami v ROM a taktéž BASICem. Není však problém (je to pouze hodně pracné) si navrhnout formát vlastní.

Předpokládá se, že první bit mantisy je roven jedničce (což dává smysl), proto tento první bit není uložen a na jeho místě je znaménko mantisy. Exponent je posunutý o hodnotu 128 (viz další příklady).

Navíc tento formát obsahuje výjimku pro celočíselné hodnoty v rozsahu od –65535 až +65535. Tyto hodnoty jsou uloženy takovým způsobem, že první bajt (posunutý exponent) je nulový, druhý bajt obsahuje samé nuly pro kladná čísla a samé jedničky pro čísla záporná a teprve třetí a čtvrtý bajt obsahuje 16bitovou hodnotu bez znaménka. Poslední bajt je opět nulový. Tuto výjimku si podrobněji ukážeme příště.

16. Zásobník FP hodnot na ZX Spectru, subrutina pro tisk FP hodnot

V ROM ZX Spectra je uloženo několik subrutin určených pro zpracování FP hodnot. Z těchto subrutin nás dnes budou zajímat pouze dvě:

2DE3: THE 'PRINT A FLOATING-POINT NUMBER' SUBROUTINE
This subroutine prints x, the 'last value' on the calculator stack. The print format never occupies more than 14 spaces.
 
2AB1: THE 'STK-STORE' SUBROUTINE
This subroutine passes the values held in the A, B, C, D and E
A   First byte (when entering at STK_STO or STK_STORE)
B   Fifth byte
C   Fourth byte
D   Third byte
E   Second byte

Poznámka: dejte si pozor na druhou subrutinu, protože její ústřední část začíná až na adrese 0×2AB6 a nikoli na adrese 0×2AB1. Proto v demonstračním příkladu použijeme první adresu:

PRINT_FP      equ $2DE3
STK_STORE     equ $2AB6

Subrutina STK_STORE uloží FP hodnotu předanou ve všech pěti pracovních registrech (kromě HL) na zásobník (stack) používaný při FP výpočtech. Podrobnosti si řekneme příště, protože dnes nám postačuje vědět, jaké registry a v jakém pořadí jsou použity pro předání FP hodnoty:

        ; A  první bajt
        ; B  pátý byte
        ; C  čtvrtý byte
        ; D  třetí byte
        ; E  druhý bajt
        ld   A, ...
        ld   E, ...
        ld   D, ...
        ld   C, ...
        ld   B, ...
        call STK_STORE      ; uložit FP hodnotu na zásobník

Subrutina PRINT_FP přečte hodnotu z výše zmíněného zásobníku a vytiskne ji na obrazovku. Přitom se správně rozpoznají všechny speciální případy, tj. nuly, celočíselné hodnoty –65535..+65535 atd.

        call PRINT_FP       ; vytisknout FP hodnotu uloženou na vrcholu zásobníku
new_line:
        ld   A, 0x0d        ; kód znaku pro odřádkování
        rst  0x10           ; zavolání rutiny v ROM

Můžeme si tedy otestovat, jaké FP hodnoty jsou reprezentovány následujícími sekvencemi čtyřiceti bitů. Otestování bude snadné – pětici bajtů (40 bitů) uložíme do „FP zásobníku“ subrutinou STK_STORE a následně hodnotu vytiskneme zavoláním subrutiny PRINT_FP. Této subrutině se nepředávají žádné parametry – ty jsou na „FP zásobníku“:

        ld IX, fp0             ; adresa s pěticí bajtů FP hodnoty
        call print_fp_number   ; tisk FP hodnoty na obrazovku s odřádkováním

Tisknout budeme FP hodnoty reprezentované těmito sekvencemi bitů:

;         mantisa+128  s  exponent
fp0:    db %00000000, %00000000, %00000000, %00000000, %00000000
fp1:    db %10000000, %00000000, %00000000, %00000000, %00000000
fp2:    db %10000000, %10000000, %00000000, %00000000, %00000000
fp3:    db %10000000, %01000000, %00000000, %00000000, %00000000
fp4:    db %10000001, %01000000, %00000000, %00000000, %00000000
fp5:    db %10000001, %01000000, %00000000, %00000001, %00000000
fp6:    db %10000001, %00111111, %11111111, %11111111, %00000000

Výsledek by měl vypadat následovně:

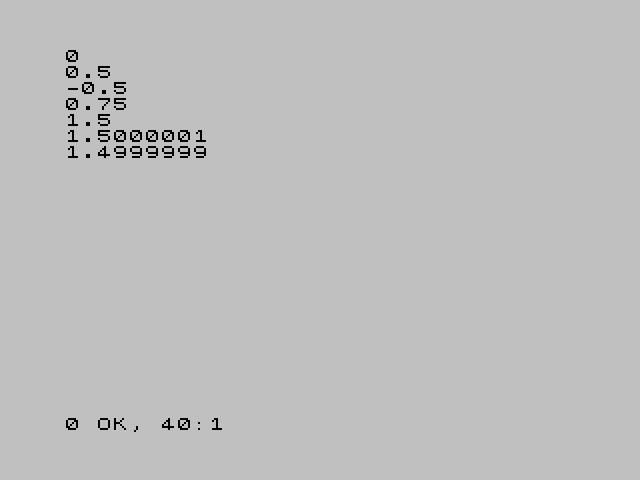
Obrázek 8: Sedm FP hodnot vypsaných na obrazovce ZX Spectra.

Proč hodnoty vypadají tak, jak vypadají:

První hodnota je 16bitovým číslem se znaménkem
Druhá hodnota obsahuje exponent=0 a mantisa má nastaven pouze nejvyšší bit za binární tečkou (ten se, jak víme, neukládá)
Třetí hodnota je totožná, jako hodnota druhá, ovšem je nastaven znaménkový bit
Čtvrtá hodnota obsahuje exponent=0 a mantisa je rovna 0.11 (binárně), tedy 0,5+0,25=0,75 dekadicky
Pátá hodnota má exponent=1 (×2) a mantisu stejnou, jako hodnota předchozí, tedy 2×0,75=1,5
Šestá hodnota je nepatrně vyšší, než hodnota pátá (viz v pořadí devátý bit zprava)
Sedmá hodnota je naopak nepatrně menší, než hodnota pátá

Pro tisk FP hodnoty je použita tato subrutina:

print_fp_number:
        ; A  první bajt
        ; B  pátý byte
        ; C  čtvrtý byte
        ; D  třetí byte
        ; E  druhý bajt
        ld   A, (IX)
        ld   E, (IX+1)
        ld   D, (IX+2)
        ld   C, (IX+3)
        ld   B, (IX+4)
        call STK_STORE      ; uložit FP hodnotu na zásobník
        call PRINT_FP       ; vytisknout FP hodnotu uloženou na vrcholu zásobníku
new_line:
        ld   A, 0x0d        ; kód znaku pro odřádkování
        rst  0x10           ; zavolání rutiny v ROM
        ret                 ; návrat ze subrutiny

17. Úplný zdrojový kód dnešního pátého demonstračního příkladu

Úplný zdrojový kód dnešního pátého a současně i posledního demonstračního příkladu je dostupný na adrese https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/83-print-fp-numbers.asm:

ENTRY_POINT   equ $8000
ROM_CLS       equ $0DAF
PRINT_FP      equ $2DE3
STK_STORE     equ $2AB6
 
 
        org ENTRY_POINT
 
start:
        call ROM_CLS           ; smazání obrazovky a otevření kanálu číslo 2 (screen)
 
        ld IX, fp0             ; adresa s pěticí bajtů FP hodnoty
        call print_fp_number   ; tisk FP hodnoty na obrazovku s odřádkováním
 
        ld IX, fp1             ; adresa s pěticí bajtů FP hodnoty
        call print_fp_number   ; tisk FP hodnoty na obrazovku s odřádkováním
 
        ld IX, fp2             ; adresa s pěticí bajtů FP hodnoty
        call print_fp_number   ; tisk FP hodnoty na obrazovku s odřádkováním
 
        ld IX, fp3             ; adresa s pěticí bajtů FP hodnoty
        call print_fp_number   ; tisk FP hodnoty na obrazovku s odřádkováním
 
        ld IX, fp4             ; adresa s pěticí bajtů FP hodnoty
        call print_fp_number   ; tisk FP hodnoty na obrazovku s odřádkováním
 
        ld IX, fp5             ; adresa s pěticí bajtů FP hodnoty
        call print_fp_number   ; tisk FP hodnoty na obrazovku s odřádkováním
 
        ld IX, fp6             ; adresa s pěticí bajtů FP hodnoty
        call print_fp_number   ; tisk FP hodnoty na obrazovku s odřádkováním
 
        ret
 
;         mantisa+128  s  exponent
fp0:    db %00000000, %00000000, %00000000, %00000000, %00000000
fp1:    db %10000000, %00000000, %00000000, %00000000, %00000000
fp2:    db %10000000, %10000000, %00000000, %00000000, %00000000
fp3:    db %10000000, %01000000, %00000000, %00000000, %00000000
fp4:    db %10000001, %01000000, %00000000, %00000000, %00000000
fp5:    db %10000001, %01000000, %00000000, %00000001, %00000000
fp6:    db %10000001, %00111111, %11111111, %11111111, %00000000
 
 
print_fp_number:
        ; A  první bajt
        ; B  pátý byte
        ; C  čtvrtý byte
        ; D  třetí byte
        ; E  druhý bajt
        ld   A, (IX)
        ld   E, (IX+1)
        ld   D, (IX+2)
        ld   C, (IX+3)
        ld   B, (IX+4)
        call STK_STORE      ; uložit FP hodnotu na zásobník
        call PRINT_FP       ; vytisknout FP hodnotu uloženou na vrcholu zásobníku
new_line:
        ld   A, 0x0d        ; kód znaku pro odřádkování
        rst  0x10           ; zavolání rutiny v ROM
        ret                 ; návrat ze subrutiny
 
 
end ENTRY_POINT

Překlad do assembleru:

ENTRY_POINT     EQU 8000
ROM_CLS         EQU 0DAF
PRINT_FP        EQU 2DE3
STK_STORE       EQU 2AB6
                ORG 8000
8000:           label start
8000:CDAF0D     CALL 0DAF
8003:DD213580   LD IX, 8035
8007:CD5880     CALL 8058
800A:DD213A80   LD IX, 803A
800E:CD5880     CALL 8058
8011:DD213F80   LD IX, 803F
8015:CD5880     CALL 8058
8018:DD214480   LD IX, 8044
801C:CD5880     CALL 8058
801F:DD214980   LD IX, 8049
8023:CD5880     CALL 8058
8026:DD214E80   LD IX, 804E
802A:CD5880     CALL 8058
802D:DD215380   LD IX, 8053
8031:CD5880     CALL 8058
8034:C9         RET
8035:           label fp0
8035:00000000   DEFB of 5 bytes
8039:00
803A:           label fp1
803A:80000000   DEFB of 5 bytes
803E:00
803F:           label fp2
803F:80800000   DEFB of 5 bytes
8043:00
8044:           label fp3
8044:80400000   DEFB of 5 bytes
8048:00
8049:           label fp4
8049:81400000   DEFB of 5 bytes
804D:00
804E:           label fp5
804E:81400001   DEFB of 5 bytes
8052:00
8053:           label fp6
8053:813FFFFF   DEFB of 5 bytes
8057:00
8058:           label print_fp_number
8058:DD7E00     LD A, (IX+00)
805B:DD5E01     LD E, (IX+01)
805E:DD5602     LD D, (IX+02)
8061:DD4E03     LD C, (IX+03)
8064:DD4604     LD B, (IX+04)
8067:CDB62A     CALL 2AB6
806A:CDE32D     CALL 2DE3
806D:           label new_line
806D:3E0D       LD A, 0D
806F:D7         RST 10
8070:C9         RET
8071:           END 8000
Emiting TAP basic loader
Emiting TAP from 8000 to 8070

18. Příloha: upravený soubor Makefile pro překlad demonstračních příkladů

Výše uvedené demonstrační příklady i příklady, které již byly popsány v předchozích devíti článcích [1] [2], [3], [4], [5], [6], [7], [8], [9], je možné přeložit s využitím souboru Makefile, jehož aktuální verze vypadá následovně (pro překlad a slinkování je použit assembler Pasmo):

ASSEMBLER := pasmo
 
all: 01.tap 02.tap 03.tap 04.tap 05.tap 06.tap 07.tap 08.tap 09.tap 10.tap \
    11.tap 12.tap 13.tap 14.tap 15.tap 16.tap 17.tap 18.tap 19.tap 20.tap \
    21.tap 22.tap 23.tap 24.tap 25.tap 26.tap 27.tap 28.tap 29.tap 30.tap \
    31.tap 32.tap 33.tap 34.tap 35.tap 36.tap 37.tap 38.tap 39.tap 40.tap \
    41.tap 42.tap 43.tap 44.tap 45.tap 46.tap 47.tap 48.tap 49.tap 50.tap \
    51.tap 52.tap 53.tap 54.tap 55.tap 56.tap 57.tap 58.tap 59.tap 60.tap \
    61.tap 62.tap 63.tap 64.tap 65.tap 66.tap 67.tap 68.tap 69.tap 70.tap \
    71.tap 72.tap 73.tap 74.tap 75.tap 76.tap 77.tap 78.tap 79.tap 80.tap \
    81.tap 82.tap 83.tap
 
clean:
        rm -f *.tap
 
.PHONY: all clean
 
 
01.tap: 01-color-attribute.asm
        $(ASSEMBLER) -v -d --tap $< $@ > 01-color-attribute.lst
 
02.tap: 02-blinking-attribute.asm
        $(ASSEMBLER) -v -d --tap $< $@ > 02-blinking-attribute.lst
 
03.tap: 03-symbolic-names.asm
        $(ASSEMBLER) -v -d --tap $< $@ > 03-symbolic-names.lst
 
04.tap: 04-operators.asm
        $(ASSEMBLER) -v -d --tap $< $@ > 04-operators.lst
 
05.tap: 05-better-symbols.asm
        $(ASSEMBLER) -v -d --tap $< $@ > 05-better-symbols.lst
 
06.tap: 06-tapbas-v1.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 06-tapbas-v1.lst
 
07.tap: 07-tapbas-v2.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 07-tapbas-v2.lst
 
08.tap: 08-loop.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 08-loop.lst
 
09.tap: 09-loop.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 09-loop.lst
 
10.tap: 10-loop.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 10-loop.lst
 
11.tap: 11-loop.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 11-loop.lst
 
12.tap: 12-loop.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 12-loop.lst
 
13.tap: 13-loop.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 13-loop.lst
 
14.tap: 14-loop.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 14-loop.lst
 
15.tap: 15-loop.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 15-loop.lst
 
16.tap: 16-loop.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 16-loop.lst
 
17.tap: 17-loop.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 17-loop.lst
 
18.tap: 18-cls.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 18-cls.lst
 
19.tap: 19-print-char-call.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 19-print-char-call.lst
 
20.tap: 20-print-char-rst.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 20-print-char-rst.lst
 
21.tap: 21-print-char.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 21-print-char.lst
 
22.tap: 22-print-all-chars.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 22-print-all-chars.lst
 
23.tap: 23-print-all-chars.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 23-print-all-chars.lst
 
24.tap: 24-change-color.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 24-change-color.lst
 
25.tap: 25-change-flash.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 25-change-flash.lst
 
26.tap: 26-print-at.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 26-print-at.lst
 
27.tap: 27-print-string.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 27-print-string.lst
 
28.tap: 28-print-string.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 28-print-string.lst
 
29.tap: 29-print-colorized-string.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 29-print-colorized-string.lst
 
30.tap: 30-print-string-ROM.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 30-print-string-ROM.lst
 
31.tap: 31-attributes.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 31-attributes.lst
 
32.tap: 32-fill-in-vram.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 32-fill-in-vram.lst
 
33.tap: 33-fill-in-vram-no-ret.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 33-fill-in-vram-no-ret.lst
 
34.tap: 34-fill-in-vram-pattern.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 34-fill-in-vram-pattern.lst
 
35.tap: 35-slow-fill-in-vram.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 35-slow-fill-in-vram.lst
 
36.tap: 36-slow-fill-in-vram-no-ret.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 36-slow-fill-in-vram-no-ret.lst
 
37.tap: 37-fill-block.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 37-fill-block.lst
 
38.tap: 38-fill-block-with-pattern.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 38-fill-block-with-pattern.lst
 
39.tap: 39-fill-block-optimized.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 39-fill-block-optimized.lst
 
40.tap: 40-draw-char.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 40-draw-char.lst
 
41.tap: 41-draw-any-char.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 41-draw-any-char.lst
 
42.tap: 42-block-anywhere.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 42-block-anywhere.lst
 
43.tap: 43-block-anywhere-rrca.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 43-block-anywhere-rrca.lst
 
44.tap: 44-better-draw-char.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 44-better-draw-char.lst
 
45.tap: 45-even-better-draw-char.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 45-even-better-draw-char.lst
 
46.tap: 46-draw-char-at.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 46-draw-char-at.lst
 
47.tap: 47-draw-char-at-unrolled.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 47-draw-char-at-unrolled.lst
 
48.tap: 48-incorrect-print-string.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 48-incorrect-print-string.lst
 
49.tap: 49-correct-print-string.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 49-correct-print-string.lst
 
50.tap: 50-ascii-table.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 50-ascii-table.lst
 
51.tap: 51-plot-block.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 51-plot-block.lst
 
52.tap: 52-plot-pixel.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 52-plot-pixel.lst
 
53.tap: 53-plot-pixel.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 53-plot-pixel.lst
 
54.tap: 54-plot-pixel-on-background.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 54-plot-pixel-on-background.lst
 
55.tap: 55-plot-pixel-on-background.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 55-plot-pixel-on-background.lst
 
56.tap: 56-inverse-ascii-table.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 56-inverse-ascii-table.lst
 
57.tap: 57-plot-pixel-on-inverse-background.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 57-plot-pixel-on-inverse-background.lst
 
58.tap: 58-plot-inverse-pixel-on-inverse-background.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 58-plot-inverse-pixel-on-inverse-background.lst
 
59.tap: 59-configurable-ascii-table.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 59-configurable-ascii-table.lst
 
60.tap: 60-plot-over.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 60-plot-over.lst
 
61.tap: 61-print-number-A.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 61-print-number-A.lst
 
62.tap: 62-print-number-B.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 62-print-number-B.lst
 
63.tap: 63-print-number-C.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 63-print-number-C.lst
 
64.tap: 64-print-number-D.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 64-print-number-D.lst
 
65.tap: 65-more-numbers-A.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 65-more-numbers-A.lst
 
66.tap: 66-more-numbers-B.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 66-more-numbers-B.lst
 
67.tap: 67-print-flags-1.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 67-print-flags-1.lst
 
68.tap: 68-print-flags-2.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 68-print-flags-2.lst
 
69.tap: 69-print-flags-3.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 69-print-flags-3.lst
 
70.tap: 70-print-flags-4.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 70-print-flags-4.lst
 
71.tap: 71-print-flags-5.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 71-print-flags-5.lst
 
72.tap: 72-print-flags-6.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 72-print-flags-6.lst
 
73.tap: 73-print-flags-7.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 73-print-flags-7.lst
 
74.tap: 74-print-hex-number.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 74-print-hex-number.lst
 
75.tap: 75-print-hex-number.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 75-print-hex-number.lst
 
76.tap: 76-print-hex-numbers.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 76-print-hex-numbers.lst
 
77.tap: 77-add-hex-numbers.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 77-add-hex-numbers.lst
 
78.tap: 78-add-bcd-numbers.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 78-add-bcd-numbers.lst
 
79.tap: 79-print-hex-digit-jmp.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 79-print-hex-digit-jmp.lst
 
80.tap: 80-print-hex-digit-overflow.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 80-print-hex-digit-overflow.lst
 
81.tap: 81-print-hex-digit-daa.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 81-print-hex-digit-daa.lst
 
82.tap: 82-print-hex-numbers-daa.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 82-print-hex-numbers-daa.lst
 
83.tap: 83-print-fp-numbers.asm
        $(ASSEMBLER) -v -d --tapbas $< $@ > 83-print-fp-numbers.lst

19. Repositář s demonstračními příklady

V tabulce zobrazené pod tímto odstavcem jsou uvedeny odkazy na všechny prozatím popsané demonstrační příklady určené pro překlad a spuštění na osmibitovém domácím mikropočítači ZX Spectrum (libovolný model či jeho klon), které jsou psány v assembleru mikroprocesoru Zilog Z80. Pro překlad těchto demonstračních příkladů je možné použít například assembler Pasmo (viz též úvodní článek):

#	Soubor	Stručný popis	Adresa
1	01-color-attribute.asm	modifikace jednoho barvového atributu	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/01-color-attribute.asm
2	02-blinking-attribute.asm	barvový atribut s nastavením bitů pro blikání a vyšší intenzitu	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/02-blinking-attribute.asm
3	03-symbolic-names.asm	symbolická jména v assembleru	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/03-symbolic-names.asm
4	04-operators.asm	operátory a operace se symbolickými hodnotami	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/04-operators.asm
5	05-better-symbols.asm	tradičnější symbolická jména	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/05-better-symbols.asm
6	06-tapbas-v1.asm	vygenerování BASICovského loaderu (neúplný příklad)	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/06-tapbas-v1.asm
7	07-tapbas-v2.asm	vygenerování BASICovského loaderu (úplný příklad)	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/07-tapbas-v2.asm
8	08-loop.asm	jednoduchá počítaná programová smyčka: naivní varianta	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/08-loop.asm
9	09-loop.asm	programová smyčka: zkrácení kódu pro vynulování použitých pracovních registrů	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/09-loop.asm
10	10-loop.asm	programová smyčka: optimalizace skoku na konci smyčky (instrukce DJNZ)	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/10-loop.asm
11	11-loop.asm	programová smyčka: optimalizace využití pracovních registrů	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/11-loop.asm
12	12-loop.asm	programová smyčka: použití pracovního registru IX	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/12-loop.asm
13	13-loop.asm	programová smyčka: použití pracovního registru IY	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/13-loop.asm
14	14-loop.asm	programová smyčka se šestnáctibitovým počitadlem, základní varianta	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/14-loop.asm
15	15-loop.asm	programová smyčka se šestnáctibitovým počitadlem, vylepšená varianta	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/15-loop.asm
16	16-loop.asm	použití relativního skoku a nikoli skoku absolutního	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/16-loop.asm
17	17-loop.asm	programová smyčka: inc l namísto inc hl	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/17-loop.asm

18	18-cls.asm	smazání obrazovky a otevření kanálu číslo 2 (screen) přes funkci v ROM	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/18-cls.asm
19	19-print-char-call.asm	smazání obrazovky a výpis jednoho znaku na obrazovku přes funkci v ROM (použití instrukce CALL)	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/19-print-char-call.asm
20	20-print-char-rst.asm	smazání obrazovky a výpis jednoho znaku na obrazovku přes funkci v ROM (použití instrukce RST)	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/20-print-char-rst.asm
21	21-print-char.asm	pouze výpis jednoho znaku na obrazovku bez jejího smazání	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/21-print-char.asm
22	22-print-all-chars.asm	výpis znakové sady znak po znaku (nekorektní verze příkladu)	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/22-print-all-chars.asm
23	23-print-all-chars.asm	výpis znakové sady znak po znaku (korektní verze příkladu)	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/23-print-all-chars.asm
24	24-change-color.asm	změna barvových atributů (popředí a pozadí) vypisovaných znaků	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/24-change-color.asm
25	25-change-flash.asm	povolení či zákaz blikání vypisovaných znaků	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/25-change-flash.asm
26	26-print-at.asm	výpis znaku či znaků na určené místo na obrazovce	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/26-print-at.asm
27	27-print-string.asm	výpis celého řetězce explicitně zapsanou programovou smyčkou (základní varianta)	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/27-print-string.asm
28	28-print-string.asm	výpis celého řetězce explicitně zapsanou programovou smyčkou (vylepšená varianta)	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/28-print-string.asm
29	29-print-colorized-string.asm	výpis řetězce, který obsahuje i řídicí znaky pro změnu barvy atd.	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/29-print-colorized-string.asm
30	30-print-string-ROM.asm	výpis řetězce s využitím služby/subrutiny uložené v ROM ZX Spectra	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/30-print-string-ROM.asm

31	31-attributes.asm	modifikace atributů pro tisk řetězce subrutinou uloženou v ROM	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/31-attributes.asm
32	32-fill-in-vram.asm	vyplnění celé bitmapy barvou popředí, návrat do systému	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/32-fill-in-vram.asm
33	33-fill-in-vram-no-ret.asm	vyplnění celé bitmapy barvou popředí, bez návratu do systému	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/33-fill-in-vram-no-ret.asm
34	34-fill-in-vram-pattern.asm	vyplnění celé bitmapy zvoleným vzorkem	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/34-fill-in-vram-pattern.asm
35	35-slow-fill-in-vram.asm	pomalé vyplnění celé bitmapy, vizualizace struktury bitmapy	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/35-slow-fill-in-vram.asm
36	36-slow-fill-in-vram-no-ret.asm	pomalé vyplnění celé bitmapy, vizualizace struktury bitmapy, bez návratu do systému	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/36-slow-fill-in-vram-no-ret.asm
37	37-fill-block.asm	vykreslení bloku 8×8 pixelů	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/37-fill-block.asm
38	38-fill-block-with-pattern.asm	vykreslení bloku 8×8 pixelů zvoleným vzorkem	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/38-fill-block-with-pattern.asm
39	39-fill-block-optimized.asm	optimalizace předchozího příkladu	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/39-fill-block-optimized.asm
40	40-draw-char.asm	vykreslení znaku do levého horního rohu	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/40-draw-char.asm
41	41-draw-any-char.asm	podprogram pro vykreslení libovolně zvoleného znaku do levého horního rohu	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/41-draw-any-char.asm
42	42-block-anywhere.asm	podprogramy pro vykreslení bloku 8×8 pixelů kamkoli na obrazovku	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/42-block-anywhere.asm

43	43-block-anywhere-rrca.asm	podprogramy pro vykreslení bloku 8×8 pixelů kamkoli na obrazovku, vylepšená varianta	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/43-block-anywhere-rrca.asm
44	44-better-draw-char.asm	vykreslení znaku v masce 8×8 pixelů, vylepšená varianta	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/44-better-draw-char.asm
45	45-even-better-draw-char.asm	posun offsetu pro vykreslení dalšího znaku	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/45-even-better-draw-char.asm
46	46-draw-char-at.asm	vykreslení znaku v masce 8×8 pixelů kamkoli na obrazovku	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/46-draw-char-at.asm
47	47-draw-char-at-unrolled.asm	vykreslení znaku v masce 8×8 pixelů kamkoli na obrazovku	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/47-draw-char-at-unrolled.asm
48	48-incorrect-print-string.asm	tisk řetězce, nekorektní varianta	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/48-incorrect-print-string.asm
49	49-correct-print-string.asm	tisk řetězce, korektní varianta	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/49-correct-print-string.asm

50	50-ascii-table.asm	tisk několika bloků ASCII tabulky	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/50-ascii-table.asm
51	51-plot-block.asm	vykreslení pixelu verze 1: zápis celého bajtu na pozici pixelu	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/51-plot-block.asm
52	52-plot-pixel.asm	vykreslení pixelu verze 2: korektní vykreslení jednoho pixelu, ovšem překreslení celého bajtu	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/52-plot-pixel.asm
53	53-plot-pixel.asm	vykreslení pixelu verze 3: vylepšená verze předchozího demonstračního příkladu	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/53-plot-pixel.asm
54	54-plot-pixel-on-background.asm	vykreslení pixelu vůči pozadí (nekorektní varianta)	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/54-plot-pixel-on-background.asm
55	55-plot-pixel-on-background.asm	vykreslení pixelu vůči pozadí (korektní varianta)	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/55-plot-pixel-on-background.asm

56	56-inverse-ascii-table.asm	vykreslení ASCII tabulky inverzní barvou (inkoust vs. papír)	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/56-inverse-ascii-table.asm
57	57-plot-pixel-on-inverse-background.asm	vykreslení pixelů barvou papíru proti inverzní ASCII tabulce	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/57-plot-pixel-on-inverse-background.asm
58	58-plot-inverse-pixel-on-inverse-background.asm	vykreslení pixelů inverzní barvou proti inverzní ASCII tabulce	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm58-plot-inverse-pixel-on-inverse-background.asm/
59	59-configurable-ascii-table.asm	vykreslení ASCII tabulky buď přímo inkoustem nebo inverzně	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/59-configurable-ascii-table.asm
60	60-plot-over.asm	přibližná implementace příkazu PLOT OVER	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/60-plot-over.asm

61	61-print-number-A.asm	ukázka použití podprogramu pro tisk celého čísla	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/61-print-number-A.asm
62	62-print-number-B.asm	pokus o vytištění záporných čísel	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/62-print-number-B.asm
63	63-print-number-C.asm	tisk maximální podporované hodnoty 9999	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/63-print-number-C.asm
64	64-print-number-D.asm	tisk vyšší než podporované hodnoty 10000	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/64-print-number-D.asm
65	65-more-numbers-A.asm	vytištění číselné řady	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/65-more-numbers-A.asm
66	66-more-numbers-B.asm	kombinace tisku celočíselných hodnot s dalšími subrutinami	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/66-more-numbers-B.asm
67	67-print-flags-1.asm	příznakové bity po provedení celočíselné operace 1+2	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/67-print-flags-1.asm
68	68-print-flags-2.asm	příznakové bity po provedení celočíselné operace 0+0	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/68-print-flags-2.asm
69	69-print-flags-3.asm	příznakové bity po provedení operace 255+1	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/69-print-flags-3.asm
70	70-print-flags-4.asm	příznakové bity po provedení operace 254+1	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/70-print-flags-4.asm
71	71-print-flags-5.asm	příznakové bity po provedení operace 255+255	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/71-print-flags-5.asm
72	72-print-flags-6.asm	výsledek operace 100+100, nastavení příznakových bitů	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/72-print-flags-6.asm
73	73-print-flags-7.asm	výsledek operace 128+128, nastavení příznakových bitů	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/73-print-flags-7.asm

74	74-print-hex-number.asm	tisk hexadecimálního čísla v rozsahu 0×00 až 0×ff (neoptimalizovaná varianta)	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/74-print-hex-number.asm
75	75-print-hex-number.asm	tisk hexadecimálního čísla v rozsahu 0×00 až 0×ff (optimalizovaná varianta)	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/75-print-hex-number.asm
76	76-print-hex-numbers.asm	tisk několika hexadecimálních hodnot	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/76-print-hex-numbers.asm
77	77-add-hex-numbers.asm	součet dvou osmibitových hexadecimálních hodnot s tiskem všech výsledků	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/77-add-hex-numbers.asm
78	78-add-bcd-numbers.asm	součet dvou osmibitových BCD hodnot s tiskem všech výsledků	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/78-add-bcd-numbers.asm

79	79-print-hex-digit-jmp.asm	tisk jedné hexadecimální cifry s využitím podmíněného skoku	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/79-print-hex-digit-jmp.asm
80	80-print-hex-digit-overflow.asm	otestování, jaký znak je vytištěn pro hodnoty větší než 15	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/80-print-hex-digit-overflow.asm
81	81-print-hex-digit-daa.asm	tisk jedné hexadecimální cifry s využitím instrukce DAA	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/81-print-hex-digit-daa.asm
82	82-print-hex-numbers-daa.asm	tisk série hexadecimálních hodnot s využitím instrukce DAA	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/82-print-hex-numbers-daa.asm
83	83-print-fp-numbers.asm	tisk numerických hodnot reprezentovaných v systému plovoucí řádové tečky	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/83-print-fp-numbers.asm

84	Makefile	Makefile pro překlad a slinkování všech demonstračních příkladů do podoby obrazu magnetické pásky	https://github.com/tisnik/8bit-fame/blob/master/Speccy-asm/Makefile

20. Odkazy na Internetu

z80 standalone assembler
https://www.asm80.com/onepage/asmz80.html
The ZX BASIC Compiler
https://www.boriel.com/pages/the-zx-basic-compiler.html
Z80 Assembly programming for the ZX Spectrum
https://www.chibiakumas.com/z80/ZXSpectrum.php
8-BIT SMACKDOWN! 65C02 vs. Z80: slithy VLOGS #6
https://www.youtube.com/watch?v=P1paVoFEvyc
Instrukce mikroprocesoru Z80
https://clrhome.org/table/
Z80 instructions: adresní režimy atd.
https://jnz.dk/z80/instructions.html
Z80 Instruction Groups
https://jnz.dk/z80/instgroups.html
Elena, New programming language for the ZX Spectrum Next
https://vintageisthenewold.com/elena-new-programming-language-for-the-zx-spectrum-next/
Sinclair BASIC
https://worldofspectrum.net/legacy-info/sinclair-basic/
Grafika na osmibitových počítačích firmy Sinclair
https://www.root.cz/clanky/grafika-na-osmibitovych-pocitacich-firmy-sinclair/
Grafika na osmibitových počítačích firmy Sinclair II
https://www.root.cz/clanky/grafika-na-osmibitovych-pocitacich-firmy-sinclair-ii/
HiSoft BASIC
https://worldofspectrum.net/infoseekid.cgi?id=0008249
YS MegaBasic
https://worldofspectrum.net/infoseekid.cgi?id=0008997
Beta Basic
https://worldofspectrum.net/infoseekid.cgi?id=0007956
BASIC+
https://worldofspectrum.net/infoseekid.php?id=0014277
Spectrum ROM Memory Map
https://skoolkit.ca/disassemblies/rom/maps/all.html
Goto subroutine
https://skoolkit.ca/disassemblies/rom/asm/7783.html
Spectrum Next: The Evolution of the Speccy
https://www.specnext.com/about/
Sedmdesátiny assemblerů: lidsky čitelný strojový kód
https://www.root.cz/clanky/sedmdesatiny-assembleru-lidsky-citelny-strojovy-kod/
Programovací jazyk BASIC na osmibitových mikropočítačích
https://www.root.cz/clanky/programovaci-jazyk-basic-na-osmibitovych-mikropocitacich/
Programovací jazyk BASIC na osmibitových mikropočítačích (2)
https://www.root.cz/clanky/programovaci-jazyk-basic-na-osmibitovych-mikropocitacich-2/#k06
Programovací jazyk BASIC na osmibitových mikropočítačích (3)
https://www.root.cz/clanky/programovaci-jazyk-basic-na-osmibitovych-mikropocitacich-3/
Sinclair BASIC (Wikipedia CZ)
http://cs.wikipedia.org/wiki/Sinclair_BASIC
Assembly Language: Still Relevant Today
http://wilsonminesco.com/AssyDefense/
Programovani v assembleru na OS Linux
http://www.cs.vsb.cz/grygarek/asm/asmlinux.html
Why Assembly Language Programming? (Why Learning Assembly Language Is Still a Good Idea)
https://wdc65×x.com/markets/education/why-assembly-language-programming/
Low Fat Computing
http://www.ultratechnology.com/lowfat.htm
Assembly Language
https://www.cleverism.com/skills-and-tools/assembly-language/
Why do we need assembly language?
https://cs.stackexchange.com/questions/13287/why-do-we-need-assembly-language
Assembly language (Wikipedia)
https://en.wikipedia.org/wiki/Assembly_language#Historical_perspective
Assembly languages
https://curlie.org/Computers/Programming/Languages/Assembly/
vasm
http://sun.hasenbraten.de/vasm/
B-ELITE
https://jsj.itch.io/b-elite
ZX-Spectrum Child
http://www.dotkam.com/2008/11/19/zx-spectrum-child/
Speccy.cz
http://www.speccy.cz/
Planet Sinclair
http://www.nvg.ntnu.no/sinclair/
World of Spectrum
http://www.worldofspectrum.org/
The system variables
https://worldofspectrum.org/ZXBasicManual/zxmanchap25.html
ZX Spectrum manual: chapter #17 Graphics
https://worldofspectrum.org/ZXBasicManual/zxmanchap17.html
Why does Sinclair BASIC have two formats for storing numbers in the same structure?
https://retrocomputing.stackexchange.com/questions/8834/why-does-sinclair-basic-have-two-formats-for-storing-numbers-in-the-same-structu
Plovoucí řádová čárka na ZX Spectru
https://www.root.cz/clanky/norma-ieee-754-a-pribuzni-formaty-plovouci-radove-tecky/#k05
Norma IEEE 754 a příbuzní: formáty plovoucí řádové tečky
https://www.root.cz/clanky/norma-ieee-754-a-pribuzni-formaty-plovouci-radove-tecky/#k05
1A1B: THE ‚REPORT AND LINE NUMBER PRINTING‘ SUBROUTINE
https://skoolkid.github.io/rom/asm/1A1B.html
2DE3: THE ‚PRINT A FLOATING-POINT NUMBER‘ SUBROUTINE
https://skoolkid.github.io/rom/asm/2DE3.html
5C63: STKBOT – Address of bottom of calculator stack
https://skoolkid.github.io/rom/asm/5C63.html
5C65: STKEND – Address of start of spare space
https://skoolkid.github.io/rom/asm/5C65.html
Why does Sinclair BASIC have two formats for storing numbers in the same structure?
https://retrocomputing.stackexchange.com/questions/8834/why-does-sinclair-basic-have-two-formats-for-storing-numbers-in-the-same-structu
Chapter 24: The memory
https://worldofspectrum.org/ZXBasicManual/zxmanchap24.html
Survey of Floating-Point Formats
https://mrob.com/pub/math/floatformats.html
Convert an 8bit number to hex in z80 assembler
https://stackoverflow.com/questions/22838444/convert-an-8bit-number-to-hex-in-z80-assembler
80 MICROPROCESSOR Instruction Set Summary
http://www.textfiles.com/programming/CARDS/z80
Extended Binary Coded Decimal Interchange Code
http://en.wikipedia.org/wiki/EBCDIC
ASCII/EBCDIC Conversion Table
http://docs.hp.com/en/32212–90008/apcs01.html
EBCDIC
http://www.hansenb.pdx.edu/DMKB/dict/tutorials/ebcdic.php
EBCDIC tables
http://home.mnet-online.de/wzwz.de/temp/ebcdic/cc_en.htm
The Mainframe Blog
http://mainframe.typepad.com/blog/2006/11/my_personal_mai.html
Binary-coded decimal
https://en.wikipedia.org/wiki/Binary-coded_decimal
BCD
https://cs.wikipedia.org/wiki/BCD
Z80 heaven: Floating Point
http://z80-heaven.wikidot.com/floating-point
Z80, the 8-bit Number Cruncher
http://www.andreadrian.de/oldcpu/Z80_number_cruncher.html
Floating-point library for Z80
https://github.com/DW0RKiN/Floating-point-Library-for-Z80
z80float
https://github.com/Zeda/z80float
ZX Spectrum BASIC Programming – 2nd Edition
https://archive.org/details/zx-spectrum-basic-programming/page/n167/mode/2up
ZX Spectrum BASIC Programming – 2nd Edition
https://archive.org/details/zx-spectrum-basic-programming/page/n169/mode/2up

Seriál: Vývoj pro slavné ZX Spectrum

Aritmetické operace s hodnotami uloženými binárně i ve formátu BCD
Tisk hexadecimálních hodnot s využitím instrukce DAA na ZX Spectru
Kopie datových bloků na ZX Spectru: přenášení bajt po bajtu

Přečtěte si všechny díly seriálu Vývoj pro slavné ZX Spectrum nebo sledujte jeho RSS

Vstoupit do diskuse (13 názorů)

Pavel Tišnovský

Vystudoval VUT FIT a v současné době pracuje na projektech vytvářených v jazycích Python a Go.

Témata:

Assembler

jj je to tak. Desny je, ze jsem to vedel a uspesne zapomel :/ Fakt je, ze devitimistny MSFLOAT byval dlouho vsude mozne, i v ruznych formatech a tak. Mea culpa

Pavel Tišnovský

Zlatý podporovatel

Sdílet

Obsah

1. Tisk hexadecimálních hodnot podruhé

2. Úplný zdrojový kód dnešního prvního demonstračního příkladu

3. Malá odbočka: přetečení hodnoty cifry

4. Úplný zdrojový kód dnešního druhého demonstračního příkladu

5. Využití instrukce DAA namísto podmíněného skoku

6. Podrobný popis operací prováděných při převodu hexadecimální cifry na ASCII znak

7. Úplný zdrojový kód dnešního třetího demonstračního příkladu

8. Vylepšené vytištění osmibitové hexadecimální hodnoty

9. Úplný zdrojový kód dnešního čtvrtého demonstračního příkladu

10. Reprezentace numerických hodnot ve formátu pevné a plovoucí řádové (binární) tečky

11. Vybrané způsoby reprezentace numerických hodnot v operační paměti počítače

12. Uložení numerických hodnot ve formátu pevné řádové binární tečky

13. Přednosti a zápory formátu pevné řádové tečky

14. Uložení čísel ve formátu plovoucí řádové (binární) tečky

15. Formát uložení FP hodnot na ZX Spectru

16. Zásobník FP hodnot na ZX Spectru, subrutina pro tisk FP hodnot

17. Úplný zdrojový kód dnešního pátého demonstračního příkladu

18. Příloha: upravený soubor Makefile pro překlad demonstračních příkladů

19. Repositář s demonstračními příklady

20. Odkazy na Internetu

Aritmetické operace s hodnotami uloženými binárně i ve formátu BCD