Obsah
1. Příkazy pro změnu tloušťky a délky vytvářených větví
2. Praktické příklady změny tloušťky a délky větví
3. Příkazy určené pro změnu barvy, kterou želva kreslí
4. Praktické příklady změny barvy
5. Orientace v prostoru – nakreslení souřadných os
6. Vytváření 3D modelů stromů
7. Demonstrační příklad – interaktivní prohlížení souborů typu RAW
8. Screenshoty trojrozměrných modelů L-systémů zobrazených v demonstračním příkladu
9. Obsah dalšího pokračování tohoto seriálu
1. Příkazy pro změnu tloušťky a délky vytvářených větví
V předchozí části tohoto seriálu jsme si ukázali praktické použití několika základních příkazů vyskytujících se v přepisovacích pravidlech, pomocí nichž může želva v programu Lparser vykreslovat útvary nazývané podle svého tvaru „větve“ a „listy“. Také víme, že „větve“ jsou většinou tvořeny relativně úzkými a dlouhými objekty, například válci, podlouhlými elipsoidy nebo čtveřicí úzkých a dlouhých obdélníků tvořících protáhlý hranol. Konkrétní geometrický tvar závisí zejména na volbě výstupního formátu. Například program POV-Ray pracuje s elipsoidy (v podstatě se jedná o koule, které mají v každé ose nastavené jiné měřítko) a implicitními plochami; zatímco v souborech typu RAW se mohou vyskytovat pouze trojúhelníky.
Naproti tomu „listy“, jejichž vrcholy jsou specifikovány neviditelnými značkami, které želva na základě explicitně zadaných příkazů klade do trojrozměrného prostoru při svém pohybu, jsou ve výsledném modelu vytvářeny pomocí plošných polygonů, především trojúhelníků. Je to z toho důvodu, že pouze u trojúhelníků je zaručeno, že tvoří vždy rovinný útvar (v případě listů se trojúhelníky exportují i pro program POV-Ray). V této kapitole se budeme věnovat způsobu, jakým je možné změnit tloušťku a délku vytvářených větví, protože mnoho reálných rovinných i prostorových modelů má délku větví proměnnou.
Minule jsme si také řekli, že ucelené definice plošných (2D) i trojrozměrných (3D) L-systémů určených pro zpracování v programu Lparser, jsou uloženy v textových neboli ASCII souborech s koncovkou „.ls“. V těchto souborech jsou zapsány počáteční parametry L-systému, axiom (přepisovaný řetězec) a sada přepisovacích pravidel. Na prvních třech významových řádcích, tj. řádcích, které neobsahují jen poznámku či pouze bílé znaky, se vyskytují tři důležité číselné hodnoty, které ovlivňují globální tvar výsledného trojrozměrného modelu a jejichž průběžnou změnou je možné systémy animovat (to si podrobněji ukážeme v příští části tohoto seriálu). Jedná se o následující hodnoty:
- hloubka rekurze: celkový počet aplikací přepisovacích pravidel na axiom; tímto parametrem se ovlivňuje počet vygenerovaných entit a tím i složitost celého objektu
- implicitní úhel: úhel, o který se natáčí želva při rotaci okolo některé ze souřadných os, tj. vektorů Forward (F), Up (U) či Left (L)
- tloušťka větví: tloušťka je zadaná v procentech délky větví, typická hodnota se pohybuje v rozsahu 5–30% (znak procenta se však nezadává, pouze číselná hodnota)
V přepisovacích pravidlech se může objevit několik symbolů, které mění délku i tloušťku větví. Mezi příkazy ovlivňující délku větví patří zejména:
| Symbol | Význam symbolu |
|---|---|
| " | zvýšení faktoru délky větví o hodnotu 1,1 (vynásobení délky touto hodnotou) |
| ' | snížení faktoru délky větví o hodnotu 0,9 (vynásobení délky touto hodnotou) |
| "(x) | vynásobení délky větví hodnotou x (jedná se o reálné číslo) |
| '(x) | vynásobení délky větví hodnotou x (jedná se o reálné číslo) |
Podobně můžeme měnit tloušťku kreslených větví pomocí příkazů:
| Symbol | Význam symbolu |
|---|---|
| ? | zvýšení faktoru tloušťky větví o koeficient 1,4 (vynásobení délky touto hodnotou) |
| ! | snížení faktoru tloušťky větví o koeficient 0,7 (vynásobení délky touto hodnotou) |
| ?(x) | vynásobení tloušťky větví hodnotou x (jedná se o reálné číslo) |
| !(x) | vynásobení tloušťky větví hodnotou x (jedná se o reálné číslo) |
2. Praktické příklady změny tloušťky a délky větví
Některé příkazy uvedené v předchozí kapitole si můžeme vyzkoušet na praktických příkladech. Nejprve si ukážeme velmi jednoduchý L-systém, který vykreslí takzvaný binární strom (souvislost s odpovídající grafovou a současně i datovou strukturou je z jeho tvaru zřejmá). Binární strom je v našem případě vykreslen v ploše x-y a jeho větvení je zajištěno pomocí želvích příkazů [ a ], které zajistí uložení popř. vyjmutí stavu želvy na interní zásobník stavů (stavových vektorů). První návrh L-systému pro binární strom může vypadat následovně:
# Demonstracni L-system cislo 2.1
# vykresleni binarniho stromu
8 # hloubka rekurze
30 # implicitni uhel natoceni zelvy
30 # tloustka vetvi
&(90)+(90)X # axiom (natoceni zelvy do roviny x-y)
X=F[+X][-X] # prepisovaci pravidlo - vytvoreni kmenu a dvou vetvi
@ # konec specifikace objektu Obrázek 1: Tvar demonstračního L-systému 2.1
Z prvního obrázku vidíme, že výsledný model zdaleka není dokonalý. Můžeme například chtít, aby se u každého větvení zmenšila délka větví na 90% původní velikosti, tj. vynásobila se hodnotou 0,9. Z tabulky uvedené v první kapitole víme, že tuto funkcionalitu zajistí příkaz ', a jelikož je každé větvení zapsáno v samostatných „zásobníkových“ závorkách (pravá hranatá závorka obnoví stav želvy a tím i nastavenou délku větví), můžeme náš L-systém upravit do následující podoby:
# Demonstracni L-system cislo 2.2
# Vykresleni binarniho stromu s ruznymi delkami vetvi
8 # hloubka rekurze
30 # implicitni uhel natoceni zelvy
30 # tloustka vetvi
&(90)+(90)X # axiom (natoceni zelvy do roviny x-y)
X=F['+X]['-X] # prepisovaci pravidlo - vytvoreni kmenu a dvou kratsich vetvi
@ # konec specifikace objektu Obrázek 2: Tvar demonstračního L-systému 2.2
Pokud se nad problémem vytváření binárního stromu zamyslíme, zjistíme, že původní délku větví už v dalších iteracích nebudeme potřebovat. Proto je možné provést malou optimalizaci, kdy se příkaz ' vloží již před „zásobníkové“ závorky, ve kterých se tvoří rozvětvení. Tato optimalizace možná na první pohled může vypadat jako nadbytečná, ovšem u L-systémů, ve kterých se provádí mnoho přepisů a používají se složitá přepisovací pravidla, se může na výsledném řetězci ušetřit i několik stovek kilobytů dat. V našem případě se jedná o hodnoty 2561 a 2306 znaků uložených ve výsledném řetězci (pro hloubku rekurze nastavenou na 8). Optimalizovaná verze L-systému vypadá následovně:
# Demonstracni L-system cislo 2.3
# Vykresleni binarniho stromu s ruznymi delkami vetvi
8 # hloubka rekurze
30 # implicitni uhel natoceni zelvy
30 # tloustka vetvi
&(90)+(90)X # axiom (natoceni zelvy do roviny x-y)
X=F'[+X][-X] # prepisovaci pravidlo - vytvoreni kmenu a dvou kratsich vetvi
@ # konec specifikace objektu Obrázek 3: Tvar demonstračního L-systému 2.3
Spolu s délkou větví se proporcionálně zmenšuje i jejich tloušťka. Na dalším příkladu je ukázáno, jakým způsobem je možné zkombinovat příkazy pro zmenšení délky větví i zúžení jejich šířky. Všimněte si, že místo implicitních hodnot (0,9 resp. 0,7) bylo provedeno dosazení hodnot vlastních. Ty jsou umístěny v závorkách těsně za příkazem ' a !:
# Demonstracni L-system cislo 2.4
# Vykresleni binarniho stromu s ruznymi delkami a tloustkami vetvi
8 # hloubka rekurze
30 # implicitni uhel natoceni zelvy
30 # tloustka vetvi
&(90)+(90)X # axiom (natoceni zelvy do roviny x-y)
X=F'(0.7)!(0.9)[+X][-X] # prepisovaci pravidlo - vytvoreni kmenu, zmena delky a tlousky vetvi, provedeni vetveni
@ # konec specifikace objektu Obrázek 4: Tvar demonstračního L-systému 2.4
Co když nám však nevyhovuje, aby se spolu se zkrácením větví měnila i jejich tloušťka? Není nic jednoduššího, než provést kombinaci změny délky větví pomocí příkazu ' a vynásobení tloušťky převrácenou hodnotou koeficientu délky (to se provádí příkazem !). Pokud se například délka větví snížila na 90% (koeficient=0,9), je možné jejich tloušťku vynásobit hodnotou 0,9-1. Na dalším příkladu modifikovaného binárního stromu je tento princip ukázán v praxi. Úhel natočení želvy je pro lepší ilustraci nastaven na 60° a tloušťka větví na 5% jejich délky. Po změně délky větví v přepisovacím řetězci na polovinu je jejich tloušťka vynásobena hodnotou 2, tj. ve skutečnosti nedojde ani k jejímu zvětšení ani zmenšení:
# Demonstracni L-system cislo 2.5
# Vykresleni binarniho stromu
6 # hloubka rekurze
60 # implicitni uhel natoceni zelvy
5 # tloustka vetvi
&(90)+(90)X # axiom (natoceni zelvy do roviny x-y)
X=F'(0.5)!(2.0)[+X][-X] # prepisovaci pravidlo - vytvoreni kmenu, zmena delky, vetveni
@ # konec specifikace objektu Obrázek 5: Tvar demonstračního L-systému 2.5
3. Příkazy určené pro změnu barvy, kterou želva kreslí
V přepisovacím řetězci je možné použít i dvě formy příkazů, pomocí nichž se mění barva vytvářených větví a listů. Jedná se o příkazy:
| Symbol | Význam symbolu |
|---|---|
| c | zvýšení indexu barvy o jedničku |
| c(x) | změna indexu barvy na nastavenou hodnotu 0–15 |
V současnosti Lparser pracuje se šestnácti barvami, které jsou pro některé formy výstupních souborů pevně zadané, v dalších případech však jednoduše měnitelné. To je i případ exportu do programu POV-Ray, při němž je možné v bázových souborech setup1.pov a setup3.pov změnit následující řádky tak, aby výsledná barva odpovídala našim představám (když už jsme u těch změn, je vhodné na konce řádků přidávat znak středníku, protože syntaxe POV-Raye se od vydání DOSové verze Lparseru upravila):
#declare col_0 = colour red 0.8 green 0.498039 blue 0.196078;
#declare col_1 = colour red 0.5 green 0.5 blue 0.5;
#declare col_2 = colour red 1.0;
#declare col_3 = colour red 1.0 green 1.0;
#declare col_4 = colour red 0.2 green 0.7 blue 0.1;
#declare col_5 = colour blue 1.0 green 1.0;
#declare col_6 = colour blue 1.0;
#declare col_7 = colour red 1.0 blue 1.0;
#declare col_8 = colour red 0.439216 green 0.858824 blue 0.576471;
#declare col_9 = colour red 1.0 green 0.498039 blue 0.0;
#declare col_10 = colour red 0.258824 green 0.258824 blue 0.435294;
#declare col_11 = colour red 0.6 green 0.196078 blue 0.8;
#declare col_12 = colour red 0.439216 green 0.576471 blue 0.858824;
#declare col_13 = colour red 0.556863 green 0.137255 blue 0.137255;
#declare col_14 = colour red 0.858824 green 0.858824 blue 0.439216;
#declare col_15 = colour red 0.623529 green 0.623529 blue 0.372549;
4. Praktické příklady změny barvy
Opět si ukážeme dva jednoduché příklady, které budou modifikovat L-systém ve tvaru binárního stromu. V prvním příkladu je barva změněna již před provedením větvení. Výsledkem je binární strom obarvený tak, že každá úroveň větví (se stejnou délkou a samozřejmě i tloušťkou) má nastavenou i stejnou barvu:
# Demonstracni L-system cislo 2.6
# Vykresleni obarvenenho binarniho stromu
8 # hloubka rekurze
30 # implicitni uhel natoceni zelvy
30 # tloustka vetvi
&(90)+(90)X # axiom (natoceni zelvy do roviny x-y)
X=F'(0.7)!(0.9)c[+X][-X] # prepisovaci pravidlo - zmena barvy pred vetvenim
@ # konec specifikace objektu Obrázek 6: Tvar demonstračního L-systému 2.6
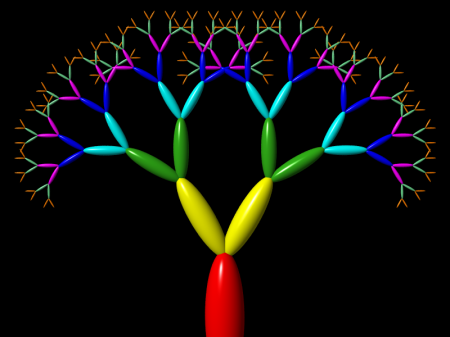
Ve druhém příkladu je barva změněna pouze v jedné větvi, ale vzhledem k prováděné rekurzi se tato změněná barva projeví i na všech následnících. Výsledkem je binární strom obarvený tak, že exisuje jedna „červená cesta“ od kmene až k listům, ze které vyrůstají větve s postupně měněnou barvou (žlutou, zelenou atd.):
# Demonstracni L-system cislo 2.7
# Vykresleni binarniho stromu
8 # hloubka rekurze
30 # implicitni uhel natoceni zelvy
30 # tloustka vetvi
&(90)+(90)X # axiom (natoceni zelvy do roviny x-y)
X=F'(0.7)!(0.9)[c+X][-X] # prepisovaci pravidlo - zmena barvy uvnitr jednoho vetveni
@ # konec specifikace objektu Obrázek 7: Tvar demonstračního L-systému 2.7
Mimochodem: dvojice takto systematicky obarvených binárních stromů je možné použít například při výuce abstraktních datových struktur typu „strom“, zejména při vysvětlování průchodů stromem typu „preorder“, „inorder“ a „postorder“.
5. Orientace v prostoru – nakreslení souřadných os
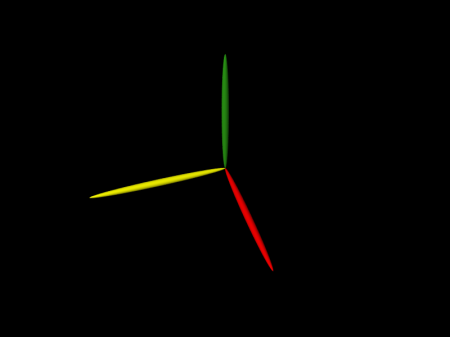
V předchozí části tohoto seriálu jsme si také řekli, jaké příkazy je možné použít pro změnu orientace želvy v prostoru. Tyto příkazy, konkrétně se jedná o + a ^, nyní použijeme pro snad nejjednodušší prostorový objekt, který je možné s pomocí Lparseru vytvořit. Jedná se o souřadné osy vytvořené pomocí trojice větví, které se střetávají v počátku souřadné soustavy. Celý L-systém je možné zapsat následujícím způsobem (všimněte si, že díky použití implicitního úhlu natočení želvy na 90° není nutné tento úhel při natáčení želvy specifikovat):
# Demonstracni L-system cislo 2.8
# Vykresleni souradnych os
2 # hloubka rekurze
90 # implicitni uhel natoceni zelvy
5 # tloustka vetvi
&X # axiom
X=[ABC] # prvni pravidlo - vykresleni vsech tri os
A=[c(2)Z] # prvni osa vykreslena cervenou barvou
B=[c(3)+Z] # druha osa vykreslena zlutou barvou
C=[c(4)^Z] # treti osa vykreslena zelenou barvou
@ # konec specifikace objektu Obrázek 8: Tvar demonstračního L-systému 2.8
Proč si zde uvádíme vykreslení souřadných os, když se jedná o zcela nezajímavý model? V případě, že se při tvorbě složitějšího L-systému „ztratíme“, je vhodné si na určitém místě (třeba i uprostřed jiného přepisovacího pravidla) nechat vykreslit lokální souřadný systém želvy. A právě k tomuto účelu se dále uvedená čtveřice přepisovacích pravidel X, A, B, C hodí. Vzhledem k tomu, že jsou použity „zásobníkové“ závorky, neovlivní vykreslení souřadných os celý L-systém, protože se vše vrátí do původního nastavení. V případě potřeby vykreslení více pozic želvy ve složitém L-systému se mohou jednotlivé souřadné osy odlišit například barvou nebo tloušťkou větví – vše se nastavuje v přepisovacím pravidlu X uvnitř závorek.
6. Vytváření 3D modelů stromů
Spolu s DOSovskou verzí Lparseru je dodáváno několik demonstračních L-systémů, které je možné použít při tvorbě trojrozměrných modelů stromů. Tyto L-systémy jsou uloženy v souborech pojmenovaných „tree00.ls“ až „tree11.ls“. Pro další testování (kterým se budeme zabývat především v následující části tohoto seriálu) se nejvíce hodí L-systém uložený v souboru „tree02.ls“. Následuje výpis tohoto L-systému i s komentáři. Všimněte si zejména použití příkazu „t“, kterým se aplikuje gravitace – bez tohoto příkazu by byly větve nepřirozeně vzpřímené:
# Demonstracni L-system cislo 2.9
# Vykresleni trojrozmerneho modelu stromu
15 # hloubka rekurze (prepisu retezce)
30 # implicitni uhel natoceni zelvy
20 # relativni tloustka vetvi
#
FA # axiom (kmen a vetveni)
#
A=!(.9)t(.4)FB>(94)B>(132)B
B=[&t(.4)F$A]
F='(1.25)F'(.8) # kmen (1.25=1/0.8)
@ # konec specifikace objektu Obrázek 9: Tvar demonstračního L-systému 2.9
7. Demonstrační příklad – interaktivní prohlížení souborů typu RAW
Pro účely snadného zobrazování trojrozměrných modelů vytvářených pomocí programu Lparser je určen dnešní jediný demonstrační příklad. Zobrazení vygenerovaných modelů je tedy možné i bez instalace programu POV-Ray či prohlížečky formátu VRML, se kterými mohou být problémy. Aplikace, která vznikne překladem tohoto demonstračního příkladu, umožňuje načíst model uložený do formátu RAW. To je textový (ASCII) soubor obsahující seznam trojúhelníků, přičemž je možné tento model nasvítit dvěma zdroji světla, provádět interaktivně ovládané rotace modelu na obrazovce a posun modelu směrem od a ke kameře apod.
Při spouštění programu postačí jako jediný parametr zadat jméno souboru ve formátu RAW, tento soubor se v Lparseru vytvoří zadáním modifikátoru -R (R musí být v tomto případě zapsáno velkým písmenem). Ovládání je popsáno v následující tabulce. Zdrojový kód tohoto demonstračního příkladu je dostupný jak ve formě zdrojového textu, tak i jako HTML stránka se zvýrazněnou syntaxí.
| Operace (klávesa) | Význam |
|---|---|
| Esc | ukončení běhu aplikace |
| Q | ukončení běhu aplikace |
| 1 | zobrazení pouze vrcholů trojúhelníků |
| 2 | zobrazení drátového modelu |
| 3 | zobrazení vystínovaného modelu |
| levé tlačítko myši | rotace modelu |
| pravé tlačítko myši | posun modelu |
8. Screenshoty trojrozměrných modelů L-systémů zobrazených v demonstračním příkladu
Na následujících obrázcích jsou uvedeny screenshoty modelů vygenerovaných pomocí L-systémů popsaných v předchozích kapitolách.

Obrázek 10: Screenshot s L-systémem 2.1

Obrázek 11: Screenshot s L-systémem 2.2

Obrázek 12: Screenshot s L-systémem 2.3

Obrázek 13: Screenshot s L-systémem 2.4

Obrázek 14: Screenshot s L-systémem 2.5

Obrázek 15: Screenshot s L-systémem 2.6

Obrázek 16: Screenshot s L-systémem 2.7

Obrázek 17: Screenshot s L-systémem 2.8

Obrázek 18: Screenshot s L-systémem 2.9
9. Obsah dalšího pokračování tohoto seriálu
V následujícím pokračování tohoto seriálu si ukážeme způsoby další modifikace vytvářených objektů. Bude se jednat o aplikaci gravitace, kterou je vhodné aplikovat zejména na modely přírodních struktur, a mutace, které mění zapisovaná pravidla a vnáší tak do L-systémů jistý prvek náhodnosti. Nakonec si ukážeme již minule slibovanou tvorbu animací.