Obsah
1. Procedura qix a průběžná změna jejích parametrů
2. Tvorba trojrozměrné grafiky v Logu
3. Přechod z 2D plochy do 3D prostoru
4. Želva a její orientace v trojrozměrném prostoru
5. Základní postupy použité při tvorbě 3D modelů
6. Demonstrační příklad – jednoduchý drátový model vykreslený s využitím absolutního pozicování
7. Demonstrační příklad – druhá verze tvorby drátového modelu
8. Demonstrační příklad – želví grafika ve 3D
9. Obsah následující části tohoto seriálu
1. Procedura qix a průběžná změna jejích parametrů
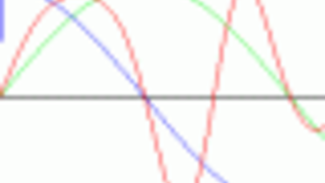
V předchozí části tohoto seriálu jsme si ukázali způsob tvorby animací spolu s jejich ukládáním do souborů typu GIF. Nejedná se sice o ten nejúspornější animační formát, ale prakticky každý uživatel vlastnící webový prohlížeč si může takto vytvořené animace zobrazit na svém počítači. Problematiku animací zakončíme demonstračním příkladem, ve kterém se proceduře qix (tu již známe z předchozích částí tohoto seriálu, její jméno je inspirované prastarou počítačovou hrou) postupně předávají odlišné parametry pro tvorbu obrazce. Výsledné snímky jsou ukládány ve formě animace. V proceduře qix jsou počítány koncové body úseček, jež se pohybují po drahách majících tvar takzvaných Lissajousových obrazců. Této proceduře je nutné předat počet opakování smyčky (tj. kolik úseček se má vytvořit), „amplitudu“ Lissajousových obrazců (maximální vzdálenost vygenerovaných bodů od počátku souřadné soustavy) a nakonec také čtyři reálné hodnoty, které představují násobek základní frekvence a pomocí nichž se určuje vlastní tvar obrazce.
V seznamu testdata jsou uloženy parametry čtyř obrazců (pro každý obrazec se jedná o jeden vektor čtyř reálných hodnot). Pro dosažení plynulé animace je nutné, aby se mezi těmito parametry prováděla lineární interpolace a výsledný vektor byl použit pro výpočet a následné vykreslení obrazce. To je zařízeno v proceduře nazvané calc_params, která na základě hodnoty cnt provede lineární interpolaci mezi vektory params1 a params2. Maximální hodnota cnt je v našem případě 40, což také odpovídá počtu snímků vykreslených mezi dvěma krajními obrazci.

Následuje výpis zdrojového kódu dnešního prvního demonstračního příkladu:
; Složitější animace využívající efektu "qix"
; Tento demonstrační příklad byl upraven
; pro MSW Logo s nastavenou aktivní plochou
; o rozměrech [-100, -100] - [100, 100] kroků želvy
; Vytvoření obrazce složeného z úseček
; význam jednotlivých parametrů:
; opak - počet opakování
; amp - "amplituda", maximální vzdálenost od počátku
; freq - seznam se čtyřmi reálnými hodnotami (násobky frekvence)
to qix :opak :amp :freq
repeat :opak [
; výpočet souřadnic prvního vrcholu úsečky
make "x1 :amp*cos 2*repcount* item 1 :freq
make "y1 :amp*sin 2*repcount* item 2 :freq
; výpočet souřadnic druhého vrcholu úsečky
make "x2 :amp*sin 2*repcount* item 3 :freq
make "y2 :amp*cos 2*repcount* item 4 :freq
; přesun na počáteční pozici (bez kreslení)
penup
setpos list :x1 :y1
; vykreslení úsečky z počáteční do koncové pozice
pendown
setpos list :x2 :y2
]
end
; Výpočet frekvencí pro zadaný snímek animace
; význam jednotlivých parametrů:
; cnt - hodnota v rozsahu 1..40
; params1 - čtveřice první sady frekvencí
; params2 - čtveřice druhé sady frekvencí
to calc_params :cnt :params1 :params2
; pomocné proměnné pro výpočet lineární kombinace
make "p1 (40-repcount)/40
make "p2 1.0-:p1
; výsledný seznam
make "params []
repeat 4 [
make "params lput (item repcount :params1)*:p1+(item repcount :params2)*:p2 :params
]
; vypočtené parametry vytiskneme
show :params
output :params
end
; vlastní vytvoření animace
to test_qix
make "testdata [
[2.0 1.5 1.0 3.5]
[3.0 3.0 2.0 2.0]
[1.0 0.5 0.5 2.0]
[4.0 3.0 2.0 2.0]
]
window
hideturtle
clearscreen
; počáteční snímek
(gifsave "animace_6.gif 15 "False 0 4)
; projdeme celý seznam a pro každou sousední dvojici
; vykreslíme obrazec
repeat 3 [
; dvojice vektorů - počáteční a koncové frekvence
make "params1 item repcount :testdata
make "params2 item repcount+1 :testdata
repeat 40 [
; výpočet lineární kombinace vektorů
make "params calc_params repcount :params1 :params2
clearscreen
qix 200 100 :params
; uložení snímku animace
(gifsave "animace_6.gif 15 "True 0 4)
]
]
end
; spuštění příkladu a vytvoření animace
test_qix Po úpravě seznamu testdata tak, aby obsahoval s parametry:
[3.0 3.0 2.0 2.0]
[2.0 1.5 1.0 3.5]
[4.0 3.0 2.0 2.0]
[1.0 0.5 0.5 2.0]
[2.0 3.5 1.5 2.0] a změně hlavní programové smyčky ze tří na čtyři opakování získáme následující animaci:

2. Tvorba trojrozměrné grafiky v Logu
Ve všech předchozích částech tohoto seriálu, ve kterých jsme se zabývali želví grafikou, byly popisovány procedury určené pro vykreslování obrázků v dvourozměrné grafické ploše (takzvaná 2D grafika). V mnoha implementacích tohoto programovacího jazyka se opravdu setkáme „pouze“ s tradiční dvourozměrnou grafikou, která je na ovládání i pochopení snazší, nehledě na nižší systémové nároky 2D grafiky. Mnoho implementací Loga bylo určeno pro osmibitové počítače řady Atari, Apple II, Commodore či ZX-Spectrum, na kterých je 3D grafika sice použitelná (hry typu Elite, Mercenary, Rescue on Fractalus apod.), ale s různými omezeními danými jak rychlostí procesoru a kapacit použitých pamětí, tak i grafickým režimem.
S rostoucí výkonností mikroprocesorů i grafických čipů však v minulém desetiletí došlo k velkému nárůstu aplikací pracujících s trojdimenzionální (3D) grafikou i na běžných osobních počítačích. I z tohoto důvodu některé moderní implementace Loga do repertoáru svých procedur zahrnují příkazy pro práci s prostorovými modely. Zatímco v 2D grafice byla základním stavebním prvkem vytvářených obrázků úsečka vytvářená při pohybu želvy, v případě 3D grafiky se pro tvorbu drátových modelů používají prostorové úsečky a pro tvorbu stínovaných modelů vyplněné plošné polygony (mnohoúhelníky). V dalších kapitolách budou popsány postupy a procedury platné pro MSW Logo a částečně také pro aUCB Logo. Mezi další implementace Loga, které práci v prostoru podporují, patří například Elica.
Obrázek 3: Trojrozměrný model vytvořený v aUCB Logu
3. Přechod z 2D plochy do 3D prostoru
Při práci s dvourozměrnou grafickou plochou Loga se želva po této ploše pohybuje (přesněji řečeno, je ovládána) pomocí dvou množin příkazů. V první množině se nachází příkazy, které slouží k takzvanému relativnímu pohybu želvy. Mezi tyto příkazy patří známé procedury forward (pohyb želvy ve směru její orientace o zadaný počet kroků), back (pohyb želvy zpět, tj. proti směru její orientace, o zadaný počet kroků), left (natočení želvy doleva o zadaný počet stupňů) a right (natočení želvy doprava o zadaný počet stupňů), ke kterým se přidává procedura home, jež želvu vrátí zpět na počátek souřadného systému dvourozměrné plochy, tj. na souřadnice [0, 0]. Podobný účinek má i procedura clearscreen, která navíc ještě vymaže celou viditelnou část grafické plochy.
Obrázek 4: Fraktálový strom vytvořený v aUCB LoguDruhá množina příkazů, kterou již někteří autoři-puristé ani nezapočítávají do želví grafiky, nastavuje želvu na zadané absolutní souřadnice nebo ji natočí do určitého směru, nezávisle na její aktuální poloze či orientaci. Mezi tyto příkazy se řadí procedury typu setpos (nastavení obou souřadnic želvy na předávanou hodnotu), setx (nastavení pouze x-ové souřadnice, druhá souřadnice zůstane nezměněna), sety (nastavení pouze y-ové souřadnice, první souřadnice zůstane nezměněna), setxy (jiná podoba procedury setpos, při jejímž volání se místo jednoho seznamu souřadnic použije dvojice hodnot) a setheading (nastavení orientace želvy na zadaný úhel). Procedura home vlastně svým účinkem spadá do obou kategorií, tj. jak mezi procedury určené pro relativní pohyb želvy, tak i mezi procedury určené pro nastavení souřadnic na absolutní hodnotu.
Obrázek 5: Drátový model (wireframe) vykreslovaný v MSW LoguV dvourozměrné ploše je stav želvy popsán dvojicí souřadnic [x, y] (lze je přečíst například funkcí pos) a orientací zapsanou ve stupních (tu lze zjistit, tj. přečíst funkcí heading). Při přechodu z dvourozměrné grafické plochy do trojrozměrného prostoru musí být stav želvy popsán větším množstvím údajů. Samozřejmě se zvětší počet souřadnic, které popisují polohu želvy v prostoru. Místo dvojice souřadnic je použita trojice souřadnic [x, y, z]. Pro nastavení želvy na absolutní trojrozměrné souřadnice slouží procedury vypsané v následující tabulce:
| Procedura | Význam |
|---|---|
| setxyz | nastavení želvy na souřadnice určené trojicí parametrů |
| setz | nastavení třetí, tj. z-ové souřadnice želvy |
| setposxyz | podobné první proceduře, ale předává se seznam tří hodnot |
| home | je možné využít i v 3D prostoru |
4. Želva a její orientace v trojrozměrném prostoru
Složitější je však situace s orientací želvy v prostoru. Zatímco v ploše jsme si vystačili s jediným údajem (natočením želvy, heading) a trojicí procedur left, right a setheading, v trojrozměrném prostoru se želva může natáčet okolo svých tří lokálních souřadných os (vektorů). Pro lepší přiblížení si můžeme místo želvy představit letadlo, které může zatáčet doprava a doleva (beze změny výšky), nahoru a dolů (beze změny kurzu) a také se může natáčet ve směru osy svého letu. Tyto směry, resp. jejich změny se v angličtině nazývají roll, pitch a heading.
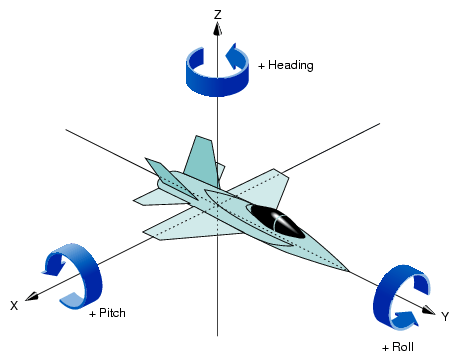
Pro (absolutní či relativní) změnu natočení želvy/letadla v některém z těchto směrů se používají následující procedury:
| Procedura | Význam |
|---|---|
| left | relativní změna směru heading |
| right | relativní změna směru heading |
| setheading | nastavení směru heading na předanou hodnotu |
| leftroll | relativní změna směru roll |
| rightroll | relativní změna směru roll |
| setroll | nastavení směru roll na předanou hodnotu |
| uppitch | relativní změna směru pitch |
| downpitch | relativní změna směru pitch |
| setpitch | nastavení směru pitch na předanou hodnotu |
| setorientation | nastavení všech tří směrů podle seznamu [roll pitch heading] |
Při tvorbě takzvaných drátových modelů (wireframe) vystačíme s procedurami vypsanými v předchozích dvou tabulkách. K těmto procedurám je nutné připočíst dvojici nám již známých příkazů forward a back, které želvou posunují v 3D prostoru ve směru jejího natočení (v úvahu se berou všechny tři údaje roll, pitch i heading).
Obrázek 7: Želva po ukončení kreslení v MSW Logu
5. Základní postupy použité při tvorbě 3D modelů
Před jakoukoli prací s 3D modely je nutné provést přepnutí zobrazení z grafické 2D plochy do 3D prostoru. To se v MSW Logu i dalších implementacích tohoto programovacího jazyka provádí příkazem perspective. Následně je vhodné nastavit pozici pozorovatele (kamery) na nějaké souřadnice. Implicitně se předpokládá, že se kamera „dívá“ na počátek souřadného systému. Pozice kamery je pro jednoduchost reprezentována speciální želvou s číslem –1, pozice bodu, na který se kamera dívá, pak želvou s číslem –2. Celý postup nastavení 3D zobrazení je vhodné uzavřít do pojmenované procedury tak, jak je ukázáno na následujícím výpisu (pozice bodu, na který se kamera dívá, není změněna):
to turnon3d
; přepnutí do perspektivního režimu
perspective
; speciální číslo želvy reprezentující kameru
setturtle -1
; přesun želvy (kamery) na zadané absolutní souřadnice
setxyz 500 500 500
; nastavení původní (defaultní) želvy
setturtle 0
end
6. Demonstrační příklad – jednoduchý drátový model vykreslený s využitím absolutního pozicování
Pravděpodobně nejjednodušší formou tvorby trojrozměrných modelů je použití absolutního pozicování želvy na stanovené trojrozměrné souřadnice pomocí procedury setxyz. Želva při svém přesunu na nové souřadnice vykreslí (samozřejmě, pokud je kreslicí pero spuštěno) úsečku. Vhodným zvedáním a spouštěním kreslicího pera s přesunem želvy je možné vytvářet prakticky libovolné trojrozměrné tvary složené pouze z hran – to je základ drátových modelů (wireframe). Tento postup je ukázán i na dalším demonstračním příkladu, ve kterém je vykreslena krychle reprezentovaná dvanácti hranami. Všimněte si nutnosti vypínat vykreslování (zvednout kreslicí pero) v případě, že se želva nepřesouvá po hranách, ale po úhlopříčkách:
; První verze příkladu na vykreslení drátové krychle
; pomocí absolutního pozicování želvy
; Tento demonstrační příklad byl upraven
; pro MSW Logo běžící na systémech
; s minimálně 256 barvami
to abs_cube
perspective
clearscreen
setpencolor 1
setxyz 0 0 0
setxyz 100 0 0
setxyz 100 100 0
setxyz 0 100 0
setxyz 0 0 0
penup
setpencolor 2
setxyz 0 0 100
pendown
setxyz 100 0 100
setxyz 100 100 100
setxyz 0 100 100
setxyz 0 0 100
setpencolor 4
penup
setxyz 100 0 0
pendown
setxyz 100 0 100
penup
setxyz 100 100 0
pendown
setxyz 100 100 100
penup
setxyz 0 100 0
pendown
setxyz 0 100 100
penup
setxyz 0 0 0
pendown
setxyz 0 0 100
end 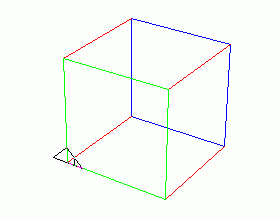
7. Demonstrační příklad – druhá verze tvorby drátového modelu
Předchozí příklad je možné zjednodušit tak, že si vytvoříme pomocnou proceduru pro vykreslení úsečky v trojrozměrném prostoru. Tato procedura je vlastně velmi jednoduchá: nejdříve se zvedne kreslicí pero a želva se přesune do prvního vrcholu úsečky. Posléze je kreslicí pero spuštěno a želva se přesune do druhého vrcholu, přičemž vykreslí požadovanou úsečku. Při použití této procedury je nutné mít na mysli, že dojde k narušení původní pozice želvy a také barvy i stavu kreslicího pera. V případě nutnosti je možné stav želvy uložit do lokálních proměnných a po provedení vykreslení 3D úsečky opět stav želvy plně obnovit:
; Druhá verze příkladu na vykreslení drátové krychle
; pomocí absolutního pozicování želvy
; Tento demonstrační příklad byl upraven
; pro MSW Logo s běžící na systémech
; s minimálně 256 barvami
; Pomocná procedura pro vykreslení
; obarvené úsečky v 3D prostoru
to line3d :bod1 :bod2 :barva
; nastavení barvy vykreslování
setpencolor :barva
; přesun do prvního bodu (bez kreslení)
penup
setposxyz :bod1
; přesun do druhého bodu (s kreslením)
pendown
setposxyz :bod2
end
to abs_cube2
perspective
clearscreen
line3d [ 0 0 0] [ 0 0 100] 1
line3d [100 0 0] [100 0 100] 1
line3d [ 0 100 0] [ 0 100 100] 1
line3d [100 100 0] [100 100 100] 1
line3d [0 0 0] [100 0 0] 2
line3d [0 0 100] [100 0 100] 2
line3d [0 100 0] [100 100 0] 2
line3d [0 100 100] [100 100 100] 2
line3d [ 0 0 0] [ 0 100 0] 4
line3d [ 0 0 100] [ 0 100 100] 4
line3d [100 0 0] [100 100 0] 4
line3d [100 0 100] [100 100 100] 4
end 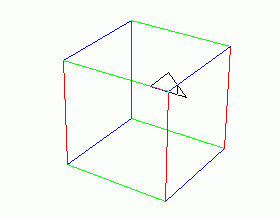
8. Demonstrační příklad – želví grafika ve 3D
V předchozích dvou příkladech bylo použito absolutní pozicování želvy. To je sice jednodušší na pochopení, ale mnoho zajímavých modelů je možné programově využít s relativním pozicováním, tj. se „skutečnou“ želví grafikou. V dalším příkladu je vytvořen trojrozměrný květ pomocí deseti krychlí, z nichž každá je natočena o 36° Všimněte si zejména způsobu použití procedur right, downpitch a leftroll:
to cube
repeat 4 [
repeat 4 [
forward 100
right 90
]
forward 100
downpitch 90
]
to cubes
repeat 10 [
cube
leftroll 36
]
end 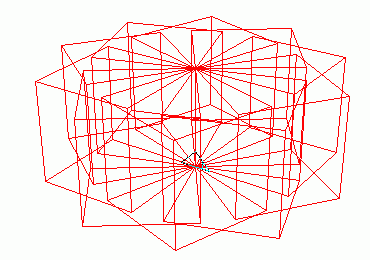
9. Obsah následující části tohoto seriálu
V poslední části seriálu o programovacím jazyce Logo dokončíme téma trojrozměrné grafiky popisem použití vyplněných polygonů a jednoduchého osvětlovacího modelu. Také bude uveden soupis literatury a většiny příkazů, se kterými jsme se v tomto seriálu seznámili.