Obsah
1. Tvorba grafů a diagramů s využitím doménově specifického jazyka nástroje Graphviz
2. Vztah nástroje Graphviz a již popsaných nástrojů určených pro tvorbu diagramů a grafů
5. Graf s větším množstvím uzlům a neorientovanými hranami
7. Grafy s orientovanými hranami
8. Nepatrně složitější grafy s orientovanými hranami
10. Další modifikace způsobu vykreslení grafu: uspořádání uzlů zleva doprava
13. HTML entity v popiskách hran i uzlů
14. Graf se šesticí uzlů vykreslený nástrojem dot
15. Různé algoritmy pro rozmístění uzlů aneb praktická ukázka filozofie „rozděl a panuj“
16. Graf se šesticí uzlů vykreslený nástrojem circo
17. Další grafy vykreslené nástrojem circo
18. Repositář s demonstračními příklady
19. Odkazy na články s tématem programové tvorby grafů a diagramů
1. Tvorba grafů a diagramů s využitím doménově specifického jazyka nástroje Graphviz
V mnoha dokumentech, popř. v různých reportech (někdy i automaticky generovaných) je nutné vytvářet diagramy s uzly propojenými neorientovanými či orientovanými hranami. Pro tento účel je vhodné ve většině případů použít balíček nástrojů nazvaný Graphviz. V tomto balíčku nalezneme především utilitu nazvanou dot, která na základě textové definice orientovaného či neorientovaného grafu vytvoří rastrový či vektorový obrázek s grafem, přičemž je možné zvolit, jaký algoritmus bude použit pro rozmístění uzlů a hran na vytvořeném obrázku. Modifikovat lze i další vlastnosti grafu, především styl vykreslení hran, rozmístění uzlů grafu apod. Textová definice grafu používá jednoduchý popisný jazyk (samozřejmě doménově specifický), který je v současnosti podporován i několika dalšími nástroji a stává se tak nepsaným standardem pro mnoho aplikací pracujících s grafovými strukturami.
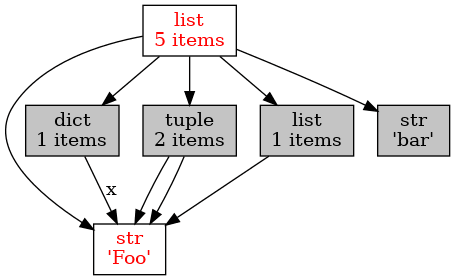
Obrázek 1: Nástroj Graphviz lze použít i pro vizualizaci objektů uložených v operační paměti (Python).
2. Vztah nástroje Graphviz a již popsaných nástrojů určených pro tvorbu diagramů a grafů
Nástroj Graphviz se velmi často používá ve funkci backendu využívaného dalšími front-endovými nástroji a knihovnami. Tyto nástroje/knihovny, ať již se ovládají programově nebo interaktivně, vytváří definice grafů kompatibilních s Graphviz a následně je Graphviz zavolán pro vizualizaci těchto grafů. Tímto způsobem pracuje například knihovna Rhizome, se kterou jsme se seznámili v tomto článku.
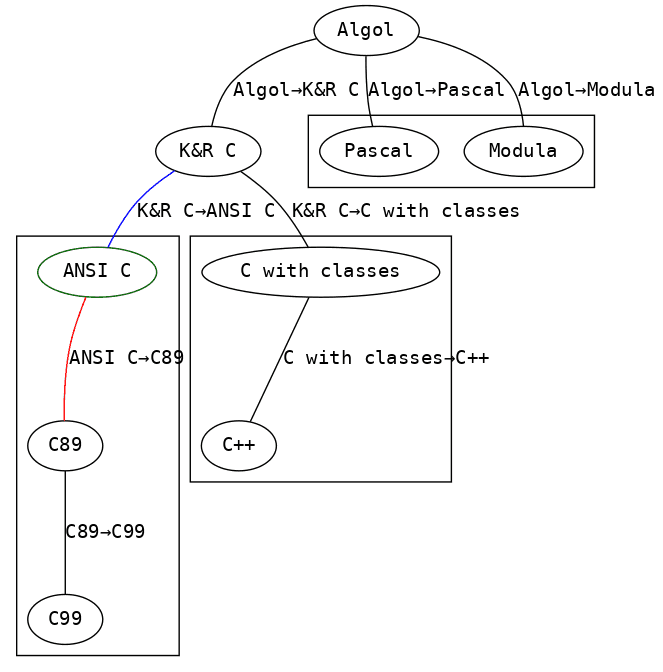
Obrázek 2: Graf vykreslený knihovnou Rhizome určenou pro Clojure.
Nad nástrojem Graphviz je postavena i knihovna Diagrams (pro Python) a go-diagrams (pro Go). S oběma těmito knihovnami jsme se seznámili v článcích Tvorba diagramů s architekturou systémů s využitím knihovny Diagrams a Knihovny Diagrams a go-diagrams určené pro tvorbu diagramů s architekturou systémů .
Obrázek 3: Architektura nakreslená knihovnou Diagrams určenou pro Python.
3. Graf s jediným uzlem
Ukažme si nyní ten nejjednodušší graf, který je možné s využitím nástroje Graphviz vykreslit. Tento graf bude obsahovat jediný uzel a žádnou hranu. Definice takového graf může vypadat následovně:
graph {
a;
}
V případě, že je definice tohoto grafu uložena do souboru nazvaného graph01.dot, lze vykreslení grafu do rastrového obrázku zajistit tímto příkazem:
$ dot -Tpng graph01.dot > graph01.png
Obrázek 4: Graf s jediným uzlem bez hran vykreslený předchozím příkazem.
4. Volba výstupního formátu
Nástroj dot a současně i další nástroje z balíčku Graphviz, podporují několik výstupních formátů, které se volí přepínačem -T:
| # | Přepínač | Výstupní formát | Poznámka |
|---|---|---|---|
| 1 | -Tps | PostScript | metaformát |
| 2 | -Tsvg | Scalable Vector Graphics | vektorový formát |
| 3 | -Tsvgz | Gzipped Scalable Vector Graphics | vektorový formát |
| 4 | -Tfig | XFIG graphics | vektorový formát |
| 5 | -Tpng | Formát PNG | rastrový formát |
| 6 | -Tgif | Formát GIF | rastrový formát |
| 7 | -Tjpg | Formát JPEG | rastrový formát |
| 8 | -Timap | server-side imagemap | metaformát |
| 9 | -Tcmapx | client-side imagemap | metaformát |
0 0 1 beginpage gsave 36 36 62 44 boxprim clip newpath 1 1 set_scale 0 rotate 40 40 translate % a gsave 1 setlinewidth 0 0 0 nodecolor 27 18 27 18 ellipse_path stroke 0 0 0 nodecolor 14 /Times-Roman set_font 23.5 14.3 moveto 7 (a) alignedtext grestore endpage showpage
Ještě si pro úplnost ukažme způsob exportu do formátu SVG neboli Scalable Vector Graphics:
<?xml version="1.0" encoding="UTF-8" standalone="no"?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd"> <!-- Generated by graphviz version 2.36.0 (20140111.2315) --> <!-- Title: %3 Pages: 1 --> <svg width="62pt" height="44pt" viewBox="0.00 0.00 62.00 44.00" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink"> <g id="graph0" class="graph" transform="scale(1 1) rotate(0) translate(4 40)"> <title>%3</title> <polygon fill="white" stroke="none" points="-4,4 -4,-40 58,-40 58,4 -4,4"/> <!-- a --> <g id="node1" class="node"><title>a</title> <ellipse fill="none" stroke="black" cx="27" cy="-18" rx="27" ry="18"/> <text text-anchor="middle" x="27" y="-14.3" font-family="Times,serif" font-size="14.00">a</text> </g> </g> </svg>
Po naformátování příkazem:
$ xmllint --format graph1.svg > graph1B.svg
Získáme relativně snadno čitelný soubor s tímto obsahem:
<?xml version="1.0" encoding="UTF-8" standalone="no"?>
<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">
<!-- Generated by graphviz version 2.36.0 (20140111.2315)
-->
<!-- Title: %3 Pages: 1 -->
<svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" width="62pt" height="44pt" viewBox="0.00 0.00 62.00 44.00">
<g id="graph0" class="graph" transform="scale(1 1) rotate(0) translate(4 40)">
<title>%3</title>
<polygon fill="white" stroke="none" points="-4,4 -4,-40 58,-40 58,4 -4,4"/>
<!-- a -->
<g id="node1" class="node">
<title>a</title>
<ellipse fill="none" stroke="black" cx="27" cy="-18" rx="27" ry="18"/>
<text text-anchor="middle" x="27" y="-14.3" font-family="Times,serif" font-size="14.00">a</text>
</g>
</g>
</svg>
5. Graf s větším množstvím uzlům a neorientovanými hranami
Pochopitelně nám nic nebrání ve vytvoření grafu s větším počtem uzlů, které jsou propojeny neorientovanými hranami. Příkladem může být graf s dvojicí uzlů propojených jedinou hranou, která není orientována (tedy nejedná se o šipku, ale o pouhou spojnici):
graph {
a -- b;
}
Tento graf se vykreslí následujícím způsobem:
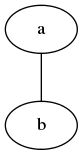
Obrázek 5: Graf s dvojicí uzlů propojených neorientovanou hranou.
Ve skutečnosti je možné vytvořit i hrany, které začínají i končí ve stejném uzlu, což se poměrně často používá například u konečných automatů atd. Podívejme se tedy na další demonstrační příklad:
graph {
a -- b;
a -- a;
b -- b;
}
V tomto grafu se nakreslí ještě dvojice přidaných hran, první z uzlu A do uzlu A a druhá z uzlu B do uzlu B:
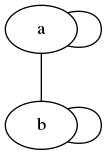
Obrázek 6: Graf s dvojicí uzlů a několika hranami.
Pracovat lze i s grafy, v nichž jsou uzly propojeny větším množstvím hran:
graph {
a -- b;
a -- a;
b -- b;
a -- b;
}
S následujícím výsledkem:
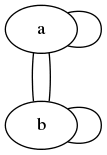
Obrázek 7: Graf s dvojicí uzlů a několika hranami.
6. Popisky hran v grafu
V případě potřeby je možné hrany grafu pojmenovat, což se provede následujícím způsobem:
graph {
a -- b[label="a - b"];
a -- a[label="a - a"];
b -- b[label="b - b"];
a -- b[label="b - a"];
}
Výsledek, tedy vykreslený graf, bude v tomto případě vypadat takto:
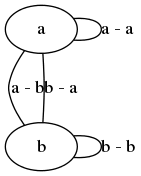
Obrázek 8: Graf s dvojicí uzlů a několika hranami, u kterých jsou specifikovány popisky.
7. Grafy s orientovanými hranami
Dostáváme se ke grafům s orientovanými hranami, tj. hranami vykreslenými formou šipky. V nástroji Graphviz (a nejenom zde) jsou tyto grafy pojmenovány digraph. U těchto grafů záleží na tom, v jakém pořadí zadáváme uzly, mezi nimiž se má vytvořit hrana:
digraph {
a -> b;
}
S tímto výsledkem:
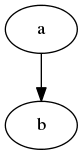
Obrázek 9: Graf s orientovanou hranou.
Pozor na rozdíl oproti grafu, v němž jsou uzly prohozeny:
digraph {
b -> a;
}
S tímto výsledkem:
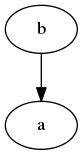
Obrázek 10: Graf s orientovanou hranou, ovšem s opačnou šipkou v porovnání s obrázkem číslo 7.
8. Nepatrně složitější grafy s orientovanými hranami
Další příklad poněkud složitějšího grafu s orientovanými hranami bude vypadat takto:
digraph {
a -> b;
b -> c;
c -> d;
d -> a;
}
S následujícím výsledkem:
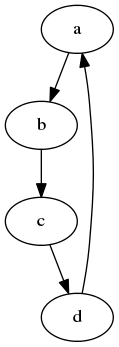
Obrázek 11: Graf se čtveřicí uzlů a orientovanými hranami.
Graf s hranami, které se vrací do původního uzlu:
digraph {
a -> b;
b -> c;
c -> d;
d -> a;
a -> a;
b -> b;
c -> c;
d -> d;
}
V tomto případě získáme tento výsledek:
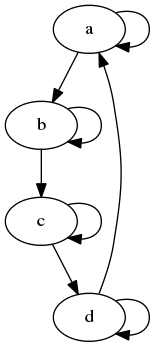
Obrázek 12: Graf s hranami, které se vrací do původního uzlu.
9. Zvýraznění hran v grafu
V grafech je možné některé hrany nebo uzly zvýraznit a zobrazit tak například nalezenou cestu:
graph {
a -- b[label="a - b", color="red", penwidth="2.0"];
a -- a[label="a - a", color="blue", penwidth="2.0"];
b -- b[label="b - b"];
a -- b[label="b - a"];
}
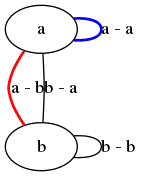
Obrázek 13: Neorientovaný graf se zvýrazněnými hranami.
Tutéž operaci ovšem můžeme provést i pro orientované grafy:
digraph {
a -> b[label="a - b", color="red", penwidth="2.0"];
b -> c[label="b - c", color="red", penwidth="2.0"];
c -> d;
d -> a;
a -> a;
b -> b;
c -> c[label="c - c", color="red", penwidth="2.0"];
d -> d;
}
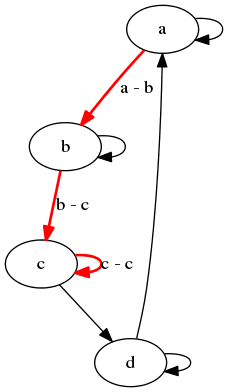
Obrázek 14: Orientovaný graf se zvýrazněnými hranami.
10. Další modifikace způsobu vykreslení grafu: uspořádání uzlů zleva doprava
Podívejme se nyní na vybrané způsoby různých modifikací vykreslení grafu. V některých případech je vhodné změnit uspořádání uzlů v grafu. Při výchozím nastavení jsou uzly (většinou) uspořádány shora dolů, ovšem mnohdy je žádoucí změnit toto uspořádání na zleva doprava. K tomuto účelu slouží přepínač rankdir, který je nutné nastavit na hodnotu LR:
digraph {
rankdir=LR
a -> b[label="a - b", color="red", penwidth="2.0"];
b -> c[label="b - c", color="red", penwidth="2.0"];
c -> d;
d -> a;
a -> a;
b -> b;
c -> c[label="c - c", color="red", penwidth="2.0"];
d -> d;
}
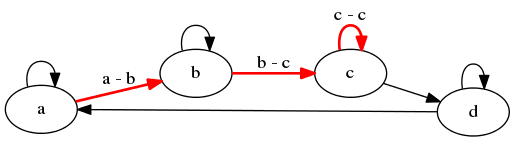
Obrázek 15: Orientovaný graf se zvýrazněnými hranami a s uzly uspořádanými zleva doprava.
11. Přepínač splines
Přepínačem splines nastaveným na hodnotu „line“ je možné vynutit, aby se hrany spojující různé uzly vykreslily formou úsečky a nikoli jako spline křivky. Tato volba ovšem neovlivní hrany začínající a končící ve stejném uzlu (ty jsou stále reprezentovány obloukem). Podívejme se nyní na rozdíl mezi tímto grafem:
digraph {
a -> b;
b -> c;
c -> d;
d -> a;
a -> a;
b -> b;
c -> c;
d -> d;
}
A tímto grafem, v němž je specifikováno, že se namísto spline křivek mají použít úsečky (tedy přesněji řečeno tam, kde je to možné):
digraph {
splines="line"
a -> b;
b -> c;
c -> d;
d -> a;
a -> a;
b -> b;
c -> c;
d -> d;
}
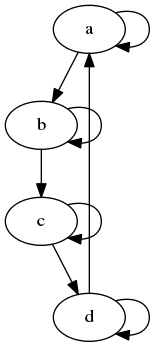
Obrázek 16: Graf s hranami vykreslenými formou úsečky, popř. oblouku.
12. Modifikace uzlů v grafu
Již v předchozích kapitolách jsme si popsali způsob změny grafických (resp. přesněji řečeno vizuálních) parametrů hran. Ovšem jakým způsobem se mění způsob vykreslení uzlů? Pokud je nutné u nějakého uzlu nastavit parametry vykreslování, je nutné takový uzel nejdříve deklarovat a teprve poté ho použít v grafu jako cíle hran. V dalším příkladu je ukázána explicitní deklarace tří uzlů s označením a, b a c. Povšimněte si, že je možné specifikovat jiný název uzlu, než odpovídá jeho označení (což je velmi užitečné, zejména u delších názvů, resp. popisků):
digraph {
splines="line"
a[label="start"]
b[color="red"]
c[color="blue"]
a -> b;
b -> c;
c -> d;
d -> a;
a -> a;
b -> b;
c -> c;
d -> d;
}
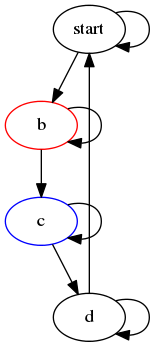
Obrázek 17: Graf, v němž mají jednotlivé uzly nastaven jiný vizuální styl vykreslování.
13. HTML entity v popiskách hran i uzlů
V popiskách grafů atd. lze používat Unicode znaky či HTML entity, které jsou vypsány například na stránce https://www.freeformatter.com/html-entities.html. V dalším příkladu jsou použity HTML entity, a to jak v popiskách uzlů, tak i v popiskách hran:
digraph {
rankdir=LR
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
a -> b[label="a → b", color="red", penwidth="2.0"];
b -> c[label="b → c", color="red", penwidth="2.0"];
c -> d;
d -> a;
a -> a[label="∞"]
b -> b[label="∞"]
c -> c[label="c → c", color="red", penwidth="2.0"];
d -> d[label="∞"]
}
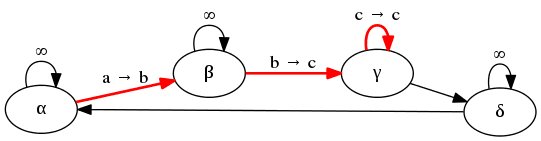
Obrázek 18: Graf s popisky, v nichž jsou použity HTML entity.
14. Graf se šesticí uzlů vykreslený nástrojem dot
V navazující kapitole se zmíníme o různých algoritmech určených pro rozmístění uzlů do grafu. Zaměříme se především na algoritmus-nástroj pojmenovaný circo, který uzly grafu umisťuje na pomyslnou kružnici. Pro otestování tohoto algoritmu bude použit tento graf se šesticí uzlů a hranami tvořícími cyklus:
digraph {
rankdir=LR
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
a -> b
b -> c
c -> d;
d -> e;
e -> f;
f -> a;
}
Základní nástroj dot takto definovaný graf vykreslí následovně:

Obrázek 19: Graf se šesticí uzlů cyklicky propojených orientovanými hranami vykreslený nástrojem dot.
15. Různé algoritmy pro rozmístění uzlů aneb praktická ukázka filozofie „rozděl a panuj“
Prozatím jsme všechny grafy vykreslovali nástrojem nazvaným dot. Ve skutečnosti je ovšem Graphviz sadou většího množství nástrojů, které se od sebe odlišují především tím, jaký algoritmus je použit pro rozmístění uzlů na ploše. Těchto nástrojů-algoritmů existuje celá řada a každý se hodí pro jiné účely:
| # | Název nástroje | Stručný popis |
|---|---|---|
| 1 | dot | používáno pro grafy s hierarchií uzlů a skupin |
| 2 | neato | symetrické grafy (typicky neorientované) |
| 3 | twopi | grafy, které mají uzly rozmístěny radiálně (paprskovitě) |
| 4 | circo | uzly rozmístěné na pomyslnou kružnizi |
| 5 | fdp | symetrické grafy |
| 6 | patchwork | typicky používáno pro stromy (tj. grafy bez cyklů) |
| 7 | osage | grafy s clustery (popíšeme si příště) |
16. Graf se šesticí uzlů vykreslený nástrojem circo
Opět se podívejme na definici grafu se šesticí uzlů, který obsahuje cyklus:
digraph {
rankdir=LR
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
a -> b
b -> c
c -> d;
d -> e;
e -> f;
f -> a;
}
V případě, že pro vykreslení tohoto grafu použijeme nástroj circo, bude výsledek vypadat následovně:
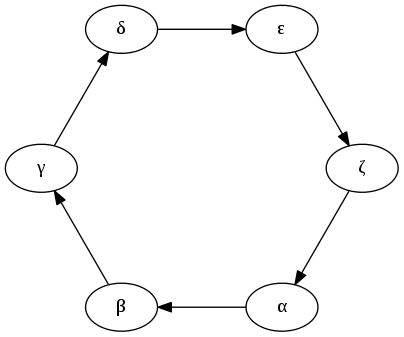
Obrázek 20: Graf se šesticí uzlů cyklicky propojených orientovanými hranami vykreslený nástrojem circo.
17. Další grafy vykreslené nástrojem circo
Podívejme se nyní na další grafy definované a popsané v předchozích kapitolách, ovšem nyní vykreslené nikoli nástrojem dot, ale nástrojem circo. Celkové rozmístění uzlů je – alespoň podle mého názoru – elegantnější:

Obrázek 21: Graf vykreslený nástrojem circo.

Obrázek 22: Graf vykreslený nástrojem circo.
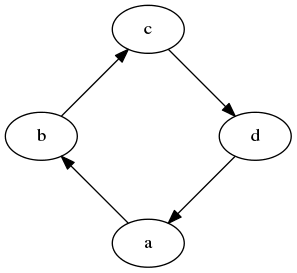
Obrázek 23: Graf vykreslený nástrojem circo.
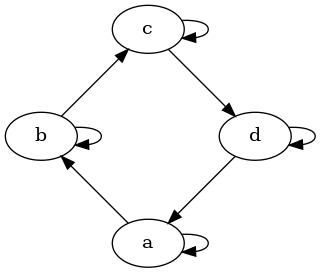
Obrázek 24: Graf vykreslený nástrojem circo.
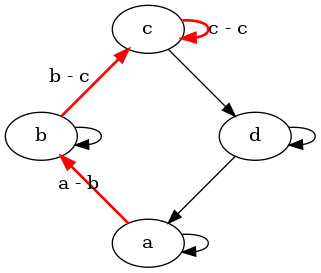
Obrázek 25: Graf vykreslený nástrojem circo.
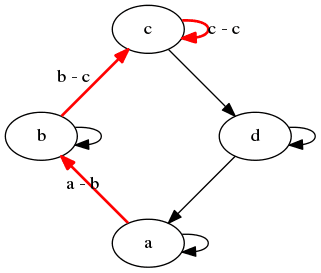
Obrázek 26: Graf vykreslený nástrojem circo.
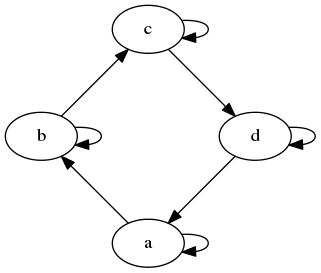
Obrázek 27: Graf vykreslený nástrojem circo.
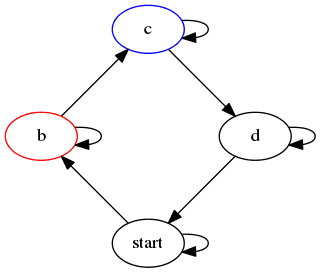
Obrázek 28: Graf vykreslený nástrojem circo.
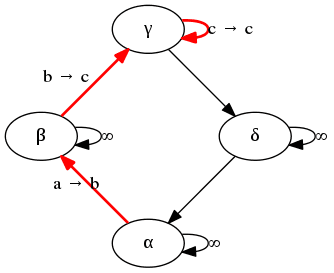
Obrázek 29: Graf vykreslený nástrojem circo.
18. Repositář s demonstračními příklady
Zdrojové kódy všech dnes použitých demonstračních příkladů byly uloženy do nového Git repositáře, který je dostupný na adrese https://github.com/tisnik/diagrams (stále na GitHubu :-). V případě, že nebudete chtít klonovat celý repositář (ten je ovšem – alespoň prozatím – velmi malý, dnes má přibližně jednotky kilobajtů), můžete namísto toho použít odkazy na jednotlivé demonstrační příklady, které naleznete v následující tabulce:
19. Odkazy na články s tématem programové tvorby grafů a diagramů
V této kapitole jsou uvedeny odkazy na předchozí články, v nichž jsme se zabývali tvorbou různých typů grafů a diagramů – a to v naprosté většině případů s využitím nějakého doménově specifického jazyka neboli DSL (Domain Specific Language), popř. nějakého univerzálního programovacího jazyka:
- Nástroje pro tvorbu UML diagramů
https://www.root.cz/clanky/nastroje-pro-tvorbu-uml-diagramu/ - Nástroje pro tvorbu UML diagramů z příkazové řádky
https://www.root.cz/clanky/nastroje-pro-tvorbu-uml-diagramu-z-prikazove-radky/ - Nástroje pro tvorbu UML diagramů z příkazové řádky (II)
https://www.root.cz/clanky/nastroje-pro-tvorbu-uml-diagramu-z-prikazove-radky-ii/ - Nástroje pro tvorbu grafů a diagramů z příkazové řádky
https://www.root.cz/clanky/nastroje-pro-tvorbu-grafu-a-diagramu-z-prikazove-radky/ - Sledování správy paměti v Pythonu s využitím nástroje objgraph
https://www.root.cz/clanky/sledovani-spravy-pameti-v-pythonu-s-vyuzitim-nastroje-objgraph/ - Programová tvorba diagramů v jazyku Clojure s využitím knihovny Rhizome
https://www.root.cz/clanky/programova-tvorba-diagramu-v-jazyku-clojure-s-vyuzitim-knihovny-rhizome/ - Tvorba sekvenčních diagramů v Pythonu s využitím knihovny Napkin
https://www.root.cz/clanky/tvorba-sekvencnich-diagramu-v-pythonu-s-vyuzitim-knihovny-napkin/ - Tvorba vývojových diagramů přímo ze zdrojových kódů Pythonu
https://www.root.cz/clanky/tvorba-vyvojovych-diagramu-primo-ze-zdrojovych-kodu-pythonu/ - Tvorba diagramů s architekturou systémů s využitím knihovny Diagrams
https://www.root.cz/clanky/tvorba-diagramu-s-architekturou-systemu-s-vyuzitim-knihovny-diagrams/ - Knihovny Diagrams a go-diagrams určené pro tvorbu diagramů s architekturou systémů
https://www.root.cz/clanky/knihovny-diagrams-a-go-diagrams-urcene-pro-tvorbu-diagramu-s-architekturou-systemu/
20. Odkazy na Internetu
- GraphViz Pocket Reference
https://graphs.grevian.org/example - Xfig home page
http://mcj.sourceforge.net/ - Xfig (Wikipedia)
https://en.wikipedia.org/wiki/Xfig - Xfig user manual
http://mcj.sourceforge.net/ - HTML Entity List
https://www.freeformatter.com/html-entities.html - Flowchart (Wikipedia)
https://en.wikipedia.org/wiki/Flowchart - DRAKON
https://en.wikipedia.org/wiki/DRAKON - Modeling language
https://en.wikipedia.org/wiki/Modeling_language - Napkin na GitHubu
https://github.com/pinetr2e/napkin - Napkin 0.6.8 na PyPi
https://pypi.org/project/napkin/ - PlantUML (home page)
http://plantuml.sourceforge.net/ - PlantUML (download page)
http://sourceforge.net/projects/plantuml/files/plantuml.jar/download - PlantUML (Language Reference Guide)
http://plantuml.sourceforge.net/PlantUML_Language_Reference_Guide.pdf - Rhizome
https://github.com/ztellman/rhizome - Swagger to UML
https://github.com/nlohmann/swagger_to_uml - pydiagrams
https://github.com/billingtonm/pydiagrams - graphviz(3) – Linux man page
https://linux.die.net/man/3/graphviz - dot(1) – Linux man page
https://linux.die.net/man/1/dot - neato(1) – Linux man page
https://linux.die.net/man/1/neato - twopi(1) – Linux man page
https://linux.die.net/man/1/twopi - circo(1) – Linux man page
https://linux.die.net/man/1/circo - fdp(1) – Linux man page
https://linux.die.net/man/1/fdp - sfdp(1) – Linux man page
https://linux.die.net/man/1/sfdp - Plain-text diagrams take shape in Asciidoctor!
http://asciidoctor.org/news/2014/02/18/plain-text-diagrams-in-asciidoctor/ - Graphviz – Graph Visualization Software
http://www.graphviz.org/ - graphviz (Manual Page)
http://www.root.cz/man/7/graphviz/ - dot (Manual page)
http://www.root.cz/man/1/dot/ - dot (Manual v PDF)
https://graphviz.org/pdf/dot.1.pdf - Ditaa home page
http://ditaa.sourceforge.net/ - Ditaa introduction
http://ditaa.sourceforge.net/#intro - Ditaa usage
http://ditaa.sourceforge.net/#usage - Node, Edge and Graph Attributes
http://www.graphviz.org/doc/info/attrs.html - Graphviz (Wikipedia)
http://en.wikipedia.org/wiki/Graphviz - Unified Modeling Language
https://en.wikipedia.org/wiki/Unified_Modeling_Language - UML basics: The sequence diagram
http://www.ibm.com/developerworks/rational/library/3101.html - UML 2 State Machine Diagrams: An Agile Introduction
http://www.agilemodeling.com/artifacts/stateMachineDiagram.htm - Sequence diagram (Wikipedia)
https://en.wikipedia.org/wiki/Sequence_diagram - UML 2 Sequence Diagrams: An Agile Introduction
http://www.agilemodeling.com/artifacts/sequenceDiagram.htm - A Quick Introduction to UML Sequence Diagrams
http://www.tracemodeler.com/articles/a_quick_introduction_to_uml_sequence_diagrams/ - UML Sequence Diagrams
https://www.uml-diagrams.org/sequence-diagrams.html - Web Sequence Diagrams
https://www.websequencediagrams.com/ - Drawing sequence diagrams “napkin style”
https://modeling-languages.com/drawing-sequence-diagrams-napkin-style/ - Curated list of UML tools – 2020 edition
https://modeling-languages.com/uml-tools/#textual - Flowchart diagrams vs. UML activity diagrams
https://stackoverflow.com/questions/7081215/flowchart-diagrams-vs-uml-activity-diagrams - Kopenograms – Graphical Language for Structured Algorithms
https://kopenogram.org/Assets/Kopenograms_Graphical_Language_for_Structured_Algorithms.pdf - Kopenograms and Their Implementation in BlueJ
https://link.springer.com/chapter/10.1007%2F978–3–319–46535–7_8 - The simplest way to describe your flows
https://code2flow.com/ - Allan Mogensen and his Legacy
http://www.worksimp.com/articles/allan-mogensen.htm - Diagrams: Diagram as Code
https://diagrams.mingrammer.com/ - Diagrams: Guides
https://diagrams.mingrammer.com/docs/guides/diagram - Diagrams: Nodes
https://diagrams.mingrammer.com/docs/nodes/onprem - go-diagrams
https://github.com/blushft/go-diagrams - GoJS
https://gojs.net/latest/index.html - Code visualization: How to turn complex code into diagrams
https://www.lucidchart.com/blog/visualize-code-documentation - Create dependency diagrams from your code
https://docs.microsoft.com/en-us/visualstudio/modeling/create-layer-diagrams-from-your-code?view=vs-2019 - Software Architecture Diagrams as Code
https://shekhargulati.com/2020/04/21/software-architecture-diagrams-as-code/ - Processing spreadsheet data in Go
https://appliedgo.net/spreadsheet/ - Stránka projektu plotly
https://plot.ly/ - Plotly JavaScript Open Source Graphing Library
https://plot.ly/javascript/ - Domain coloring
https://en.wikipedia.org/wiki/Domain_coloring - The Gonum Numerical Computing Package
https://www.gonum.org/post/introtogonum/ - Gomacro na GitHubu
https://github.com/cosmos72/gomacro - gophernotes – Use Go in Jupyter notebooks and nteract
https://github.com/gopherdata/gophernotes - gonum
https://github.com/gonum - go-gota/gota – DataFrames and data wrangling in Go (Golang)
https://porter.io/github.com/go-gota/gota - A repository for plotting and visualizing data
https://github.com/gonum/plot - Gonum Numerical Packages
https://www.gonum.org/ - Getting started with Go modules
https://medium.com/@fonseka.live/getting-started-with-go-modules-b3dac652066d - Create projects independent of $GOPATH using Go Modules
https://medium.com/mindorks/create-projects-independent-of-gopath-using-go-modules-802260cdfb51o - Anatomy of Modules in Go
https://medium.com/rungo/anatomy-of-modules-in-go-c8274d215c16 - Modules
https://github.com/golang/go/wiki/Modules - Go Modules Tutorial
https://tutorialedge.net/golang/go-modules-tutorial/ - Module support
https://golang.org/cmd/go/#hdr-Module_support - Go vs. Python
https://www.peterbe.com/plog/govspy - PackageManagementTools
https://github.com/golang/go/wiki/PackageManagementTools




































