Obsah
1. Využití různých algoritmů pro rozmístění uzlů na plochu obrázku
2. Graf se šesticí uzlů spojených jediným cyklem
3. Výsledek aplikace jednotlivých algoritmů
4. Neorientovaný graf se středovým uzlem
5. Výsledek aplikace jednotlivých algoritmů
6. Explicitní specifikace kořenového uzlu
7. Graf se středovým uzlem a okrajovými podstromy
8. Algoritmy dot a circo a několikanásobné hrany mezi uzly
9. Symetrický orientovaný i neorientovaný graf s podstromy
11. Postupné přidávání podgrafů
12. Barevné zvýraznění podgrafů
13. Postupné přidávání podgrafů „clusterX“ se specifikací jejich barevné výplně
14. Změna tvaru uzlů v grafech
17. Repositář s demonstračními příklady
18. Odkazy na články s tématem programové tvorby grafů a diagramů
1. Využití různých algoritmů pro rozmístění uzlů na plochu obrázku
Na úvodní článek o nástroji Graphviz dnes navážeme a popíšeme si další možnosti, které tento nástroj (resp. přesněji řečeno sada nástrojů) uživatelům nabízí. Nejprve se zaměříme na různé algoritmy určené pro rozmístění uzlů na ploše grafu. Následně se budeme zabývat problematikou specifikace i vizuálního zvýraznění podgrafů. A ve třetí části článku si ukážeme, jak lze měnit tvar uzlů popř. tvar šipek či celých hran.
Prozatím jsme většinu grafů vykreslovali nástrojem nazvaným dot (což je současně i jméno jazyka pro definici grafů). Ve skutečnosti je ovšem Graphviz sadou většího množství nástrojů, které se od sebe odlišují především tím, jaký algoritmus je použit pro rozmístění uzlů na ploše – což do značné míry ovlivňuje přehlednost (či naopak nepřehlednost) vykresleného grafu. Těchto nástrojů-algoritmů existuje celá řada a každý se hodí pro jiné účely. Standardní algoritmy dostupné v instalaci Graphviz jsou vypsány v tabulce pod tímto odstavcem:
| # | Název nástroje | Stručný popis |
|---|---|---|
| 1 | dot | používáno pro grafy s hierarchií uzlů a skupin (podgrafy, clustery) |
| 2 | neato | určeno pro symetrické grafy (typicky neorientované) |
| 3 | twopi | určeno pro grafy, které mají uzly rozmístěny radiálně (paprskovitě) |
| 4 | circo | určeno pro uzly rozmístěnými na pomyslnou kružnici |
| 5 | fdp | určeno především pro symetrické grafy |
| 6 | sfdp | určeno především pro rozsáhlé neorientované grafy |
| 7 | patchwork | typicky používáno pro stromy (tj. pro grafy bez cyklů) |
| 8 | osage | určeno pro grafy s clustery, alternativa k dot |
Vliv jednotlivých algoritmů si ukážeme na několika příkladech s různými typy grafů.
2. Graf se šesticí uzlů spojených jediným cyklem
Prvním demonstračním příkladem, s nímž se dnes seznámíme, je příklad obsahující definici grafu se šesticí uzlů, které jsou propojeny jediným cyklem. Konkrétně to znamená, že první uzel je propojen s uzlem druhým, ten s uzlem třetím atd. až poslední uzel je opět propojen s prvním uzlem. Jedná se o neorientovaný graf:
graph {
rankdir=LR
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
a -- b
b -- c
c -- d;
d -- e;
e -- f;
f -- a;
}
3. Výsledek aplikace jednotlivých algoritmů

Obrázek 1: Algoritmus circo.

Obrázek 2: Algoritmus dot.

Obrázek 3: Algoritmus fdp.

Obrázek 4: Algoritmus neato.

Obrázek 5: Algoritmus osage.

Obrázek 6: Algoritmus patchwork.

Obrázek 7: Algoritmus sfpd.

Obrázek 8: Algoritmus twopi.
4. Neorientovaný graf se středovým uzlem
Ve druhém grafu, na němž budeme testovat různé algoritmy pro rozložení uzlů, přidáme „středový“ uzel o s popiskem ω. Tento uzel je propojen se všemi ostatními uzly (a ty jsou navzájem propojeny stejně, jako tomu bylo v prvním demonstračním příkladu):
graph {
rankdir=LR
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
o[label="ω"]
a -- b
b -- c
c -- d;
d -- e;
e -- f;
f -- a;
a -- o;
b -- o;
c -- o;
d -- o;
e -- o;
f -- o;
}
5. Výsledek aplikace jednotlivých algoritmů

Obrázek 9: Algoritmus circo.

Obrázek 10: Algoritmus dot.

Obrázek 11: Algoritmus fdp.

Obrázek 12: Algoritmus neato.

Obrázek 13: Algoritmus osage.

Obrázek 14: Algoritmus patchwork.
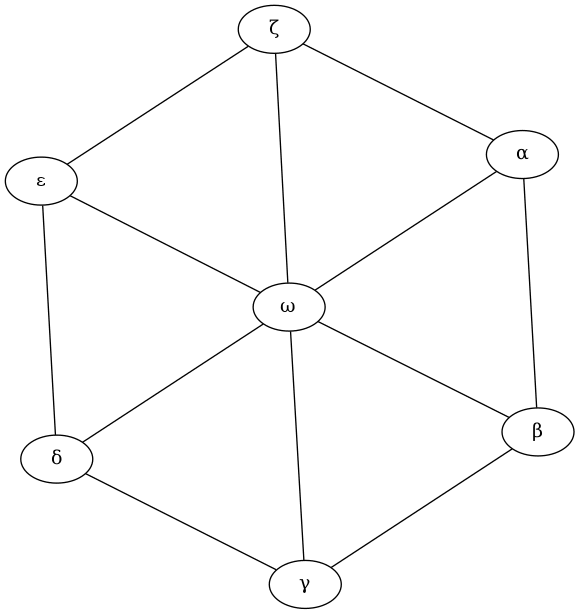
Obrázek 15: Algoritmus sfpd.

Obrázek 16: Algoritmus twopi.
6. Explicitní specifikace kořenového uzlu
Algoritmus twopi vyžaduje explicitní specifikaci kořenového uzlu. Pokud neví, který uzel je kořenový, vybere náhodně libovolný uzel, takže pravděpodobnost, že vybere ten správný, je relativně malá (a nelze se na ni spoléhat). Z tohoto důvodu je možné v jazyce dot specifikovat kořenový uzel atributem root. Tento kořenový uzel bude umístěn uprostřed grafu a ostatní uzly se uspořádají do soustředných kružnic. Předchozí demonstrační příklad tedy postačuje nepatrně upravit:
graph {
rankdir=LR
root=o
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
o[label="ω"]
a -- b
b -- c
c -- d;
d -- e;
e -- f;
f -- a;
a -- o;
b -- o;
c -- o;
d -- o;
e -- o;
f -- o;
}
Z výsledku je nyní patrné, že algoritmus twopi vytvořil estetický symetrický graf:

Obrázek 17: Výsledek práce algoritmu twopi.
7. Graf se středovým uzlem a okrajovými podstromy
V předchozích kapitolách jsme si řekli, že se algoritmus twopi snaží umístit jeden uzel do středu grafu a ostatní uzly do soustředných kružnic okolo něj. Na sedmnáctém obrázku je patrné použití jediné pomyslné kružnice, ovšem v případě složitějších grafů je možné mít těchto kružnic více. Toto chování algoritmu twopi si ukážeme na dalším grafu, jenž má (opět) explicitně zvolený středový uzel (kořenový). Z dalších šesti základních uzlů vedou hrany do dalších dvanácti uzlů:
graph {
rankdir=LR
root=o
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
o[label="ω"]
a -- b;
b -- c;
c -- d;
d -- e;
e -- f;
f -- a;
a -- o;
b -- o;
c -- o;
d -- o;
e -- o;
f -- o;
a -- a1;
a -- a2;
b -- b1;
b -- b2;
c -- c1;
c -- c2;
d -- d1;
d -- d2;
e -- e1;
e -- e2;
f -- f1;
f -- f2;
}
Takto definovaný graf se s využitím algoritmu twopi zobrazí následovně:

Obrázek 18: Výsledek práce algoritmu twopi.
8. Algoritmy dot a circo a několikanásobné hrany mezi uzly
Mnohdy je nutné pracovat s grafy, v nichž jsou uzly propojeny několikanásobnými hranami (ať již orientovanými, tak i neorientovanými). Takové grafy jsou zpracovatelné všemi osmi výše zmíněnými algoritmy, ovšem s různých úspěchem. Ukažme si nyní, co se stane, pokud do grafu z předchozí kapitoly přidáme hrany mezi základní šestici uzlů α až ζ:
graph {
rankdir=LR
root=o
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
o[label="ω"]
a -- b;
b -- c;
c -- d;
d -- e;
e -- f;
f -- a;
a -- b;
b -- c;
c -- d;
d -- e;
e -- f;
f -- a;
a -- o;
b -- o;
c -- o;
d -- o;
e -- o;
f -- o;
a -- a1;
a -- a2;
b -- b1;
b -- b2;
c -- c1;
c -- c2;
d -- d1;
d -- d2;
e -- e1;
e -- e2;
f -- f1;
f -- f2;
}
Základní algoritmus dot i přes snahu vytvořil dosti nečitelný graf:

Obrázek 19: Výsledek práce algoritmu dot.
Naproti tomu algoritmus twopi vytvořil graf, který je mnohem lepší jak po stránce vizuální, tak i z hlediska celkové čitelnosti:

Obrázek 20: Výsledek práce algoritmu twopi.
9. Symetrický orientovaný i neorientovaný graf s podstromy
Algoritmus circo dokáže zpracovat jak orientované, tak i neorientované grafy. Můžeme se o tom ostatně velmi snadno přesvědčit po vykreslení grafů definovaných v následující dvojici demonstračních příkladů. První z těchto příkladů je neorientovaným grafem se šesti uzly tvořícími cyklus a s dalšími dvanácti listy:
graph {
rankdir=LR
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
a -- b;
b -- c;
c -- d;
d -- e;
e -- f;
f -- a;
a -- b;
b -- c;
c -- d;
d -- e;
e -- f;
f -- a;
a -- a1;
a -- a2;
b -- b1;
b -- b2;
c -- c1;
c -- c2;
d -- d1;
d -- d2;
e -- e1;
e -- e2;
f -- f1;
f -- f2;
}
Druhý demonstrační příklad z této kapitoly je prakticky totožný, ovšem graf je nyní orientovaný – jeho hrany jsou tedy tvořeny šipkami:
digraph {
rankdir=LR
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
a -> b;
b -> c;
c -> d;
d -> e;
e -> f;
f -> a;
b -> a;
c -> b;
d -> c;
e -> d;
f -> e;
a -> f;
a -> a1;
a -> a2;
b -> b1;
b -> b2;
c -> c1;
c -> c2;
d -> d1;
d -> d2;
e -> e1;
e -> e2;
f -> f1;
f -> f2;
}
Z následující dvojice obrázků je patrné, že vykreslené grafy jsou prakticky totožné (pochopitelně až na odlišné hrany):

Obrázek 21: Výsledek práce algoritmu circo (neorientovaný graf).

Obrázek 22: Výsledek práce algoritmu circo (orientovaný graf).
10. Specifikace podgrafů
Doménově specifický jazyk dot umožňuje v grafu definovat podgrafy, což jsou uzly, které mohou mít společné vlastnosti (a to i vizuální). Pokud nějaké uzly tvoří podgraf, budou se jednotlivé algoritmy snažit takové uzly vhodným způsobem uspořádat. Samotná definice podgrafu vypadá následovně:
...
...
...
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
subgraph {
rank = same;
a;
a1;
a2;
}
...
...
...
Z tohoto úryvku kódu je patrné, že v podgrafu můžeme pouze specifikovat uzly, které do něj patří.
11. Postupné přidávání podgrafů
Ukažme si nyní, jak existence podgrafů ovlivňuje způsob zobrazení grafu. Začneme s následujícím grafem (s celkem osmnácti uzly), v němž žádné podgrafy definovány nejsou:
digraph {
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
a -> b;
b -> c;
c -> d;
d -> e;
e -> f;
f -> a;
b -> a;
c -> b;
d -> c;
e -> d;
f -> e;
a -> f;
a -> a1;
a -> a2;
b -> b1;
b -> b2;
c -> c1;
c -> c2;
d -> d1;
d -> d2;
e -> e1;
e -> e2;
f -> f1;
f -> f2;
}
Přidáme první podgraf:
digraph {
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
subgraph {
rank = same;
a;
a1;
a2;
}
a -> b;
b -> c;
c -> d;
d -> e;
e -> f;
f -> a;
b -> a;
c -> b;
d -> c;
e -> d;
f -> e;
a -> f;
a -> a1;
a -> a2;
b -> b1;
b -> b2;
c -> c1;
c -> c2;
d -> d1;
d -> d2;
e -> e1;
e -> e2;
f -> f1;
f -> f2;
}
Přidáme druhý podgraf:
digraph {
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
subgraph {
rank = same;
a;
a1;
a2;
}
subgraph {
rank = same;
b;
b1;
b2;
}
a -> b;
b -> c;
c -> d;
d -> e;
e -> f;
f -> a;
b -> a;
c -> b;
d -> c;
e -> d;
f -> e;
a -> f;
a -> a1;
a -> a2;
b -> b1;
b -> b2;
c -> c1;
c -> c2;
d -> d1;
d -> d2;
e -> e1;
e -> e2;
f -> f1;
f -> f2;
}
Přidáme třetí podgraf:
digraph {
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
subgraph {
rank = same;
a;
a1;
a2;
}
subgraph {
rank = same;
b;
b1;
b2;
}
subgraph {
rank = same;
c;
c1;
c2;
}
a -> b;
b -> c;
c -> d;
d -> e;
e -> f;
f -> a;
b -> a;
c -> b;
d -> c;
e -> d;
f -> e;
a -> f;
a -> a1;
a -> a2;
b -> b1;
b -> b2;
c -> c1;
c -> c2;
d -> d1;
d -> d2;
e -> e1;
e -> e2;
f -> f1;
f -> f2;
}
Přidáme čtvrtý podgraf:
digraph {
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
subgraph {
rank = same;
a;
a1;
a2;
}
subgraph {
rank = same;
b;
b1;
b2;
}
subgraph {
rank = same;
c;
c1;
c2;
}
subgraph {
rank = same;
d;
d1;
d2;
}
a -> b;
b -> c;
c -> d;
d -> e;
e -> f;
f -> a;
b -> a;
c -> b;
d -> c;
e -> d;
f -> e;
a -> f;
a -> a1;
a -> a2;
b -> b1;
b -> b2;
c -> c1;
c -> c2;
d -> d1;
d -> d2;
e -> e1;
e -> e2;
f -> f1;
f -> f2;
}
Přidáme pátý (předposlední) podgraf:
digraph {
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
subgraph {
rank = same;
a;
a1;
a2;
}
subgraph {
rank = same;
b;
b1;
b2;
}
subgraph {
rank = same;
c;
c1;
c2;
}
subgraph {
rank = same;
d;
d1;
d2;
}
subgraph {
rank = same;
e;
e1;
e2;
}
a -> b;
b -> c;
c -> d;
d -> e;
e -> f;
f -> a;
b -> a;
c -> b;
d -> c;
e -> d;
f -> e;
a -> f;
a -> a1;
a -> a2;
b -> b1;
b -> b2;
c -> c1;
c -> c2;
d -> d1;
d -> d2;
e -> e1;
e -> e2;
f -> f1;
f -> f2;
}
A konečně přidáme šestý (poslední) podgraf:
digraph {
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
subgraph {
rank = same;
a;
a1;
a2;
}
subgraph {
rank = same;
b;
b1;
b2;
}
subgraph {
rank = same;
c;
c1;
c2;
}
subgraph {
rank = same;
d;
d1;
d2;
}
subgraph {
rank = same;
e;
e1;
e2;
}
subgraph {
rank = same;
f;
f1;
f2;
}
a -> b;
b -> c;
c -> d;
d -> e;
e -> f;
f -> a;
b -> a;
c -> b;
d -> c;
e -> d;
f -> e;
a -> f;
a -> a1;
a -> a2;
b -> b1;
b -> b2;
c -> c1;
c -> c2;
d -> d1;
d -> d2;
e -> e1;
e -> e2;
f -> f1;
f -> f2;
}
Výsledky jsou pro lepší vizuální porovnání zobrazeny pod sebou:

Obrázek 23: Graf bez podgrafů.

Obrázek 24: Graf s jedním podgrafem.

Obrázek 25: Graf se dvěma podgrafy.

Obrázek 26: Graf se třemi podgrafy.

Obrázek 27: Graf se čtyřmi podgrafy.

Obrázek 28: Graf s pěti podgrafy.

Obrázek 29: Graf se šesti podgrafy.
12. Barevné zvýraznění podgrafů
V desáté kapitole jsme si řekli, že podgrafy je možné pojmenovat:
subgraph totoJeJmeno {
rank = same;
a;
a1;
a2;
}
V případě, že jméno podgrafu začíná slovem „cluster“, bude podgraf orámován. A nejen to – bude možné specifikovat i barvu výplně tohoto orámování. Následuje příklad využití této velmi užitečné vlastnosti doménově specifického jazyka dot:
subgraph cluster1 {
rank = same;
style = "filled";
fillcolor = "#80ff80";
a;
a1;
a2;
}
13. Postupné přidávání podgrafů „clusterX“ se specifikací jejich barevné výplně
Podobně jako v jedenácté kapitole se i nyní pokusíme o postupné přidávání podgrafů se jménem „clusterX“ (za X je dosazeno kladné celé číslo) do definice grafu a následně zkontrolujeme, jak vypadají výsledky po vykreslení grafu.
Začneme s následujícím grafem (s celkem osmnácti uzly), v němž žádné podgrafy definovány nejsou:
digraph {
rankdir=LR
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
a -> b;
b -> c;
c -> d;
d -> e;
e -> f;
f -> a;
b -> a;
c -> b;
d -> c;
e -> d;
f -> e;
a -> f;
a -> a1;
a -> a2;
b -> b1;
b -> b2;
c -> c1;
c -> c2;
d -> d1;
d -> d2;
e -> e1;
e -> e2;
f -> f1;
f -> f2;
}
Přidáme první podgraf:
digraph {
rankdir=LR
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
subgraph cluster1 {
rank = same;
style = "filled";
fillcolor = "#80ff80";
a;
a1;
a2;
}
a -> b;
b -> c;
c -> d;
d -> e;
e -> f;
f -> a;
b -> a;
c -> b;
d -> c;
e -> d;
f -> e;
a -> f;
a -> a1;
a -> a2;
b -> b1;
b -> b2;
c -> c1;
c -> c2;
d -> d1;
d -> d2;
e -> e1;
e -> e2;
f -> f1;
f -> f2;
}
Přidáme druhý podgraf:
digraph {
rankdir=LR
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
subgraph cluster1 {
rank = same;
style = "filled";
fillcolor = "#80ff80";
a;
a1;
a2;
}
subgraph cluster2 {
rank = same;
style = "filled";
fillcolor = "#80ffff";
b;
b1;
b2;
}
a -> b;
b -> c;
c -> d;
d -> e;
e -> f;
f -> a;
b -> a;
c -> b;
d -> c;
e -> d;
f -> e;
a -> f;
a -> a1;
a -> a2;
b -> b1;
b -> b2;
c -> c1;
c -> c2;
d -> d1;
d -> d2;
e -> e1;
e -> e2;
f -> f1;
f -> f2;
}
Přidáme třetí podgraf:
digraph {
rankdir=LR
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
subgraph cluster1 {
rank = same;
style = "filled";
fillcolor = "#80ff80";
a;
a1;
a2;
}
subgraph cluster2 {
rank = same;
style = "filled";
fillcolor = "#80ffff";
b;
b1;
b2;
}
subgraph cluster3 {
rank = same;
style = "filled";
fillcolor = "#8080ff";
c;
c1;
c2;
}
a -> b;
b -> c;
c -> d;
d -> e;
e -> f;
f -> a;
b -> a;
c -> b;
d -> c;
e -> d;
f -> e;
a -> f;
a -> a1;
a -> a2;
b -> b1;
b -> b2;
c -> c1;
c -> c2;
d -> d1;
d -> d2;
e -> e1;
e -> e2;
f -> f1;
f -> f2;
}
Přidáme čtvrtý podgraf:
digraph {
rankdir=LR
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
subgraph cluster1 {
rank = same;
style = "filled";
fillcolor = "#80ff80";
a;
a1;
a2;
}
subgraph cluster2 {
rank = same;
style = "filled";
fillcolor = "#80ffff";
b;
b1;
b2;
}
subgraph cluster3 {
rank = same;
style = "filled";
fillcolor = "#8080ff";
c;
c1;
c2;
}
subgraph cluster4 {
rank = same;
style = "filled";
fillcolor = "#ff80ff";
d;
d1;
d2;
}
a -> b;
b -> c;
c -> d;
d -> e;
e -> f;
f -> a;
b -> a;
c -> b;
d -> c;
e -> d;
f -> e;
a -> f;
a -> a1;
a -> a2;
b -> b1;
b -> b2;
c -> c1;
c -> c2;
d -> d1;
d -> d2;
e -> e1;
e -> e2;
f -> f1;
f -> f2;
}
Přidáme pátý (předposlední) podgraf:
digraph {
rankdir=LR
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
subgraph cluster1 {
rank = same;
style = "filled";
fillcolor = "#80ff80";
a;
a1;
a2;
}
subgraph cluster2 {
rank = same;
style = "filled";
fillcolor = "#80ffff";
b;
b1;
b2;
}
subgraph cluster3 {
rank = same;
style = "filled";
fillcolor = "#8080ff";
c;
c1;
c2;
}
subgraph cluster4 {
rank = same;
style = "filled";
fillcolor = "#ff80ff";
d;
d1;
d2;
}
subgraph cluster5 {
rank = same;
style = "filled";
fillcolor = "#ff8080";
e;
e1;
e2;
}
a -> b;
b -> c;
c -> d;
d -> e;
e -> f;
f -> a;
b -> a;
c -> b;
d -> c;
e -> d;
f -> e;
a -> f;
a -> a1;
a -> a2;
b -> b1;
b -> b2;
c -> c1;
c -> c2;
d -> d1;
d -> d2;
e -> e1;
e -> e2;
f -> f1;
f -> f2;
}
A konečně přidáme šestý (poslední) podgraf:
digraph {
rankdir=LR
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
subgraph cluster1 {
rank = same;
style = "filled";
fillcolor = "#80ff80";
a;
a1;
a2;
}
subgraph cluster2 {
rank = same;
style = "filled";
fillcolor = "#80ffff";
b;
b1;
b2;
}
subgraph cluster3 {
rank = same;
style = "filled";
fillcolor = "#8080ff";
c;
c1;
c2;
}
subgraph cluster4 {
rank = same;
style = "filled";
fillcolor = "#ff80ff";
d;
d1;
d2;
}
subgraph cluster5 {
rank = same;
style = "filled";
fillcolor = "#ff8080";
e;
e1;
e2;
}
subgraph cluster6 {
rank = same;
style = "filled";
fillcolor = "#ffff80";
f;
f1;
f2;
}
a -> b;
b -> c;
c -> d;
d -> e;
e -> f;
f -> a;
b -> a;
c -> b;
d -> c;
e -> d;
f -> e;
a -> f;
a -> a1;
a -> a2;
b -> b1;
b -> b2;
c -> c1;
c -> c2;
d -> d1;
d -> d2;
e -> e1;
e -> e2;
f -> f1;
f -> f2;
}
Výsledky jsou pro lepší vizuální porovnání zobrazeny pod sebou:

Obrázek 30: Graf bez podgrafů.

Obrázek 31: Graf s jedním podgrafem (clusterem).

Obrázek 32: Graf se dvěma podgrafy (clustery).

Obrázek 33: Graf se třemi podgrafy (clustery).

Obrázek 34: Graf se čtyřmi podgrafy (clustery).

Obrázek 35: Graf s pěti podgrafy (clustery).
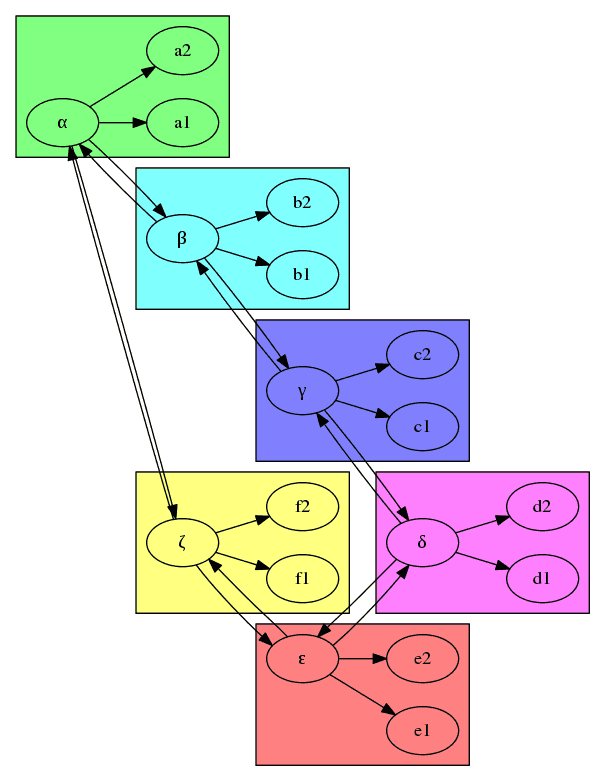
Obrázek 36: Graf se šesti podgrafy (clustery).
14. Změna tvaru uzlů v grafech
S využitím atributu shape je možné měnit tvar uzlů v grafech. Opět si tuto funkcionalitu ukažme na několika demonstračních příkladech. Začneme grafem se standardními tvary uzlů:
graph {
rankdir=LR
a[label="α"]
b[label="β"]
c[label="γ"]
d[label="δ"]
e[label="ε"]
f[label="ζ"]
a -- b
b -- c
c -- d;
d -- e;
e -- f;
f -- a;
}

Obrázek 37: Graf se standardními tvary uzlů.
Ve druhém příkladu jsou všechny uzly upraveny tak, aby se vždy zobrazily jako kružnice a nikoli jako elipsy:
graph {
rankdir=LR
a[shape="circle", label="α"]
b[shape="circle", label="β"]
c[shape="circle", label="γ"]
d[shape="circle", label="δ"]
e[shape="circle", label="ε"]
f[shape="circle", label="ζ"]
a -- b
b -- c
c -- d;
d -- e;
e -- f;
f -- a;
}

Obrázek 38: Graf s uzly ve tvaru kružnice.
A konečně ve třetím grafu jsou všechny uzly zobrazeny obdélníkem:
graph {
rankdir=LR
a[shape="box", label="α"]
b[shape="box", label="β"]
c[shape="box", label="γ"]
d[shape="box", label="δ"]
e[shape="box", label="ε"]
f[shape="box", label="ζ"]
a -- b
b -- c
c -- d;
d -- e;
e -- f;
f -- a;
}

Obrázek 39: Graf s uzly ve tvaru obdélníku.
15. Tvary šipek
I tvary šipek (tedy ukončení hran) je možné modifikovat. Styl šipky lze pojmenovat, stejně jako styl uzlu, nebo (což je častější) je možné styl určit přímo u definice hrany. A právě tuto druhou možnost si ukážeme v dalším demonstračním příkladu s orientovaným grafem, v němž je definováno osm hran, každá s odlišným stylem šipky:
digraph {
splines="line"
a[label="start"]
b[color="red"]
c[color="blue"]
a -> b [arrowhead=box];
b -> c [arrowhead=crow];
c -> d [arrowhead=curve];
d -> a [arrowhead=icurve];
b -> a [arrowhead=diamond];
c -> b [arrowhead=dot];
d -> c [arrowhead=tee];
d -> a [arrowhead=vee];
}

Obrázek 40: Orientovaný graf s různými styly konců hran.
16. Obsah navazujícího článku
Ve třetím článku o nástroji Graphviz si ukážeme další pomocné nástroje – hledání cest, zvýraznění automaticky nalezeného podgrafu atd. Taktéž si popíšeme některé užitečné nástroje, které jsou nad Graphviz postaveny. Příkladem může být projekt schemaSpy určený pro vizualizaci schématu relační databáze.

Obrázek 41: Výsledek činnosti nástroje schemaSpy.
17. Repositář s demonstračními příklady
Zdrojové kódy všech dnes použitých demonstračních příkladů byly uloženy do nového Git repositáře, který je dostupný na adrese https://github.com/tisnik/diagrams (stále na GitHubu :-). V případě, že nebudete chtít klonovat celý repositář (ten je ovšem – alespoň prozatím – velmi malý, dnes má přibližně jednotky kilobajtů), můžete namísto toho použít odkazy na jednotlivé demonstrační příklady, které naleznete v následující tabulce:
18. Odkazy na články s tématem programové tvorby grafů a diagramů
V této kapitole jsou uvedeny odkazy na předchozí články, v nichž jsme se zabývali tvorbou různých typů grafů a diagramů – a to v naprosté většině případů s využitím nějakého doménově specifického jazyka neboli DSL (Domain Specific Language) popř. nějakého univerzálního programovacího jazyka (zejména Python, Go, Clojure):
- Nástroje pro tvorbu UML diagramů
https://www.root.cz/clanky/nastroje-pro-tvorbu-uml-diagramu/ - Nástroje pro tvorbu UML diagramů z příkazové řádky
https://www.root.cz/clanky/nastroje-pro-tvorbu-uml-diagramu-z-prikazove-radky/ - Nástroje pro tvorbu UML diagramů z příkazové řádky (II)
https://www.root.cz/clanky/nastroje-pro-tvorbu-uml-diagramu-z-prikazove-radky-ii/ - Nástroje pro tvorbu grafů a diagramů z příkazové řádky
https://www.root.cz/clanky/nastroje-pro-tvorbu-grafu-a-diagramu-z-prikazove-radky/ - Sledování správy paměti v Pythonu s využitím nástroje objgraph
https://www.root.cz/clanky/sledovani-spravy-pameti-v-pythonu-s-vyuzitim-nastroje-objgraph/ - Programová tvorba diagramů v jazyku Clojure s využitím knihovny Rhizome
https://www.root.cz/clanky/programova-tvorba-diagramu-v-jazyku-clojure-s-vyuzitim-knihovny-rhizome/ - Tvorba sekvenčních diagramů v Pythonu s využitím knihovny Napkin
https://www.root.cz/clanky/tvorba-sekvencnich-diagramu-v-pythonu-s-vyuzitim-knihovny-napkin/ - Tvorba vývojových diagramů přímo ze zdrojových kódů Pythonu
https://www.root.cz/clanky/tvorba-vyvojovych-diagramu-primo-ze-zdrojovych-kodu-pythonu/ - Tvorba diagramů s architekturou systémů s využitím knihovny Diagrams
https://www.root.cz/clanky/tvorba-diagramu-s-architekturou-systemu-s-vyuzitim-knihovny-diagrams/ - Knihovny Diagrams a go-diagrams určené pro tvorbu diagramů s architekturou systémů
https://www.root.cz/clanky/knihovny-diagrams-a-go-diagrams-urcene-pro-tvorbu-diagramu-s-architekturou-systemu/ - Tvorba grafů a diagramů s využitím doménově specifického jazyka nástroje Graphviz
https://www.root.cz/clanky/tvorba-grafu-a-diagramu-s-vyuzitim-domenove-specifickeho-jazyka-nastroje-graphviz/
19. Odkazy na Internetu
- GraphViz Pocket Reference
https://graphs.grevian.org/example - Xfig home page
http://mcj.sourceforge.net/ - Xfig (Wikipedia)
https://en.wikipedia.org/wiki/Xfig - Xfig user manual
http://mcj.sourceforge.net/ - HTML Entity List
https://www.freeformatter.com/html-entities.html - Flowchart (Wikipedia)
https://en.wikipedia.org/wiki/Flowchart - DRAKON
https://en.wikipedia.org/wiki/DRAKON - Modeling language
https://en.wikipedia.org/wiki/Modeling_language - Napkin na GitHubu
https://github.com/pinetr2e/napkin - Napkin 0.6.8 na PyPi
https://pypi.org/project/napkin/ - PlantUML (home page)
http://plantuml.sourceforge.net/ - PlantUML (download page)
http://sourceforge.net/projects/plantuml/files/plantuml.jar/download - PlantUML (Language Reference Guide)
http://plantuml.sourceforge.net/PlantUML_Language_Reference_Guide.pdf - Rhizome
https://github.com/ztellman/rhizome - Swagger to UML
https://github.com/nlohmann/swagger_to_uml - pydiagrams
https://github.com/billingtonm/pydiagrams - graphviz(3) – Linux man page
https://linux.die.net/man/3/graphviz - dot(1) – Linux man page
https://linux.die.net/man/1/dot - neato(1) – Linux man page
https://linux.die.net/man/1/neato - twopi(1) – Linux man page
https://linux.die.net/man/1/twopi - circo(1) – Linux man page
https://linux.die.net/man/1/circo - fdp(1) – Linux man page
https://linux.die.net/man/1/fdp - sfdp(1) – Linux man page
https://linux.die.net/man/1/sfdp - Plain-text diagrams take shape in Asciidoctor!
http://asciidoctor.org/news/2014/02/18/plain-text-diagrams-in-asciidoctor/ - Graphviz – Graph Visualization Software
http://www.graphviz.org/ - graphviz (Manual Page)
http://www.root.cz/man/7/graphviz/ - dot (Manual page)
http://www.root.cz/man/1/dot/ - dot (Manual v PDF)
https://graphviz.org/pdf/dot.1.pdf - Ditaa home page
http://ditaa.sourceforge.net/ - Ditaa introduction
http://ditaa.sourceforge.net/#intro - Ditaa usage
http://ditaa.sourceforge.net/#usage - Node, Edge and Graph Attributes
http://www.graphviz.org/doc/info/attrs.html - Graphviz (Wikipedia)
http://en.wikipedia.org/wiki/Graphviz - Unified Modeling Language
https://en.wikipedia.org/wiki/Unified_Modeling_Language - UML basics: The sequence diagram
http://www.ibm.com/developerworks/rational/library/3101.html - UML 2 State Machine Diagrams: An Agile Introduction
http://www.agilemodeling.com/artifacts/stateMachineDiagram.htm - Sequence diagram (Wikipedia)
https://en.wikipedia.org/wiki/Sequence_diagram - UML 2 Sequence Diagrams: An Agile Introduction
http://www.agilemodeling.com/artifacts/sequenceDiagram.htm - A Quick Introduction to UML Sequence Diagrams
http://www.tracemodeler.com/articles/a_quick_introduction_to_uml_sequence_diagrams/ - UML Sequence Diagrams
https://www.uml-diagrams.org/sequence-diagrams.html - Web Sequence Diagrams
https://www.websequencediagrams.com/ - Drawing sequence diagrams “napkin style”
https://modeling-languages.com/drawing-sequence-diagrams-napkin-style/ - Curated list of UML tools – 2020 edition
https://modeling-languages.com/uml-tools/#textual - Flowchart diagrams vs. UML activity diagrams
https://stackoverflow.com/questions/7081215/flowchart-diagrams-vs-uml-activity-diagrams - Kopenograms – Graphical Language for Structured Algorithms
https://kopenogram.org/Assets/Kopenograms_Graphical_Language_for_Structured_Algorithms.pdf - Kopenograms and Their Implementation in BlueJ
https://link.springer.com/chapter/10.1007%2F978–3–319–46535–7_8 - The simplest way to describe your flows
https://code2flow.com/ - Allan Mogensen and his Legacy
http://www.worksimp.com/articles/allan-mogensen.htm - Diagrams: Diagram as Code
https://diagrams.mingrammer.com/ - Diagrams: Guides
https://diagrams.mingrammer.com/docs/guides/diagram - Diagrams: Nodes
https://diagrams.mingrammer.com/docs/nodes/onprem - go-diagrams
https://github.com/blushft/go-diagrams - GoJS
https://gojs.net/latest/index.html - Code visualization: How to turn complex code into diagrams
https://www.lucidchart.com/blog/visualize-code-documentation - Create dependency diagrams from your code
https://docs.microsoft.com/en-us/visualstudio/modeling/create-layer-diagrams-from-your-code?view=vs-2019 - Software Architecture Diagrams as Code
https://shekhargulati.com/2020/04/21/software-architecture-diagrams-as-code/ - Processing spreadsheet data in Go
https://appliedgo.net/spreadsheet/ - Stránka projektu plotly
https://plot.ly/ - Plotly JavaScript Open Source Graphing Library
https://plot.ly/javascript/ - Domain coloring
https://en.wikipedia.org/wiki/Domain_coloring - The Gonum Numerical Computing Package
https://www.gonum.org/post/introtogonum/ - Gomacro na GitHubu
https://github.com/cosmos72/gomacro - gophernotes – Use Go in Jupyter notebooks and nteract
https://github.com/gopherdata/gophernotes - gonum
https://github.com/gonum - go-gota/gota – DataFrames and data wrangling in Go (Golang)
https://porter.io/github.com/go-gota/gota - A repository for plotting and visualizing data
https://github.com/gonum/plot - Gonum Numerical Packages
https://www.gonum.org/ - Getting started with Go modules
https://medium.com/@fonseka.live/getting-started-with-go-modules-b3dac652066d - Create projects independent of $GOPATH using Go Modules
https://medium.com/mindorks/create-projects-independent-of-gopath-using-go-modules-802260cdfb51o - Anatomy of Modules in Go
https://medium.com/rungo/anatomy-of-modules-in-go-c8274d215c16 - Modules
https://github.com/golang/go/wiki/Modules - Go Modules Tutorial
https://tutorialedge.net/golang/go-modules-tutorial/ - Module support
https://golang.org/cmd/go/#hdr-Module_support - Go vs. Python
https://www.peterbe.com/plog/govspy - PackageManagementTools
https://github.com/golang/go/wiki/PackageManagementTools - Sketchviz
https://sketchviz.com/ - SchemaSpy (verze pro starší JVM)
http://schemaspy.sourceforge.net/ - GitHub na GitHubu
https://github.com/schemaspy/schemaspy




































