Obsah
1. Reprezentace celočíselných hodnot v pracovních registrech i operační paměti
2. Celá čísla bez znaménka
3. Celá čísla se znaménkem (dvojkový doplněk)
4. ALU a základní matematické operace
5. Zvýšení či snížení hodnoty pracovního registru o 1
6. Aritmetické instrukce ADD (addition)
7. Aritmetická instrukce ADC (addition with carry)
8. Aritmetické instrukce SUB (subtraction) a SBB (subtraction with borrow)
9. Obsah další části tohoto seriálu
1. Reprezentace celočíselných hodnot v pracovních registrech i operační paměti
Aritmeticko-logická jednotka dokáže provádět aritmetické operace pouze s celočíselnými hodnotami, přičemž pro práci s jinými formami reprezentace číselných hodnot slouží matematické koprocesory či relativně samostatné jednotky určené pro operace s hodnotami uloženými ve formátu plovoucí řádové čárky (FPU). Většina současných mikroprocesorů při práci s celými čísly umožňuje provádění aritmetických operací s hodnotami reprezentovanými buď v systému dvojkového doplňku (signed integers) nebo s celými kladnými (bezznaménkovými) čísly (unsigned integers) – ve skutečnosti mezi těmito dvěma formami reprezentace mikroprocesor, resp. jeho ALU, nečiní velké rozdíly, což nás ovšem může v některých případech „vytrestat“ (problémové jsou například aritmetické posuvy, podmíněné skoky atd.). Vzhledem k tomu, že náš učební mikroprocesor je plně šestnáctibitový, tj. jeho pracovní registry i aritmeticko-logická jednotka dokážou v jedné instrukci pracovat se šestnáctibitovou hodnotou či dvěma hodnotami, existuje celkem 216=65536 navzájem různých stavů, které lze vhodnými i méně vhodnými způsoby mapovat na celá čísla (se znaménkem nebo bez znaménka).

Některé mikroprocesory a mikrořadiče jsou umístěny v pouzdrech s minimálním počtem vývodů
2. Celá čísla bez znaménka
Nejprve se podívejme, jak toto mapování vypadá v případě použití datového typu unsigned integer. Náš mikroprocesor (přesněji řečeno jeho aritmeticko-logická jednotka) používá takzvané přirozené mapování, ovšem ve speciálních případech se na některých mikroprocesorech volí mapování jiné. V minulosti byl například oblíbený Aikenův kód. Tabulka uvedená níže, která je platná pro přirozené mapování, nás pravděpodobně ničím nepřekvapí: pokud jsou všechny bity čísla vyjádřeného ve dvojkové soustavě nulové, jedná se skutečně o nulu; číselná řada postupně roste až k maximální hodnotě představované šestnácti bity nastavenými na I, což v dekadickém zápisu odpovídá 216-1=65535 (nesmíme totiž zapomenout na to, že jeden stav musí být vyhrazen pro nulu).
| Hexadecimální hodnota | Dekadický ekvivalent |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0002 | 2 |
| … | .. |
| 000f | 15 |
| 0010 | 16 |
| … | .. |
| 7ffd | 32765 |
| 7ffe | 32766 |
| 7fff | 32767 |
| 8000 | 32768 |
| 8001 | 32769 |
| 8002 | 32770 |
| … | .. |
| fffc | 65532 |
| fffd | 65533 |
| fffe | 65534 |
| ffff | 65535 |

Mikroprocesor s vývody určenými pro povrchovou montáž
3. Celá čísla se znaménkem (dvojkový doplněk)
Celá čísla se znaménkem jsou v moderních mikroprocesorech prakticky vždy reprezentována ve dvojkovém doplňku, neboť se jedná o reprezentaci umožňující použití stejné ALU pro práci s čísly se znaménkem i bez znaménka. Nejvyšší bit je v tomto případě vyhrazen pro znaménko, přičemž 0 značí, že se jedná o kladné číslo a I naopak označuje číslo záporné. Záporná čísla mají navíc invertovány všechny své bity (inverzí se vlastně automaticky nastaví znaménkový bit) a po inverzi je k nim přičtena jednička. Toto na první pohled nelogické uspořádání s sebou přináší řadu výhod, mezi jinými například tu, že existuje pouze jeden způsob zápisu nuly (nerozlišuje se kladná a záporná nula), při sčítání a odčítání může mikroprocesor použít stejné operace jako v případě bezznaménkových čísel atd., což si prakticky ukážeme v následujících částech tohoto seriálu. Převodní tabulka mezi interní reprezentací šestnáctibitové číselné hodnoty v počítači a jejím dekadickým ekvivalentem vypadá následovně:
| Hexadecimální hodnota | Dekadický ekvivalent | Poznámka |
|---|---|---|
| 0000 | 0 | nula je reprezentována jednoznačně |
| 0001 | 1 | |
| 0002 | 2 | |
| … | .. | |
| 000f | 15 | |
| 0010 | 16 | |
| … | .. | |
| 7ffd | 32765 | |
| 7ffe | 32766 | |
| 7fff | 32767 | nejvyšší kladné číslo |
| 8000 | –32768 | nejvyšší záporné číslo |
| 8001 | –32767 | |
| 8002 | –32766 | |
| … | .. | |
| fffc | –4 | |
| fffd | –3 | |
| fffe | –2 | |
| ffff | –1 | nejnižší záporné číslo |
Povšimněte si, že nejvyšší záporné číslo je v absolutní hodnotě o jedničku větší než nejvyšší kladné číslo. To je obecná vlastnost systému dvojkového doplňku a můžeme se s ní setkat na mnoha místech počítačového světa. Například i u některých vysokoúrovňových programovacích jazyků se při popisu jejich základních datových typů (primitivních typů) tato zákonitost objevuje.

David (Intel 4004)

A Goliáš (PA-RISC)
4. ALU a základní matematické operace
S pomocí aritmeticko-logické jednotky je možné – samozřejmě v závislosti na její konstrukci – provádět celou řadu aritmetických operací. Prakticky všechny mikroprocesory obsahují instrukci pro součet obsahu dvou registrů (mnemotechnická zkratka této instrukce je ADD), popř. součet obsahu dvou registrů s přičtením přenosu (mnemotechnická zkratka této instrukce je buď ADC nebo ADDC). Většina mikroprocesorů (s výjimkou například mikrořadičů řady 8048) obsahuje i instrukce pro rozdíl obsahu dvou registrů (SUB), popř. rozdíl s použitím přenosu z předchozí operace (SBC, nebo při opačném chápání přenosu SBB). Spolu se zvyšujícím se stupněm integrace a od ní odvozené možnosti použití více logických prvků se také rozšiřovaly aritmetické schopnosti ALU, což se projevilo například přidáním násobičky (obsahoval ji například slavný mikroprocesor Motorola 6809) a později dokonce i děličky.
Náš demonstrační mikroprocesor násobičku ani děličku neobsahuje, budeme se tedy muset spokojit se základními aritmetickými operacemi součtu a rozdílu. Jak si však ukážeme v následující části tohoto seriálu, je možné násobení a dělení naprogramovat pomocí instrukcí součtu a rozdílu doplněných o aritmetické posuvy o jeden bit doleva a doprava. Podívejme se tedy, které instrukce sloužív našem mikroprocesoru pro provádění základních aritmetických operací:
| Operační kód | Mnemotechnická zkratka | Popis instrukce |
|---|---|---|
| 00 | ADD | součet obsahu registrů A a B |
| 01 | ADC | součet obsahu registrů s přenosem |
| 02 | SUB | rozdíl obsahu registrů A a B |
| 03 | SBB | rozdíl obsahu registrů s výpůjčkou |
| 04 | INC | zvětšení obsahu registru A či B o 1 |
| 05 | DEC | snížení obsahu registru A či B o 1 |
5. Zvýšení či snížení hodnoty pracovního registru o 1
Nejjednodušší jsou poslední dvě uvedené instrukce, tj. INC (inkrementace) a DEC (dekrementace). Instrukce INC slouží ke zvýšení obsahu pracovního registru A či pracovního registru B o jedničku. V případě, že hodnota daného registru je po provedení této operace nulová, je nastaven příznak Zero flag, čehož se může využít například při tvorbě počítaných programových smyček (tato situace nastane ve chvíli, kdy obsah registru byl roven 0×ffff a po přičtení a zanedbání přetečení se jako výsledek inkrementace vrátila hodnota 0×0000). Podobný význam má instrukce DEC, která od pracovního registru A či B jedničku naopak odečte a opět v závislosti na tom, zda je obsah registru nulový, nastaví příznak Zero flag. Ani jedna z těchto dvou operací nepracuje s příznakem Carry flag a není to vlastně ani nutné.

Zvýšení hodnoty pracovního registru A o jedničku s nastavením Zero flagu (signály posílané z řadiče nejsou zakresleny)
Vzhledem k tomu, že se mikroprocesor musí rozhodnout, který registr bude inkrementován či dekrementován, je operační kód instrukce doplněn adresní částí, tj. dalším bytem, ve kterém je zapsána hodnota specifikující daný registr. Jsou použity stejné adresní kódy jako u minule popsaných instrukcí MOV, tj. 00 pro pracovní registr A a 01 pro pracovní registr B. Ve strojovém kódu tedy zápis instrukcí inkrementace a dekrementace vypadá následovně:
| Strojový kód | Zápis v assembleru | Význam |
|---|---|---|
| 04 00 | INC A | inkrementace registru A |
| 04 01 | INC B | inkrementace registru B |
| 05 00 | DEC A | dekrementace registru A |
| 05 01 | DEC B | dekrementace registru B |
Převažující způsob použití těchto instrukcí spočívá v tvorbě počítaných programových smyček a také ve zpracování informací uložených do polí či seznamů. S výhodou je možné při programování využít faktu, že tyto instrukce žádným způsobem neovlivňují příznak Carry flag, který tak může být použit pro jiné účely, například při násobení dvou hodnot pomocí bitových posuvů. Změna příznaku Zero flag je naopak důležitá, protože slouží k tvorbě smyček s využitím skokových instrukcí JZ a JNZ.

Zvýšení hodnoty pracovního registru B o jedničku s nastavením Zero flagu
6. Aritmetické instrukce ADD (addition) a ADC (addition with carry)
Další aritmetickou instrukcí je instrukce ADD, která slouží k součtu obsahu dvou pracovních registrů a uložení výsledku do jednoho z těchto registrů. Vzhledem k tomu, že výsledkem součtu dvou šestnáctibitových čísel může být hodnota, která přes tento rozsah přeteče (0×8001+0×8001 je větší než 0×ffff), je při sčítání modifikován i obsah příznaku Carry flag. Pokud je výsledek menší než 0×10000, je Carry flag nastaven na nulovou hodnotu, pokud dojde k přetečení přes 0×ffff, je Carry flag nastaven na logickou jedničku. Tato instrukce také v závislosti na výsledku součtu modifikuje příznak Zero flag: v případě, že výsledek je roven 0×0000 (popř. při přetečení 0×10000), je příznak Zero flag nastaven na jedničku, ve všech dalších případech je tento příznak nastaven na nulu. Vzhledem k tomu, že instrukce ADD vyžaduje dva operandy (sčítance) a výsledek se vrací do libovolného pracovního registru, existují celkem čtyři varianty této instrukce. Jednotlivé varianty jsou odlišeny adresním bytem, podobně jako u předchozích instrukcí:
| Strojový kód | Zápis v assembleru | Význam |
|---|---|---|
| 00 00 | ADD A,A | A←A+A |
| 00 01 | ADD A,B | A←A+B |
| 00 10 | ADD B,A | B←A+B |
| 00 11 | ADD B,B | B←B+B |

Součet pracovních registrů A a B s uložením výsledku do registru A a ovlivněním příznaků Carry flag a Zero flag
V tabulce uvedené výše můžeme vidět, že první operand instrukce ADD současně určuje i pracovní registr, do kterého se výsledek uloží. Tímto způsobem bývají zakódovány instrukce u většiny současných mikroprocesorů, neboť se tím zkracuje adresní část instrukce oproti případu, kdy by musely být uvedeny jak oba vstupní pracovní registry, tak i registr výstupní (u našeho mikroprocesoru to není patrné, protože má pouze dva pracovní registry, ovšem například RISC procesory jich mají 32, 64 či více).

Součet pracovního registru A se sebou samým s ovlivněním příznaků Carry flag a Zero flag
7. Aritmetická instrukce ADC (addition with carry)
Druhou „sčítací“ instrukcí je aritmetická instrukce ADC, která taktéž provádí součet dvou pracovních registrů, ovšem do součtu vstupuje i obsah příznaku Carry flag, tj. místo operace r=r1+r2 je prováděna operace r=r1+r2+CF. Tato instrukce se využívá například při implementaci víceslovní aritmetiky, tj. výpočtů, které by v našem případě překročily hranici 16 bitů. V praxi to znamená to, že součet dvou třicetidvoubitových hodnot je proveden dvojicí operací: první operací je ADD (spodních šestnáct bitů), druhou operací je ADC (horních šestnáct bitů), protože při součtu dolní poloviny 32bitového slova může dojít k přetečení, které se promítne do součtu horní poloviny slova. Víceslovní aritmetiku lze implementovat prakticky na libovolném mikroprocesoru, tj. například i „staré“ osmibitové mikroprocesory mohou pracovat s 64bitovými čísly – jedinou nevýhodou bude poměrně značné zpomalení všech výpočtů. I instrukce ADC obsahuje adresní část:
| Strojový kód | Zápis v assembleru | Význam |
|---|---|---|
| 01 00 | ADC A,A | A←A+A+CF |
| 01 01 | ADC A,B | A←A+B+CF |
| 01 10 | ADC B,A | B←A+B+CF |
| 01 11 | ADC B,B | B←B+B+CF |
Instrukce ADC může v některých případech nahradit podmíněný skok, například tehdy, pokud potřebujeme v závislosti na nějaké podmínce zvyšovat hodnotu pracovního registru. Zde se uplatní součet s registrem majícím hodnotu 0, přičemž podmínka je zakódována v příznaku Carry flag: provede se instrukce r=r+0+CF=r+CF.
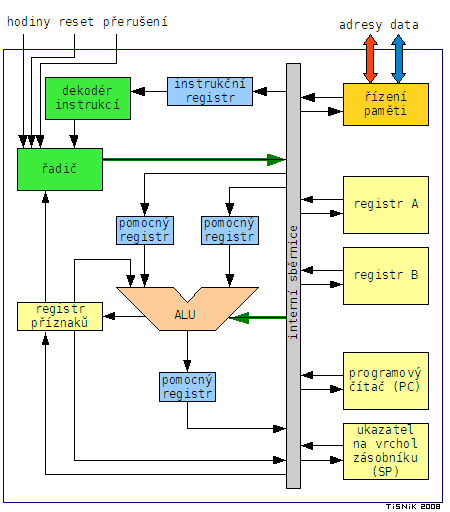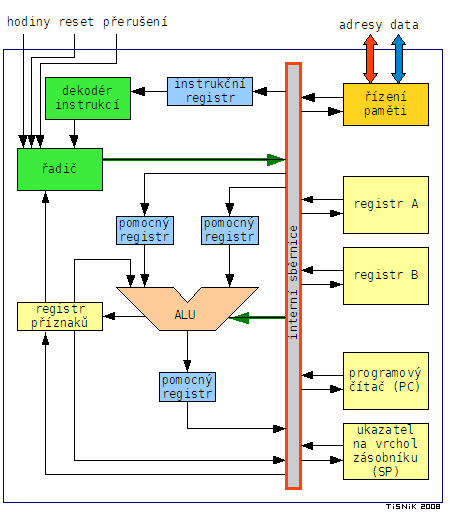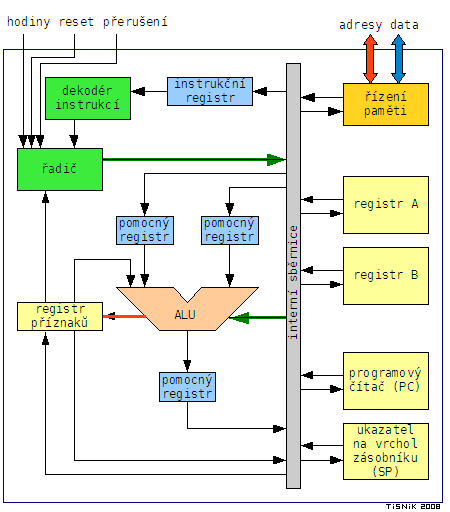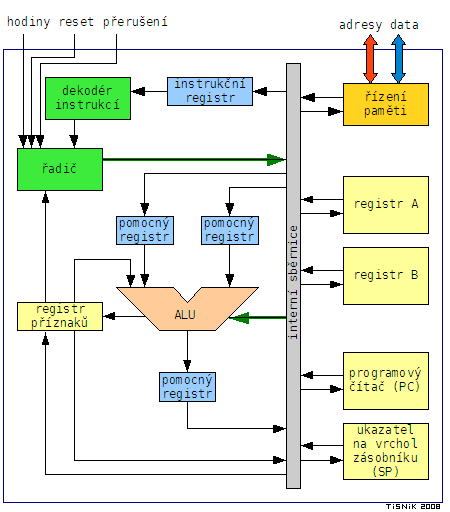
Součet pracovních registrů A a B s přičtením příznaku přetečení, s uložením výsledku do registru A a ovlivněním příznaků Carry flag a Zero flag
8. Aritmetické instrukce SUB (subtraction) SBB (subtraction with borrow)
Následuje aritmetická instrukce SUB, která představuje rozdíl hodnot dvou registrů. V závislosti na původním obsahu obou registrů, které vstupují do operace rozdílu je nastaven příznak Carry flag i Zero flag – první příznak je nastaven v případě, že došlo k přetečení přes nulu (0×10–0×20), druhý příznak v případě nulového výsledku (0×10–0×10), což vlastně znamená, že obsahy obou registrů, které do operace vstupovaly, jsou shodné. Ze zápisu všech kombinací této instrukce si všimněte, že zde záleží na pořadí operandů (na rozdíl od instrukce součtu) a také toho, že instrukce SUB A,A a SUB B,B vlastně provádí vynulování obsahu jednoho z pracovních registrů, což je důvod, proč náš mikroprocesor neobsahuje specializovanou instrukci, která by nulování pracovních registrů prováděla.
| Strojový kód | Zápis v assembleru | Význam |
|---|---|---|
| 02 00 | SUB A,A | A←A-A |
| 02 01 | SUB A,B | A←A-B |
| 02 10 | SUB B,A | B←B-A |
| 02 11 | SUB B,B | B←B-B |
Poslední aritmetickou instrukcí podporovanou naším mikroprocesorem je instrukce SBB. Tato instrukce také provádí výpočet rozdílu dvou pracovních registrů, navíc však od výsledku odečte obsah příznaku Carry flag (zde se s ohledem na význam tohoto příznaku místo slova „carry“, tj. přenos, častěji používá slovo „borrow“, tj. výpůjčka). Ve skutečnosti se tedy provádí operace r=r1-r2-CF. Je zapotřebí si dát pozor na to, že některé mikroprocesory (v minulosti například známý MOS 6502) obsahovaly instrukci SBC, která pracovala s negací Carry flagu, tj. prováděla se operace r=r1-r2-neg(CF) (u 6502 byla situace složitější v tom, že zde nebyla instrukce SUB, což znamenalo, že se běžné odečítání provádělo nastavením Carry flag do jedničky následovaným instrukcí SBC). I instrukce SBB existuje ve čtyřech variantách odlišených adresní částí:
| Strojový kód | Zápis v assembleru | Význam |
|---|---|---|
| 03 00 | SBB A,A | A←A-A-CF |
| 03 01 | SBB A,B | A←A-B-CF |
| 03 10 | SBB B,A | B←B-A-CF |
| 03 11 | SBB B,B | B←B-B-CF |

Rozdíl pracovních registrů A a B s odečtením příznaku přetečení, s uložením výsledku do registru B a ovlivněním příznaků Carry flag a Zero flag
9. Obsah další části tohoto seriálu
V další části seriálu, ve kterém se věnujeme funkcím počítače a především mikroprocesoru, si popíšeme všechny logické operace prováděné aritmeticko-logickou jednotkou (ALU). Také si ukážeme způsob použití operací pro bitové rotace a posuvy, například při násobení dvou čísel – tuto základní aritmetickou operaci totiž náš ukázkový mikroprocesor nepodporuje, podobně jako mnoho dalších mikroprocesorů a mikrořadičů.