Obsah
1. Nepřímý důsledek Moorova zákona – SIMD instrukce
2. Od klasické von Neumannovy architektury k paralelním výpočtům
3. Architektura x86–64 s nepřeberným množstvím skupin SIMD instrukcí
4. Instrukční sada MMX: první pokus o použití SIMD na platformě x86
5. Registry MMX, vztah ke standardnímu matematickému koprocesoru
6. SIMD instrukce v rozšiřující instrukční sadě 3DNow!
7. Registry používané v rozšíření 3DNow!
8. Nové SIMD instrukce v rozšíření 3DNow!
9. SIMD instrukce v rozšíření SSE
10. Sada registrů použitelná vývojáři pracujícími s procesory podporujícími SSE
11. Nové instrukce přidané v technologii SSE
12. Rozšíření instrukční sady SSE2
13. Nové instrukce přidané v rámci rozšíření instrukční sady SSE2
14. Seznam všech instrukcí SSE2
15. Podpora SIMD instrukcí v GCC – vektorová rozšíření
16. Základní aritmetické operace s vektory
18. Vektory s hodnotami s plovoucí řádovou čárkou
19. Repositář s demonstračními příklady
1. Nepřímý důsledek Moorova zákona – SIMD instrukce
„…sequential computers are approaching a fundamental physical limit on their potential power. Such a limit is the speed of light…“
V dnešním článku si ukážeme, jakým způsobem je možné v GCC (přesněji řečeno v překladači C, který patří do rodiny překladačů GCC) používat SIMD instrukce, které jsou zde souhrnně nazývány (i když ne zcela přesně) vektorové instrukce. Přitom SIMD/vektorové instrukce v současnosti patří ke standardní výbavě prakticky všech variant moderních mikroprocesorů. Připomeňme si, že z hlediska dosahovaného výpočetního výkonu leží na samém „výkonnostním dně“ klasické mikroprocesory s architekturou CISC, které vykonávají všechny instrukce postupně a dokončení jedné instrukce může v závislosti na jejich složitosti trvat i několik desítek strojových taktů. Předností těchto procesorů může být poměrně velká informační hustota instrukční sady (například i díky tomu, že operandy některých instrukcí jsou zadány implicitně), což mj. znamená, že se procesory tohoto typu po poměrně dlouhou dobu obešly bez nutnosti využití drahých vyrovnávacích pamětí první a druhé úrovně (L1 cache, L2 cache). Klasické procesory s architekturou CISC byly založeny na mikroprogramovém řadiči vybaveném pamětí mikroinstrukcí a teprve později začaly být tyto procesory doplňovány technologiemi získanými z jiných architektur – instrukční pipeline, prediktorem skoků, vektorovými instrukcemi (což byly oblasti klasických RISCových architektur) atd.

Obrázek 1: Ukázka časování instrukce ADC (Add with carry) dnes již klasického osmibitového mikroprocesoru MOS 6502 s architekturou CISC. V závislosti na zvoleném adresním režimu se liší počty strojových cyklů od dvou do šesti. Liší se samozřejmě i počet bajtů nutných pro zakódování instrukce, protože některé adresní režimy vyžadují zápis absolutní 16bitové adresy a jiné režimy používají jen 8bitový offset, popř. osmibitovou adresu v rámci takzvané nulté stránky (zero page).
Výpočetní výkon mikroprocesorů se podařilo poměrně výrazným způsobem zvýšit u architektury RISC zavedením instrukční pipeline. Provedení jedné instrukce sice stále trvalo větší počet strojových cyklů, ovšem díky rozfázování operací v instrukční pipeline bylo umožněno překrývání většího množství instrukcí, a to bez nutnosti zavádění skutečné paralelizace (která vede k velkému nárůstu složitosti a tím i ceny čipu). Spolu se zavedením mikroprocesorů RISC se skutečně stalo, že reálný i špičkový výpočetní výkon procesorů vzrostl, ale relativně brzy bylo nutné k těmto čipům přidat vyrovnávací paměti (cache), jelikož rychlost procesorů rostla mnohem rychleji, než vybavovací doba pamětí. Tento rozpor mezi rychlostmi obou nejdůležitějších součástí moderních počítačů ostatně trvá dodnes.
Pro další zvýšení výpočetního výkonu však bylo nutné použít další technologie, například instrukční sadu VLIW, která však – opět – měla velké nároky na rychlost pamětí. Podobně jako u procesorů RISC, i u VLIW bylo pro zmírnění požadavků na rychlost pamětí možné použít Harvardskou architekturu, tj. odděleni paměti programu od paměti dat (programová paměť navíc mohla mít větší šířku datové sběrnice odpovídající šířce instrukčních slov). Další zvýšení výkonu umožňují právě vektorové instrukce (SIMD), které ale mají jeden poměrně zásadní nedostatek – sémantickou mezeru mezi imperativním „skalárním“ kódem psaným například v C (C++ atd.) a instrukční sadou, která je SIMD (jinými slovy – běžné programovací jazyky neumožňují dostatečně popsat vektorové operace). Tuto mezeru do určité míry vyplňuje právě rozšíření GCC, kterému se budeme věnovat.
2. Od klasické von Neumannovy architektury k paralelním výpočtům
Všechny CISCové mikroprocesory firmy Intel řady 80×86, od ještě z poloviny osmibitového čipu Intel 8088 (právě ten byl použit v IBM PC, které tak není čistě 16bitovou architekturou), až po model Intel 80486 (včetně) byly založeny na skalární architektuře SISD, stejně jako velké množství dobových mikrořadičů či digitálních signálových procesorů (DSP – Digital Signal Processor). Nevýhodou systémů SISD ovšem je, že rychlost načítání a tím i zpracování instrukcí je shora omezena a že ani s využitím velmi dlouhé instrukční pipeline se nedá – vcelku logicky – překonat limit jedné zpracované instrukce za jeden takt. Příliš velké množství řezů (slices) pipeline má naopak i své zápory, především při zpracování skoků, návratů z podprogramů či odezvy na přerušení – ve všech těchto případech je nutné vyřešit problém, co se má udělat s instrukcemi, které se nachází v rozpracovaném stavu v pipeline (mohou se buď zahodit nebo naopak dokončit, podle toho, jakým způsobem byl lineární běh programu přerušen). To čipy komplikuje, vyžaduje kvalitní prediktory skoků, kvalitní překladače atd.

Obrázek 2: Schéma systému patřícího do kategorie SISD.
V současnosti se těší značné popularitě mikroprocesory patřící do kategorie SIMD, jejíž kořeny ovšem sahají hluboko do minulosti, konkrétně do šedesátých a sedmdesátých let minulého století (tato oblast výpočetní techniky je spojena se Symourem Crayem a jeho slavnými superpočítači – ty byly skutečně vektorové). Do této kategorie patří ty architektury procesorů, u kterých se s využitím jediné instrukce může zpracovat větší množství dat. Například u rozšířené instrukční sady MMX, s níž se seznámíme níže, je možné pomocí jediné instrukce provést součet dvou vektorů číselných hodnot. Může se jednat o osm osmibitových hodnot uložených v jednom vektoru, čtyři šestnáctibitové hodnoty v jednom vektoru atd. A u SSE/SSE2 jsou délky vektorů ještě násobně větší. Této vlastnosti se dá v mnoha případech využít pro urychlení běhu programů, protože některé algoritmy (ve skutečnosti je těchto algoritmů možná až udivující počet) provádí velké množství stejných operací s rozsáhlým objemem dat – například se může jednat o aplikaci konvolučního filtru na rastrový obrázek, zpracování zvukového signálu, vynásobení matice vektorem, vynásobení dvou matic atd.

Obrázek 3: Schéma systému patřícího do kategorie SIMD.
Mezi přednosti čipů náležejících do kategorie SIMD patří jak relativně kompaktní instrukční sada (což ovšem není případ x86 a x86–64!), tak i paralelní a tím pádem i rychlý běh mnoha algoritmů, ovšem za cenu větších nároků kladených na programátora, popř. na překladač. Stále jen poměrně velmi malé množství programovacích jazyků totiž umožňuje explicitně vyjádřit vektorové či maticové operace (například u překladače Fortranu určeného pro superpočítače Cray bylo v manuálu explicitně řečeno, které jazykové konstrukce se budou skutečně provádět ve vektorové – SIMD – jednotce). Z tohoto důvodu také není možné většinu SIMD konstrukcí zapsat v konvenčním vyšším programovacím jazyce: musí se použít buď hotová makra, ručně optimalizované knihovní funkce nebo specializované programovací jazyky (popř. de facto rozšíření typového systému, které si uvedeme v dnešním článku). Určitou, ale nezanedbatelnou výjimku představují GPU na grafických akcelerátorech, které explicitně pracují s 2D a 3D vektory, přičemž programátor může předem zjistit, které operace budou skutečně provedeny paralelně.

Obrázek 4: Typy vektorů, s nimiž pracují instrukce MMX.
3. Architektura x86–64 s nepřeberným množstvím skupin SIMD instrukcí
Jak jsme se již několikrát zmínili v předchozích odstavcích, jsou v soudobých typech mikroprocesorů implementovány i některé vektorové instrukce (popravdě řečeno již celkový počet vektorových instrukcí pravděpodobně překročil počet instrukcí skalárních, a to pravděpodobně několikanásobně :-). Pokud prozatím zůstaneme u platformy x86, tak historicky první instrukční sadou (přesněji řečeno doplněním původní instrukční sady) s podporou vektorových operací byla sada instrukcí MMX, s níž přišla firma Intel. Tato sada sice umožňovala provádění vektorových operací, ale měla celou řadu omezení, především nízký počet „vektorových“ registrů, které navíc měly (z dnešního pohledu) malou bitovou šířku a z toho vycházející nízký počet prvků umístitelných ve vektorech atd. Nevýhodné taktéž bylo, že se pro instrukce MMX používaly registry určené původně pro práci s matematickým koprocesorem (FPU), takže současné provádění FP operací a MMX operací bylo minimálně složité; většinou i zcela nepraktické. Ovšem poměrně brzy po uvedení sady MMX se objevila konkurenční instrukční sada 3Dnow! firmy AMD, která byla následovaná již zmíněnými sadami SSE až SSE5. Podrobnější informace o všech těchto instrukčních sadách si řekneme v navazujících kapitolách.

Obrázek 5: Dnes již historický mikroprocesor AMD K6–2 implementující mj. i rozšíření instrukční sady nazvané poněkud zvláštně 3Dnow!
Zkusme se nyní podívat na seznam různých SIMD (neboli nesprávně řečeno „vektorových“) rozšíření původní instrukční sady x86:
| Technologie | Rok uvedení | Společnost | Poprvé použito v čipu |
|---|---|---|---|
| MMX | 1996 | Intel | Intel Pentium P5 |
| 3DNow! | 1998 | AMD | AMD K6–2 |
| SSE | 1999 | Intel | Intel Pentium III (mikroarchitektura P6) |
| SSE2 | 2001 | Intel | Intel Pentium 4 (mikroarchitektura NetBurst) |
| SSE3 | 2004 | Intel | Intel Pentium 4 (Prescott) |
| SSSE3 | 2006 | Intel | mikroarchitektura Intel Core |
| SSE4 | 2006 | Intel+AMD | AMD K10 (SSE4a) , mikroarchitektura Intel Core |
| SSE5 | 2007 | AMD | (nakonec rozděleno do menších celků), mikroarchitektura Bulldozer |
| AVX | 2008 | Intel | mikroarchitektura Sandy Bridge |
| F16C (CVT16) | 2009 | AMD | Jaguar, Puma, Bulldozer atd. |
| XOP | 2009 | AMD | mikroarchitektura Bulldozer |
| FMA3 | 2012 | AMD | mikroarchitektura Piledriver, Intel: Haswell a Broadwell |
| FMA4 | 2011 | AMD | mikroarchitektura Bulldozer (pozdější architektury po Zen 1 již ne) |
| AVX2 | 2013 | Intel | mikroarchitektura Haswell |
| AVX-512 | 2013 | Intel | Knights Landing |
| AMX | 2020 | Intel | Sapphire Rapids |
To, jaká rozšíření instrukční sady podporuje váš mikroprocesor, lze získat snadno:
$ cat /proc/cpuinfo
V mém konkrétním případě (Intel® Core™ i7–8665U CPU @ 1.90GHz) se vypíšou následující vlastnosti CPU. Z těchto příznaků jsem zdůraznil příznaky odpovídající SIMD instrukcím:
flags : fpu vme de pse tsc msr pae mce cx8 apic sep mtrr pge mca cmov pat pse36 clflush dts acpi mmx fxsr sse sse2 ss ht tm pbe syscall nx pdpe1gb rdtscp lm constant_tsc art arch_perfmon pebs bts rep_good nopl xtopology nonstop_tsc cpuid aperfmperf pni pclmulqdq dtes64 monitor ds_cpl vmx smx est tm2 ssse3 sdbg fma cx16 xtpr pdcm pcid sse4_1 sse4_2 x2apic movbe popcnt tsc_deadline_timer aes xsave avx f16c rdrand lahf_lm abm 3dnowprefetch cpuid_fault epb invpcid_single ssbd ibrs ibpb stibp ibrs_enhanced tpr_shadow vnmi flexpriority ept vpid ept_ad fsgsbase tsc_adjust bmi1 avx2 smep bmi2 erms invpcid mpx rdseed adx smap clflushopt intel_pt xsaveopt xsavec xgetbv1 xsaves dtherm ida arat pln pts hwp hwp_notify hwp_act_window hwp_epp md_clear flush_l1d arch_capabilities
Pro někoho může být taktéž zajímavá i informace o tom, jak velké změny v instrukční sadě mikroprocesorů byly vlastně při přidávání nových „vektorových“ rozšiřujících instrukčních sad typu SIMD provedeny. To nám ukáže další tabulka. Je pouze nutné dát si pozor na to, že počty nových instrukcí zavedených v rámci těchto nových technologií, které jsou vypsány v tabulce pod odstavcem, nemusí přesně souhlasit s počty uváděnými v jiných informačních materiálech. Je tomu tak především z toho důvodu, že se v některých případech rozlišuje i datový typ, s nímž instrukce pracují (například se může jednat o součet vektoru s 32 bitovými hodnotami nebo 64bitovými hodnotami reprezentovanými v obou případech ve formátu s plovoucí řádovou čárkou) a někdy se taková instrukce do celkové sumy započítává pouze jedenkrát. Nicméně údaje vypsané v níže uvedené tabulce by měly být konzistentní, protože se jedná o počty nově přidaných operačních kódů instrukcí (například u dále popsané instrukční sady SSE2 končí instrukce znakem D, S, I či Q podle typu zpracovávaných dat/operandů):
| Název technologie | Počet nových instrukcí |
|---|---|
| MMX | 56 |
| 3DNow! | 21 |
| SSE | 70 |
| SSE2 | 144 |
| SSE3 | 13 |
| SSSE3 | 32 (ve skutečnosti vlastně jen 16 instrukcí, ovšem pro dva datové typy) |
| SSE4 | 54 (z toho 47 v rámci SSE4.1, zbytek v rámci SSE4.2) |
| SSE5 | 170 (z toho 46 základních instrukcí) |
| F16C | 4 |
4. Instrukční sada MMX: první pokus o použití SIMD na platformě x86
První rozšiřující instrukční sadou navrženou pro procesory na platformě x86 (tedy nikoli ještě x86–64), která obsahovala SIMD operace, je sada instrukcí nazvaná MMX (MultiMedia eXtension, později taktéž rozepisováno jako Matrix Math eXtension). Tato sada byla navržena již v roce 1996 ve společnosti Intel a od roku 1997 jí začaly být vybavovány prakticky všechny nové mikroprocesory této firmy, přesněji řečeno ty mikroprocesory, které patřily do rodiny x86 (připomeňme si, že se jednalo o 32bitové mikroprocesory, protože k rozšíření na 64bitovou ALU došlo u mainstreamových čipů až o několik let později). Prvním mikroprocesorem s plnou podporou MMX byl čip Pentium P55C nabízený od začátku roku 1997. Později došlo k implementaci instrukční sady MMX i na čipy Pentium II a procesory konkurenčních společností, konkrétně na čipy AMD K6 a taktéž na Cyrix M2 (6×86MX) a IDT C6.
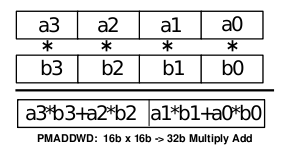
Obrázek 6: Jedna z poměrně složitých, ale užitečných instrukcí z instrukční sady MMX. Jedná se konkrétně o instrukci PMADDWD, která provádí paralelní součin čtveřice šestnáctibitových hodnot s 32 bitovým mezivýsledkem, s následným součtem prvního + druhého a třetího + čtvrtého mezivýsledku. Tuto instrukci lze použít například při implementaci konvolučních filtrů.
(Zdroj: Intel MMXTM Technology Overview, Intel corporation, 1996)
Jedním z důvodů zavedení těchto nových instrukcí byla snaha společnosti Intel o konstrukci osobních počítačů s minimálním množstvím specializovaných čipů na základní desce i na přídavných kartách. Většinu operací měl totiž (podle tehdejších představ) provádět samotný mikroprocesor, ať již se jednalo o zpracování zvuku (softwarový mix), ovládání periferních zařízení (programová implementace bufferů atd.) tak i o softwarovou implementaci kodeků, včetně kodeků používaných v modemech (právě v té době došlo k rozvoji takzvaných softwarových modemů, jejichž příslušenství se zúžilo na pouhé elektrické rozhraní pro analogovou telefonní linku). V rámci instrukční sady MMX se na původně prakticky ryze skalární platformu x86 přidalo celkem 57 nových instrukcí a čtyři datové typy, které byly těmito instrukcemi podporovány. Jeden z nově zaváděných datových typů je skalární, další tři nové datové typy jsou představovány dvouprvkovým, čtyřprvkovým a osmiprvkovým vektorem.
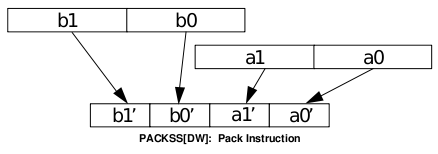
Obrázek 7: Ukázka jednoho typu konverzní funkce, kterých se v instrukční sadě MMX nachází několik.
(Zdroj: Intel MMXTM Technology Overview, Intel corporation, 1996)
Většina nových instrukcí přidaných v rámci sady MMX byla určena pro provádění aritmetických a bitových operací s celočíselnými operandy o šířce 8, 16, 32 či 64 bitů, což pokrývá poměrně širokou oblast multimediálních dat – osmibitových i šestnáctibitových zvukových vzorků (samplů), barev pixelů (RGB, RGBA) atd. Zatímco při provádění aritmetických operací s využitím klasické aritmeticko-logické jednotky mohlo docházet k přetečení či podtečení hodnot při provádění instrukcí typu ADD či SUB (součet, rozdíl), je možné u MMX instrukcí zvolit i takzvanou aritmetiku se saturací, což znamená, že v případě přetečení se do výsledku uloží maximální reprezentovatelná hodnota a naopak při podtečení minimální hodnota, což je například při zpracování signálu (většinou) žádoucí chování, V následující tabulce jsou vypsány nově podporované datové typy i způsob jejich uložení ve slovech o šířce 64 bitů, které jsou zpracovávány jednotkou MMX:
| Datový typ | Bitová šířka operandu | Počet prvků vektoru |
|---|---|---|
| packed byte | 8 bitů | 8 |
| packed word | 16 bitů | 4 |
| packed doubleword | 32 bitů | 2 |
| quadword | 64 bitů | 1 |
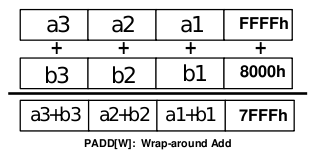
Obrázek 8: Ukázka chování MMX instrukce nazvané PADDW, která provádí součet čtveřice šestnáctibitových hodnot s přetečením, což je patrné z posledního sloupce.
(Zdroj: Intel MMXTM Technology Overview, Intel corporation, 1996)
Kromě přímé manipulace s celočíselnými hodnotami bylo relativně snadné pracovat i s numerickými hodnotami ukládanými ve formátu s pevnou řádovou čárkou (FX – fixed point), mohlo se například jednat o formáty 8.8 (osm bitů pro uložení celé části a osm bitů za řádovou čárkou), 8.24, 24.8 atd. O případné bitové posuny při normalizaci numerických hodnot se v tomto případě ovšem musel postarat programátor. Tyto formáty byly a jsou využívány v některých algoritmech implementujících FFT (rychlou Fourierovu transformaci využívanou v mnoha algoritmech pro zpracování signálů), DCT (diskrétní kosinovou transformaci využívanou například ve formátu JFIF-JPEG), FIR, IIR (filtry s konečnou a nekonečnou impulsní odezvou), operacemi nad vektory či operacemi nad maticemi.
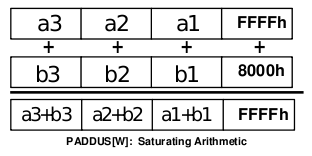
Obrázek 9: MMX instrukce nazvaná PADDUSW, která sice také provádí součet čtveřice šestnáctibitových hodnot, ovšem součet je proveden se saturací – v případě, že se výsledek součtu již nemůže reprezentovat šestnáctibitovou hodnotou, uloží se namísto výsledku hodnota 0×FFFF, tj. nejvyšší šestnáctibitové celé číslo bez znaménka.
(Zdroj: Intel MMXTM Technology Overview, Intel corporation, 1996)
Všech 57 instrukcí zavedených v instrukční sadě MMX lze rozdělit podle jejich funkce do několika skupin vypsaných v následující tabulce:
| # | Skupina instrukcí | Příklady instrukcí |
|---|---|---|
| 1 | Základní aritmetické operace | PADD, PADDS, PADDUS, PSUBS, PSUBUS, PMULHW, PMULLW |
| 2 | Logické (bitové) operace | PAND, PANDN, POR, PXOR |
| 3 | Bitové posuny | PSLL, PSRL, PSRA |
| 4 | Porovnávání | PCMPEQ, PCMGT |
| 5 | Konverze dat | PACKUSWB, PACKSS, PUNPCKH, PUNPCKL |
| 6 | Přenosy dat + práce s pamětí | MOV |
| 7 | Řízení jednotky MMX | EMMS |

Obrázek 10: Zdrojový rastrový obrázek (známá fotografie Lenny), který tvoří zdroj pro jednoduchý konvoluční (FIR) filtr, jenž zvyšuje hodnoty pixelů o pevně zadanou konstantu (offset).
Většina instrukcí uvedených v předchozí tabulce má navíc několik variant v závislosti na tom, s jakými operandy má instrukce ve skutečnosti pracovat. Například u instrukce PADD (tedy operace součtu) je možné zvolit, zda se mají sečíst dva osmiprvkové vektory, kde každý prvek má šířku 8 bitů, zda se má provést součet dvou čtyřprvkových vektorů (16bitové prvky), dvou dvouprvkových vektorů (32bitové prvky) či zda se jedná o součet dvojice 64bitových skalárních hodnot. To tedy znamená, že instrukce PADD může být reprezentována čtveřicí různých operačních kódů:
| # | Instrukce | Význam |
|---|---|---|
| 1 | PADDB | součet dvou vektorů majících osm osmibitových prvků |
| 2 | PADDW | součet dvou vektorů majících čtyři šestnáctibitové prvky |
| 3 | PADDD | součet dvou vektorů majících dva 32bitové prvky |
| 4 | PADDQ | součet dvou 64bitových skalárních hodnot |
Výjimkou z výše uvedeného pravidla jsou instrukce nazvané PAND, PANDN, POR a PXOR, pomocí nichž lze provádět bitové operace s dvojicí 64bitových slov. Důvod, proč není zapotřebí tyto instrukce dále rozdělovat podle počtu a šířky prvků vektorů, je zřejmý – tyto operace pracují nad jednotlivými bity, nikoli nad skupinami bitů. Na tomto místě je možná dobré upozornit na instrukci PANDN (not-and), která sice není ve většině běžných (skalárních) aritmeticko-logických jednotkách implementována, ovšem v případě zpracování rastrových obrazů se jedná o velmi užitečnou instrukci používanou například při vykreslování spritů atd.

Obrázek 11: Pokud je pro přičtení offsetu použita operace součtu se zanedbáním přenosu (carry), tj. když se počítá systémem „modulo N“ (viz též výše zmíněná instrukce PADDB), dochází při překročení maximální hodnoty pixelu (čistě bílá barva) k viditelným chybám.
5. Registry MMX, vztah ke standardnímu matematickému koprocesoru
Inženýři ve firmě Intel stáli při návrhu instrukční sady MMX před požadavkem na vytvoření výkonných instrukcí provádějících SIMD operace, na druhou stranu však bylo nutné šetřit počtem tranzistorů a tím pádem i plochou čipu, na němž byl mikroprocesor vytvořen. Navíc bylo nutné zachovat kompatibilitu s existujícími programy a operačními systémy, zejména při ukládání registrů na zásobník v subrutinách atd. Pravděpodobně právě z tohoto důvodu se rozhodli učinit poněkud problematický krok – navrhli MMX instrukce takovým způsobem, aby mohly pracovat s osmicí 64bitových registrů rozdělených na jeden, dva, čtyři či osm prvků. Ovšem nejednalo se, jak by se dalo předpokládat, o nové registry rozšiřující původní sadu registrů procesoru Pentium, ale o část registrů využívaných matematickým koprocesorem (FPU). Ten na platformě x86 prováděl operace s osmicí 80bitových registrů uspořádaných do zásobníku (u matematického koprocesoru Intel 8087 byly používány čistě zásobníkové instrukce, později byly přidány i další adresovací režimy, které umožňovaly registry adresovat přímo, což se ukázalo být výhodnější především kvůli možnostem provádění různých optimalizací).

Obrázek 12: Při použití operace součtu se saturací sice taktéž dojde ke ztrátě informace (vzniknou oblasti s pixely majícími hodnotu 255), ovšem viditelná chyba je mnohem menší, než na předchozím obrázku, kde docházelo k přetečení. Tento filtr by bylo možné realizovat s využitím instrukce PADDUSB s rychlostí výpočtu 8 pixelů/instrukci při bitové hloubce 8bpp.
V případě instrukcí MMX se sice registry adresovaly přímo (popř. se adresovala slova uložená v operační paměti, která mohla tvořit jeden z operandů instrukce), ale kvůli tomu, že jak FPU, tak i jednotka MMX pracovala se shodnými registry (horních 16 bitů těchto registrů nebylo v MMX využito), bylo současné používání SIMD operací a operací s hodnotami uloženými v systému plovoucí řádové čárky poměrně komplikované, což je škoda, protože právě souběžná práce superskalárního CPU (u mikroprocesorů Pentium byly vytvořeny dvě instrukční pipeline „u“ a „v“), jednotky MMX a navíc ještě matematického koprocesoru by v mnoha případech mohla vést k citelnému nárůstu výpočetního výkonu. V následující tabulce jsou vypsána jména registrů tak, jak jsou použita v instrukcích matematického koprocesoru, i ve formě používané jednotkou MMX::
| Registr FPU | bity 79–64 | bity 63–0 |
|---|---|---|
| ST0 | nepoužito | MM0 |
| ST1 | nepoužito | MM1 |
| ST2 | nepoužito | MM2 |
| ST3 | nepoužito | MM3 |
| ST4 | nepoužito | MM4 |
| ST5 | nepoužito | MM5 |
| ST6 | nepoužito | MM6 |
| ST7 | nepoužito | MM7 |

Obrázek 13: Typy vektorů, s nimiž pracují instrukce MMX.
6. SIMD instrukce v rozšiřující instrukční sadě 3DNow!
Rozšíření instrukční sady mikroprocesorů z rodiny x86 o instrukce MMX popsané v předchozích kapitolách bylo poměrně razantní – jednalo se v podstatě o největší změnu této architektury od vzniku procesoru 80386, tj. od zavedení virtuálního režimu, 32bitových pracovních registrů a pochopitelně i operací s 32 bitovými hodnotami. Z hlediska společnosti Intel se samozřejmě jednalo o nemalou konkurenční výhodu získanou nad firmami AMD, Cyrix či IDT (tedy tehdejšími konkurenty v segmentu), zejména poté, co se podpora MMX operací zařadila do některých programových produktů (například do zásuvných modulů Photoshopu, kde měla velký vliv). Ovšem tehdejší druhý největší výrobce čipů řady x86 – společnost AMD – o necelé dva roky později představila vlastní rozšíření instrukční sady, které bylo označeno poměrně nabubřelým názvem 3DNow! (a to včetně onoho vykřičníku na konci). Toto rozšíření instrukční sady bylo poprvé implementováno v mikroprocesoru AMD K6–2 a později též v čipu AMD K6–3 a Athlon.

Obrázek 14: Mikroprocesor AMD K6–2 implementující mj. i instrukční sadu 3DNow!
Inženýři ze společnosti AMD použili a současně i rozšířili instrukční sadu MMX o několik nových celočíselných instrukcí, ovšem hlavní konkurenční výhodou (a to poměrně podstatnou) byly nové instrukce pro práci s čísly reprezentovanými 32bitovými hodnotami s plovoucí řádovou čárkou (floating point). Kromě toho bylo do instrukční sady 3DNow! přidáno několik operací sloužících pro přečtení bloku dat do vyrovnávací paměti (cache). U některých typů mikroprocesorů (Athlon) bylo navíc možné určit, zda je blok dat načtených do vyrovnávací paměti určený pro čtení nebo i pro zápis (pokud se jednalo o blok určený pro zápis, byl mu nastaven atribut modified). To ovšem již vyžadovalo poměrně razantní zásahy do překladačů.

Obrázek 15: Další pohled na mikroprocesor AMD K6–2 s implementací instrukční sady 3DNow!.
7. Registry používané v rozšíření 3DNow!
Již v předchozí kapitole jsme se zmínili o tom, že instrukční sada 3DNow! byla vlastně rozšířením konkurenční instrukční sady MMX. To mj. znamená, že v 3DNow! byly podporovány všechny datové typy MMX, tj. konkrétně osmiprvkové vektory s osmibitovými hodnotami, čtyřprvkové vektory s 16bitovými hodnotami, dvouprvkové vektory s 32bitovými hodnotami a konečně i 64bitové skalární hodnoty. Navíc však bylo možné do 64bitových registrů MMX uložit dvojici 32bitových čísel s plovoucí řádovou čárkou odpovídající formátu single precision definovaném v normě IEEE 754. Zavedení tohoto nového typu dvouprvkového vektoru s sebou přinášelo dvě výhody: mnohé FP operace se mohly provádět paralelně (součet prvků vektorů atd.) a navíc bylo velmi snadné kombinovat původní celočíselné MMX operace s operacemi nad reálnými čísly. To nebylo u původní implementace MMX snadné, protože se muselo provádět přepínání mezi činností matematického koprocesoru a jednotkou MMX, jak jsme si již ostatně řekli v předchozím textu.
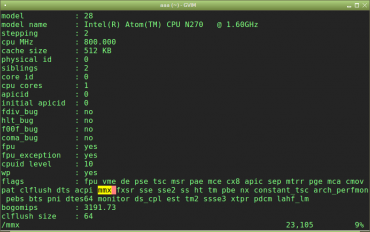
Obrázek 16: Mikroprocesor Intel Atom sice implementuje instrukční sadu MMX, ale nikoli 3Dnow!, což je ovšem více než kompenzováno podporou SSE a SSE2.
V případě instrukční sady 3DNow! se toto přepínání provádět nemuselo (pokud tedy nebylo nutné pracovat s hodnotami s dvojitou či rozšířenou přesností, tj. s datovými typy double a extended), navíc měli programátoři k dispozici konverzní instrukce nazvané PI2FD a PF2ID a určené pro převod celočíselných 32bitových hodnot na hodnoty s plovoucí řádovou čárkou (se zaokrouhlením) a naopak. Mimochodem: pro přepnutí kontextu mezi FPU operacemi a MMX/3DNow! operacemi bylo možné použít instrukci FEMMS určenou pro rychlé přepnutí kontextu. Tato operace je rychlejší, než původní instrukce EMMS ze sady MMX, ovšem po přepnutí je obsah pracovních registrů nedefinovaný (což v naprosté většině případů vůbec nevadí).
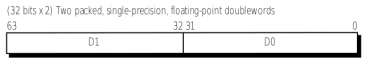
Obrázek 17: Uložení dvou 32bitových čísel s plovoucí řádovou čárkou v 64bitovém registru.
(Zdroj: 3Dnow! Technology Manual, AMD Inc.)
8. Nové SIMD instrukce v rozšíření 3DNow!
Všechny vektorové instrukce provádějící operace s 32bitovými numerickými hodnotami s plovoucí řádovou čárkou, které jsou implementovány v rámci instrukční sady 3DNow!, jsou pro větší přehlednost vypsány v následující tabulce:
| # | Instrukce | Popis |
|---|---|---|
| 1 | PI2FD | převod 32bitových celočíselných hodnot na FP hodnoty |
| 2 | PF2ID | převod 32bitových FP hodnot na celočíselné hodnoty |
| 3 | PFCMPGE | porovnání na relaci „větší nebo rovno“ |
| 4 | PFCMPGT | porovnání na relaci „větší než“ |
| 5 | PFCMPEQ | porovnání na relaci „rovnost“ |
| 6 | PFACC | součet obou prvků zdrojového registru i obou prvků cílového registru |
| 7 | PFADD | součet dvou dvouprvkových vektorů |
| 8 | PFSUB | rozdíl dvou dvouprvkových vektorů |
| 9 | PFSUBR | rozdíl dvou dvouprvkových vektorů s prohozením operandů |
| 10 | PFMIN | výpočet minima (vždy mezi příslušnými prvky vektorů) |
| 11 | PFMAX | výpočet maxima (vždy mezi příslušnými prvky vektorů) |
| 12 | PFMUL | součin dvou dvouprvkových vektorů |
| 13 | PFRCP | výpočet aproximace převrácené hodnoty |
| 14 | PFRSQRT | výpočet aproximace druhé odmocniny |
| 15 | PFRCPIT1 | první krok přesného výpočtu převrácené hodnoty |
| 16 | PFRSQIT1 | první krok přesného výpočtu druhé odmocniny |
| 17 | PFRCPIT2 | další krok výpočtu převrácené hodnoty či druhé odmocniny |
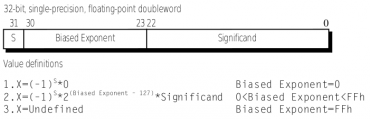
Obrázek 18: Formát 32bitových čísel s plovoucí řádovou čárkou podporovaný instrukcemi 3Dnow!)
(Zdroj: 3Dnow! Technology Manual, AMD Inc.)
Při provádění porovnání prvků dvou vektorů, tj. při provádění instrukcí pojmenovaných PFCMPGE, PFCMPGT a PFCMPEQ, je výsledkem této operace nový dvouprvkový vektor obsahující pouze hodnoty 0×0000_0000 a 0×FFFF_FFFF. U porovnávání se navíc nerozlišuje kladná a záporná nula, což je pro naprostou většinu výpočtů zcela korektní.
Pravděpodobně nejzajímavější je poslední pětice instrukcí nazvaných PFRCP, PFRSQRT, PFRCPIT1, PFRSQIT1 a PFRCPIT2. Instrukce PFRCP slouží k rychlému výpočtu převrácené hodnoty, ovšem pouze s přesností na 14 bitů. V případě, že tato přesnost není dostatečná (pro mnoho účelů, například grafiku, však stačí), musí být použita následující sekvence:
PFRCP ; první přiblížení k výsledku s přesností 14 bitů PFCPIT1 ; první krok přesného výpočtu převrácené hodnoty PFRCPIT2 ; druhý krok přesného výpočtu převrácené hodnoty
Důležité přitom je, že první přiblížení se k výsledku je provedeno velmi rychle, konkrétně pouze ve dvou taktech, protože se využívá tabulky výsledků umístěné v paměti ROM. Teprve další dvojice instrukcí využívá pomalejší iterační výpočet. Podobný princip platí i pro rychlý vs. přesný výpočet druhé odmocniny (opět lze využít například v grafice).

Obrázek 19: Subrutina pro operaci dělení s 24 bitovou přesností implementovanou pomocí instrukcí 3Dnow!.
(Zdroj: 3Dnow! Technology Manual, AMD Inc.)
9. SIMD instrukce v rozšíření SSE
Po úspěšném a relativně bezproblémovém zavedení rozšíření MMX i 3DNow! do praxe není divu, že obě nejvýznamnější společnosti podnikající v oblasti návrhu a prodeje mikroprocesorů patřících do rodiny x86, tj. tehdy už prakticky jen dvojice firem Intel a AMD, začaly pro tyto typy mikroprocesorů navrhovat i další rozšiřující instrukční sady s „vektorovými“ instrukcemi typu SIMD. Některé z dále zmíněných technologií byly použity v mikroprocesorech vyráběných jednou společností (což je především případ 3DNow!), ovšem v současnosti můžeme vidět oboustranné snahy o zavádění rozšíření instrukční sady x86 podle jednotného schématu a navíc tak, aby ho bylo možné používat na mikroprocesorech vyráběných oběma zmíněnými společnostmi. To je poměrně velký rozdíl oproti ad-hoc řešením, s nimiž jsme se setkali v případě MMX i 3DNow! (kde navíc byli výrobci čipů svázaní snahou o zachování zpětné kompatibility s existujícími operačními systémy).
Pro programátory je důležitá především dnes již zcela zavedená a široce podporovaná technologie SSE, což je zkratka znamenající Streaming SIMD Extension. Na SSE se můžeme dívat buď jako na zcela nové rozšíření instrukční sady o SIMD instrukce, nebo jako na určité propojení předností obou předchozích technologií, tj. jak MMX (relativně velký počet prvků uložených ve vektorech, ovšem podpora pouze pro celočíselné operace nad prvky vektorů), tak i 3DNow! (práce s reálnými čísly, ovšem uloženými pouze v dvouprvkových vektorech, z čehož vyplývají menší možnosti paralelizace výpočtů). V případě SSE je navíc umožněna souběžná práce jednotky MMX či FPU. Ve specifikaci SSE jsou popsány jak významy všech nových instrukcí, tak i různé režimy využívané při aritmetických operacích. Specifikace taktéž říká, jaké pracovní registry se u nových instrukcí používají.
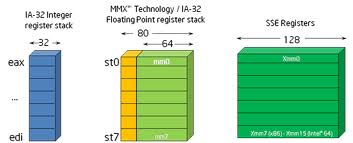
Nejprve se zaměřme na registry využívané v technologii SSE. U mikroprocesorů implementujících instrukční sadu SSE je využita nová sada registrů pojmenovaných XMM0 až XMM7. Na 64bitové platformě (původně architektura AMD 64, dnes pochopitelně podporováno i Intelem) navíc došlo k přidání dalších osmi registrů se jmény XMM8 až XMM15 využitelných pouze v 64bitovém režimu. Všechny nové registry mají šířku 128 bitů, tj. jsou dvakrát širší, než registry používané v MMX i 3DNow! a čtyřikrát širší, než běžné pracovní registry na platformě x86 (bavíme se o dnes již překonaném 32bitovém režimu). Do každého registru je možné uložit čtveřici reálných numerických hodnot reprezentovaných v systému plovoucí řádové tečky podle normy IEEE 754, přičemž tato norma je dodržována přesněji, než v případě 3DNow! (různé zaokrouhlovací režimy či práce s denormalizovanými čísly sice mohou vypadat trošku jako černá magie, ovšem například v knihovnách pro numerické výpočty, které musí vždy za specifikovaných okolností dát stejný výsledek, se jedná o velmi důležitou vlastnost). K osmi či šestnácti novým registrům XMM* byl ještě přidán jeden 32bitový registr nazvaný MXCSR, jenž byl určený pro nastavení (řízení) režimů výpočtu.
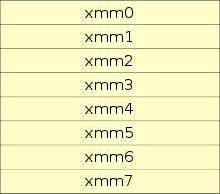
Obrázek 20: Sada nových pracovních registrů přidaných v rámci rozšíření instrukční sady SSE.
10. Sada registrů použitelná vývojáři pracujícími s procesory podporujícími SSE
Díky zavedení rozšíření instrukční sady SSE do praxe začali mít programátoři vytvářející aplikace na tehdy 32bitové platformě x86, jejíž začátek se datuje od dnes již spíše historického mikroprocesoru Intel 80386, k dispozici nejenom 64bitové registry (jednotka MMX), ale nyní už dokonce i registry 128bitové, což je zajisté užitečné. Přitom i přes zavedení rozšířených instrukčních sad MMX/3DNow!/SSE stále zůstávala zachována binární zpětná i dopředná kompatibilita s předchozími typy mikroprocesorů (nejedná se tedy o takovou změnu, jako v případě přechodu 16->32->64 bitů, která se týkala celé ALU). Zde je myšlena především možnost běhu starších aplikací na novějších mikroprocesorech, protože program přeložený s podporou SSE nebude na procesoru bez této technologie pracovat korektně, i když by pravděpodobně bylo možné SSE emulovat s využitím podprogramů spouštěných při zavolání neplatného operačního kódu (tj. operačního kódu SSE instrukce, která je samozřejmě pro ne-SSE procesor neznámým kódem).
Pro zajímavost se nyní podívejme, jak se společně se zavedením instrukční sady SSE prakticky zdvojnásobila celková kapacita všech využitelných pracovních registrů na 32bitové platformě x86 (na 64bitové x86_64 je situace odlišná, SSE je dnes její nedílnou součástí). V následující tabulce jsou kromě univerzálních pracovních registrů, indexových registrů a bázových registrů vypsány i registry se speciálním významem:
| # | Typ registrů | Počet registrů | Bitová šířka registru | Příklady |
|---|---|---|---|---|
| 1 | Univerzální registry | 4 | 32 bitů | EAX, EBX, ECX, EDX |
| 2 | Indexové registry | 3 | 32 bitů | ESI, EDI, EIP |
| 3 | Bázové registry | 2 | 32 bitů | EBP, ESP |
| 4 | Segmentové registry | 6 | 16 bitů | CS, DS, ES, FS, GS, SS |
| 5 | Příznakový registr | 1 | 32 bitů | EFLAGS (původně 16bitový FLAGS) |
| 6 | Registry pro ladění | 8 | 32 bitů | DR0..DR7 |
| 7 | Řídicí registry | 4 | 32 bitů | CR0, CR2, CR3, CR4 |
| 8 | Další spec. registry | 12? | 32 bitů | TR1…TR12 |
| 9 | Registry MMX/3DNow! | 8 | 64 bitů | shodné s FPU registry st(x), resp. se spodními 64 bity st(x) |
| 10 | Pracovní registry SSE | 8 | 128 bitů | XMM0 .. XMM7 |
| 11 | Řídicí registr SSE | 1 | 32 bitů | MXCSR |
Obrázek 21: Zjednodušený programátorský model architektury x86 v 32bitovém režimu.
11. Nové instrukce přidané v technologii SSE
V rámci technologie SSE byla instrukční sada x86 (a později x86–64) rozšířena o několik typů instrukcí, které většinou pracovaly s již výše zmíněnými registry XMM*, popř. taktéž s operační pamětí nebo s obecnými celočíselnými 32bitovými registry procesorů x86, tj. například s registrem EAX. Všechny nové instrukce je možné rozdělit do několika kategorií:
| # | Kategorie | Příklad instrukce |
|---|---|---|
| 1 | Přenosy dat | MOVUPS, MOVAPS, MOVHPS, MOVLPS… |
| 2 | Aritmetické operace | ADDPS, SUBPS, MULPS, DIVPS, RCPPS… |
| 3 | Porovnání | CMPEQSS, CMPEQPS, CMPLTSS, CMPNLTSS, … |
| 4 | Logické operace | ANDPS, ANDNPS, ORPS, XORPS |
| 5 | Přenosy mezi prvky vektorů (shuffle) a konverze | SHUFPS, UNPCKHPS, UNPCKLPS |
| 6 | Načtení dat do cache | PREFETCH0, … |
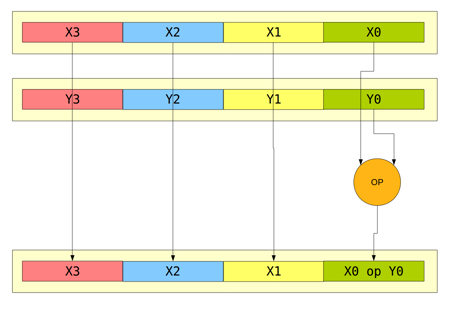
Obrázek 22: Některé instrukce zavedené v rámci SSE pracují pouze s dvojicí skalárních hodnot.
Zajímavá je podpora jak skalárních operací, tak i operací vektorových (přesněji řečeno SIMD) v instrukční sadě SSE. Příkladem může být například skalární instrukce součtu ADDSS (SS=single scalar), která může mít dvojí podobu:
ADDSS xmm1, xmm2 ; instrukce pracující s dvojicí registrů SSE ADDSS xmm1, mem32 ; instrukce pracující s registrem SSE a paměťovým místem (32 bitů)
Naproti tomu „vektorová“ podoba instrukce součtu ADDPS (PS=parallel scalar) pracuje s čtyřprvkovými vektory a zajímavé je, že operační kód této instrukce je o jeden prefixový bajt kratší, než je tomu u dříve zmíněné instrukce ADDSS (to dává smysl, protože častěji používané vektorové instrukce zaberou v operační paměti menší objem, je větší pravděpodobnost jejich načtení z cache atd.):
ADDPS xmm1, xmm2 ; instrukce pracující s dvojicí registrů SSE ADDPS xmm1, mem128 ; instrukce pracující s registrem SSE a paměťovým místem (128 bitů)
Taktéž stojí za zdůraznění fakt, že se v instrukční sadě SSE nenachází žádné instrukce, v jejichž operačním kódu by se nacházela konstanta. Ta musí být vždy uložena v operační paměti nebo přenesena z obecných registrů (což trošku připomíná klasické RISCové procesory).

Obrázek 23: Vektorové operace podporované instrukční sadou SSE.
Nejdůležitější skupinou SSE instrukcí jsou instrukce určené pro provádění aritmetických výpočtů. Tyto instrukce, které jsou vypsány v následující tabulce, pracují buď s dvojicí skalárních hodnot typu float/single umístěných v nejnižších 32 bitech 128bitového registru, nebo naopak s dvojicí vektorů, z nichž každý obsahuje čtyři 32bitové hodnoty opět typu float/single:
| # | Instrukce se skalárními operandy | Instrukce pracující s vektory | Význam instrukce |
|---|---|---|---|
| 1 | ADDSS | ADDPS | součet |
| 2 | SUBSS | SUBPS | rozdíl |
| 3 | MULSS | MULPS | součin |
| 4 | DIVSS | DIVPS | podíl |
| 5 | RCPSS | RCPPS | převrácená hodnota |
| 6 | SQRTSS | SQRTPS | druhá odmocnina |
| 7 | RSQRTSS | RSQRTPS | převrácená hodnota z druhé odmocniny |
| 8 | MAXSS | MAXPS | výpočet maxima |
| 9 | MINSS | MINPS | výpočet minima |

Obrázek 24: Formát 32bitových slov obsahujících hodnoty s plovoucí řádovou čárkou podle IEEE 754 (single/float).
12. Rozšíření instrukční sady SSE2
Poměrně záhy po uvedení instrukční sady SSE se mnozí vývojáři začali ptát, proč se vlastně většina nově přidaných instrukcí omezuje pouze na práci s numerickými hodnotami s jednoduchou přesností, když je mnoho aplikací založených na celočíselných datech (osmibitových bajtech, šestnáctibitových slovech, 32bitových slovech atd.), které by tak mohly využívat všech možností nabízených novými 128bitovými registry technologie SSE. Vývojáři pracující především na vývoji algoritmů z oblasti numerické matematiky by naopak uvítali práci s čísly s dvojitou přesností (double) uloženými v 64 bitech (tj. v případě 128bitových registrů by bylo možné do těchto registrů ukládat dvojice čísel s dvojitou přesností – i to by mohlo představovat významné zvýšení výpočetního výkonu). Odpovědí na oba v podstatě protichůdné požadavky byla instrukční sada pojmenovaná jednoduše SSE2, která pochází z roku 2001. Tato sada byla zpočátku použita v mikroprocesorech Intel Pentium 4 a Intel Xeon, později se však rozšířila i na procesory firmy AMD (Athlon64, Opteron).
Technologie SSE2 vývojářům přinesla nové instrukce a samozřejmě i podstatné změny v interní struktuře vektorové výpočetní jednotky, ovšem počet registrů ani jejich bitová šířka se nijak nezměnila. Programátoři používající, ať již přímo či nepřímo, rozšíření instrukční sady SSE2 mohli do osmice 128bitových registrů pojmenovaných XMM* ukládat celkem šest různých typů vektorů. Základ zůstal nezměněn – jednalo se o čtyřprvkové vektory obsahující čísla reprezentovaná ve formátu plovoucí řádové čárky, přičemž každé číslo bylo uloženo v 32 bitech (4×32=128 bitů), což odpovídá typu single/float definovanému v normě IEEE 754. Kromě toho byly v rámci SSE2 ještě zavedeny dvouprvkové vektory obsahující taktéž hodnoty reprezentované ve formátu plovoucí řádové čárky, ovšem tentokrát se jedná o čísla uložená v 64 bitech (2×64=128) odpovídající dvojité přesnosti (double) z normy IEEE 754.
Zbývají nám ovšem ještě čtyři další podporované datové typy. Jedná se o vektory s celočíselnými prvky: šestnáctiprvkové vektory s osmibitovými hodnotami, osmiprvkové vektory s šestnáctibitovými hodnotami, čtyřprvkové vektory s 32bitovými hodnotami a konečně dvouprvkové vektory s 64bitovými celočíselnými hodnotami.
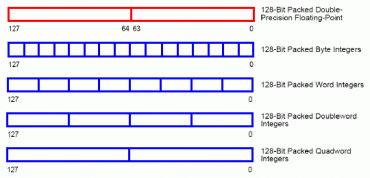
Obrázek 25: Nové typy vektorů, s kterými je nově možné nativně pracovat na mikroprocesorech podporujících technologii SSE2.
Instrukce SSE2 je možné využít i v některých oblastech numerické matematiky, i když je na tomto místě nutné říct, že přímo v SSE2 nejsou podporována čísla s rozšířenou přesností (extended), takže v některých případech může dojít při výpočtech v jednotce SSE2 (a nikoli FPU) ke kumulaci chyb ve výsledku. Nicméně kombinace instrukcí určených pro matematický koprocesor s instrukcemi určenými pro funkční jednotku SSE2 byla možná a v mnoha případech dokonce nutná, protože matematický koprocesor kromě základních aritmetických operací podporuje například i výpočet goniometrických funkcí, logaritmů atd.
13. Nové instrukce přidané v rámci rozšíření instrukční sady SSE2
Zatímco se v rozšiřující instrukční sadě SSE popsané v předchozích kapitolách nachází „pouze“ 70 nových instrukcí, byli tvůrci instrukční sady SSE2 mnohem velkorysejší, protože navrhli a posléze i implementovali hned 144 nových instrukcí, což přibližně odpovídá počtu všech základních instrukcí procesorů x86 (pokud samozřejmě nepočítáme všechny povolené adresní režimy a další instrukce, které byly na tuto architekturu postupně „nabaleny“). Tento velký počet nových instrukcí souvisí jak s jíž zmíněnou podporou šesti datových typů popsaných v předchozí kapitole (včetně více než dvaceti zcela nových konverzních funkcí), tak i s novými režimy přístupu k prvkům uloženým ve vektorech a se zcela novými operacemi, které byly navrženy pro podporu algoritmů pro 3D grafiku a práci s videem. Všechny instrukce, které byly přidány v rozšiřující instrukční sadě SSE2, je možné rozdělit do několika kategorií:
- Aritmetické operace prováděné s celými čísly (včetně součtu a rozdílu se saturací)
- Aritmetické operace prováděné s čísly s plovoucí řádovou čárkou
- Logické operace (některé jsou prováděny pro všech 128 bitů)
- Bitové posuny prvků o různé bitové šířce
- Porovnávací (komparační, relační) operace
- Konverzní funkce
- Konverze prvků uložených ve vektorech (zvýšení či snížení bitové šířky, shuffling apod.)
- Načítání a ukládání dat do operační paměti
- Řízení vyrovnávací paměti (cache)
O těchto instrukcích se zmíníme v navazující kapitole.
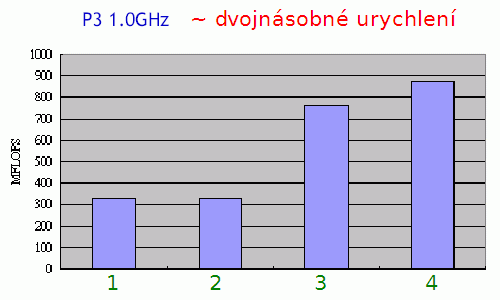
Obrázek 26: Ukázka urychlení operace součtu 1024 číselných prvků reprezentovaných ve formátu s plovoucí řádovou čárkou. Celkem byly použity čtyři algoritmy pro součet:
1 – využití instrukcí FPU
2 – využití instrukcí FPU s rozbalením smyčky
3 – využití vektorových operací SSE/SSE2
4 – využití vektorových operací SSE/SSE2 s rozbalením smyčky
14. Seznam všech instrukcí SSE2
Podobně jako u rozšiřujících instrukčních sad MMX, 3DNow! a SSE, tvoří i u instrukční sady SSE2 nejpodstatnější část nové instrukce určené pro provádění aritmetických operací nad vektory prvků různých datových typů. Všechny nové operace implementované v rámci SSE2 jsou vypsány v následující tabulce. Ve třetím sloupci je naznačeno, jaké vektory jsou danou operací zpracovávány, přičemž první číslo znamená počet prvků vektoru, za nímž následuje bitová šířka jednotlivých prvků:
| # | Instrukce | Operace/funkce | Struktura vektoru | Datový typ | Saturace? | Poznámka |
|---|---|---|---|---|---|---|
| 1 | addpd | součet | 2×64bit | double | × | |
| 2 | addsd | součet | 1×64bit | double | × | operace provedena jen s pravým prvkem vektorů |
| 3 | subpd | rozdíl | 2×64bit | double | × | |
| 4 | subsd | rozdíl | 1×64bit | double | × | operace provedena jen s pravým prvkem vektorů |
| 5 | mulpd | součin | 2×64bit | double | × | |
| 6 | mulsd | součin | 1×64bit | double | × | operace provedena jen s pravým prvkem vektorů |
| 7 | divpd | podíl | 2×64bit | double | × | |
| 8 | divsd | podíl | 1×64bit | double | × | operace provedena jen s pravým prvkem vektorů |
| 9 | paddb | součet | 16×8bit | integer | ne | |
| 10 | paddw | součet | 8×16bit | integer | ne | |
| 11 | paddd | součet | 4×32bit | integer | ne | |
| 12 | paddq | součet | 2×64bit | integer | ne | |
| 13 | paddsb | součet | 16×8bit | integer | ano | |
| 14 | paddsw | součet | 8×16bit | integer | ano | |
| 15 | paddusb | součet | 16×8bit | unsigned | ano | |
| 16 | paddusw | součet | 8×16bit | unsigned | ano | |
| 17 | psubb | rozdíl | 16×8bit | integer | ne | |
| 18 | psubw | rozdíl | 8×16bit | integer | ne | |
| 19 | psubd | rozdíl | 4×32bit | integer | ne | |
| 20 | psubq | rozdíl | 2×64bit | integer | ne | |
| 21 | psubsb | rozdíl | 16×8bit | integer | ano | |
| 22 | psubsw | rozdíl | 8×16bit | integer | ano | |
| 23 | psubusb | rozdíl | 16×8bit | unsigned | ano | |
| 24 | psubusw | rozdíl | 8×16bit | unsigned | ano | |
| 25 | maxpd | maximu | 2×64bit | double | × | |
| 26 | maxsd | maximum | 2×64bit | double | × | operace provedena jen s pravým prvkem vektorů |
| 27 | minpd | minimum | 2×64bit | double | × | |
| 28 | minsd | minimum | 2×64bit | double | × | operace provedena jen s pravým prvkem vektorů |
| 29 | pmaddwd | součin/add | 8×16bit | integer | × | |
| 30 | pmulhw | součin | 8×16bit | integer | × | vrací vektor horních 16 bitů výsledků |
| 31 | pmullw | součin | 8×16bit | integer | × | vrací vektor dolních 16 bitů výsledků |
| 32 | pmuludq | součin | 4×32bit | integer | × | 64 bitový výsledek pro každý součin |
| 33 | rcpps | převrácená hodnota | 4×32bit | single | × | aproximace |
| 34 | rcpss | převrácená hodnota | 4×32bit | single | × | operace provedena jen s pravým prvkem vektorů |
| 35 | sqrtpd | druhá odmocnina | 2×64bit | double | × | |
| 36 | sqrtsd | druhá odmocnina | 2×64bit | double | × | operace provedena jen s pravým prvkem vektorů |
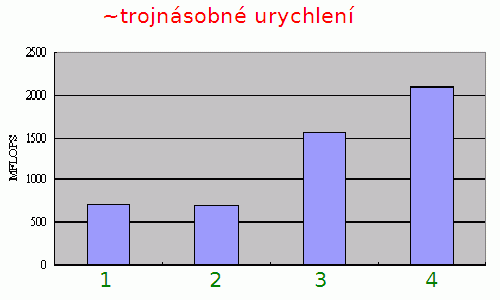
Obrázek 27: Ukázka urychlení operace výpočtu skalárního součinu pro 1024 trojrozměrných vektorů. Prvky vektorů jsou opět reprezentovány ve formátu s plovoucí řádovou čárkou. Celkem byly použity čtyři algoritmy pro součet:
1 – využití instrukcí FPU
2 – využití instrukcí FPU s rozbalením smyčky
3 – využití vektorových operací SSE/SSE2
4 – využití vektorových operací SSE/SSE2 s rozbalením smyčky
Důvod, proč ze došlo k většímu urychlení při použití SSE/SSE2 je jednoduchý: s jednou načtenými daty (vektory) se provádělo větší množství operací, takže se zde v menší míře projevila latence operačních pamětí a další externí vlivy. Sice je možné najít i algoritmy, u nichž je dosaženo ještě většího urychlení výpočtů, ale v praxi je zhruba trojnásobné urychlení (podobně jako na tomto grafu) považováno za velký úspěch.
V instrukční sadě SSE2 můžeme najít i nové logické instrukce a instrukce pro provádění logických či aritmetických posunů. Ve skutečnosti se vlastně jedná o pouhé rozšíření stávajících instrukcí MMX takovým způsobem, aby bylo možné pracovat s novými 128bitovými vektory, popř. s daty uloženými v operační paměti v bloku šestnácti bajtů (16×8=128 bitů). Nejprve si popišme instrukce pro aritmetické a logické posuny. Ty dokážou pracovat s celočíselnými hodnotami o velikosti 16, 32, 64 či 128 bitů, tj. každá část vektoru se posouvá zvlášť (je tedy rozdíl mezi posunem jednoho 128bitového čísla a dvojice 64bitových čísel). Při logických posunech se do nového bitu nasouvá vždy logická nula (nikoli příznak carry), u aritmetických posunů se opakuje hodnota původního nejvyššího bitu, tj. instrukce pracují přesně tak, jak to programátoři očekávají:
| # | Instrukce | Operace/funkce | Struktura vektoru | Datový typ | Poznámka |
|---|---|---|---|---|---|
| 1 | pslldq | logický posun doleva | 1×128bitů | integer | |
| 2 | psllq | logický posun doleva | 2×64bitů | integer | |
| 3 | pslld | logický posun doleva | 4×32bitů | integer | |
| 4 | psllw | logický posun doleva | 8×16bitů | integer | |
| 5 | psrldq | logický posun doprava | 1×128bitů | integer | |
| 6 | psrlq | logický posun doprava | 2×64bitů | integer | |
| 7 | psrld | logický posun doprava | 4×32bitů | integer | |
| 8 | psrlw | logický posun doprava | 8×16bitů | integer | |
| 9 | psrad | aritmetický posun doprava | 4×32bitů | integer | |
| 10 | psraw | aritmetický posun doprava | 8×16bitů | integer |
Následuje seznam instrukcí určených pro provádění logických operací nad vektory různé délky. V některých případech (PAND, POR, PXOR) se jedná o rozšíření původních MMX instrukcí takovým způsobem, aby tyto instrukce mohly pracovat se 128bitovými vektory. Dokonce i operační kódy instrukcí zůstávají stejné, ovšem v případě SSE2 je před vlastním instrukčním kódem uveden prefix 0×66, takže jsou instrukce o jeden bajt delší (to ostatně platí i pro aritmetické operace popsané o několik odstavců výše):
| # | Instrukce | Operace/funkce | Struktura vektoru | Datový typ | Poznámka |
|---|---|---|---|---|---|
| 1 | pand | and | 1×128 bitů | integer | |
| 2 | pandn | not and | 1×128 bitů | integer | první operand je negován |
| 3 | por | or | 1×128 bitů | integer | |
| 4 | pxor | xor | 1×128 bitů | integer | |
| 5 | andpd | and | 2×64 bitů | double | |
| 6 | orpd | or | 2×64 bitů | double | |
| 7 | xorpd | xor | 2×64 bitů | double | |
| 8 | andnpd | not and | 2×64 bitů | double | první operand je negován |
| 9 | andnps | not and | 4×32 bitů | single | první operand je negován |
Při implementaci mnoha algoritmů, především pak při zpracování obrazových a zvukových datových toků, se mnohdy programátoři dostanou do situace, kdy potřebují zkonvertovat data do jiného formátu, než v jakém byla původně uložena. Pro tyto účely jsou v instrukční sadě SSE2 k dispozici dvě desítky konverzních instrukcí začínajících prefixem cvt, vypsaných v tabulce pod tímto odstavcem. Opět platí, že konverze jsou prováděny paralelně:
| # | Instrukce | Konverze z… | Konverze do… |
|---|---|---|---|
| 1 | cvtdq2pd | 2×32bitový integer | 2×64bitový double |
| 2 | cvtdq2ps | 4×32bitový integer | 4×32bitový single |
| 3 | cvtpd2pi | 2×64bitový double | 2×32bitový integer v MMX registru |
| 4 | cvtpd2dq | 2×64bitový double | 2×32bitový integer ve spodní polovině MMX registru |
| 5 | cvtpd2ps | 2×64bitový double | 2×32bitový single ve spodní polovině MMX registru |
| 6 | cvtpi2pd | 2×32bitový integer | 2×32bitový single ve spodní polovině MMX registru |
| 7 | cvtps2dq | 4×32bitový single | 4×32bitový integer |
| 8 | cvtps2pd | 2×32bitový single | 2×64bitový double |
| 9 | cvtsd2si | 1×64bitový double | 1×32bitový integer v pracovním registru (CPU) |
| 10 | cvttpd2pi | 2×64bitový double | 2×32bitový integer (odseknutí desetinné části) |
| 11 | cvttpd2dq | 2×64bitový double | 2×32bitový integer (odseknutí desetinné části) |
| 12 | cvttps2dq | 4×32bitový single | 4×32bitový integer (odseknutí desetinné části) |
| 13 | cvttps2pi | 2×32bitový single | 2×32bitový integer (odseknutí desetinné části) v MMX registru |
| 14 | cvttsd2si | 1×64bitový double | 1×32bitový integer (odseknutí desetinné části) v pracovním registru |
| 15 | cvttss2si | 1×32bitový single | 1×32bitový integer (odseknutí desetinné části) v pracovním registru |
| 16 | cvtsi2sd | 1×32bitový integer | 1×64bitový double |
| 17 | cvtsi2ss | 1×32bitový integer | 1×32bitový single |
| 18 | cvtsd2ss | 1×64bitový double | 1×32bitový single (horní polovina registru se nemění) |
| 19 | cvtss2sd | 1×32bitový single | 1×64bitový double |
| 20 | cvtss2si | 1×32bitový single | 1×32bitový integer v pracovním registru (CPU) |
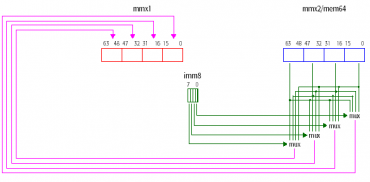
Obrázek 28: Univerzální konverzní funkce PSHUF byla v instrukční sadě SSE2 rozšířena tak, aby dokázala pracovat i se 128bitovými registry.
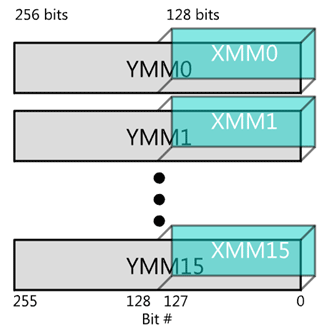
Obrázek 29: V rámci instrukční sady Intel AVX došlo k dalšímu zvýšení bitové šířky „vektorových“ registrů na 256 bitů.
15. Podpora SIMD instrukcí v GCC – vektorová rozšíření
Pokud jste článek dočetli až sem, musíte si asi říkat, jaký instrukční Babylon v oblasti x86/x86–64 vládne. To je pravda a ani vývojářům a ani autorům překladačů to nijak neulehčuje život. Jedno z řešení tohoto stavu spočívá v tom, že překladače začnou podporovat obecné vektorové operace. A jednou z realizací této myšlenky je rozšíření GCC C (a C++) o de facto nové datové typy „vektor určité bajtové délky“.
Podívejme se na následující příklad, v němž je definován nový typ nazvaný v16us (jméno může být pochopitelně jakékoli). Jedná se o vektor o délce šestnácti bajtů, který obsahuje prvky typu short int, což zde konkrétně může znamenat, že se do vektoru vejde celkem osm těchto prvků za předpokladu, že sizeof(unsighed short int)==2:
#include <stdio.h>
typedef unsigned short int v16us __attribute__((vector_size(16)));
int main(void)
{
printf("scalar: %ld bytes\n", sizeof(unsigned short int));
printf("vector: %ld bytes\n", sizeof(v16us));
return 0;
}
Výsledek:
scalar: 2 bytes vector: 16 bytes
Vyzkoušet si můžeme i další vektory o celkové délce 16 bajtů, jejichž prvky budou různých typů a tudíž i délka vektoru měřená v počtu prvků bude odlišná:
#include <stdio.h>
typedef unsigned char v16ub __attribute__((vector_size(16)));
typedef unsigned short int v16us __attribute__((vector_size(16)));
typedef unsigned int v16ui __attribute__((vector_size(16)));
typedef unsigned long int v16ul __attribute__((vector_size(16)));
int main(void)
{
printf("unsigned char: %ld bytes\n", sizeof(unsigned char));
printf("unsigned short: %ld bytes\n", sizeof(unsigned short int));
printf("unsigned int: %ld bytes\n", sizeof(unsigned int));
printf("unsigned long: %ld bytes\n", sizeof(unsigned long int));
printf("vector unsigned char: %ld bytes\n", sizeof(v16ub));
printf("vector unsigned short: %ld bytes\n", sizeof(v16us));
printf("vector unsigned int: %ld bytes\n", sizeof(v16ui));
printf("vector unsigned long: %ld bytes\n", sizeof(v16ul));
return 0;
}
Výsledek:
unsigned char: 1 bytes unsigned short: 2 bytes unsigned int: 4 bytes unsigned long: 8 bytes vector unsigned char: 16 bytes vector unsigned short: 16 bytes vector unsigned int: 16 bytes vector unsigned long: 16 bytes
Totéž platí i pro vektory s prvky se znaménkem:
#include <stdio.h>
typedef signed char v16ub __attribute__((vector_size(16)));
typedef signed short int v16us __attribute__((vector_size(16)));
typedef signed int v16ui __attribute__((vector_size(16)));
typedef signed long int v16ul __attribute__((vector_size(16)));
int main(void)
{
printf("signed char: %ld bytes\n", sizeof(signed char));
printf("signed short: %ld bytes\n", sizeof(signed short int));
printf("signed int: %ld bytes\n", sizeof(signed int));
printf("signed long: %ld bytes\n", sizeof(signed long int));
printf("vector signed char: %ld bytes\n", sizeof(v16ub));
printf("vector signed short: %ld bytes\n", sizeof(v16us));
printf("vector signed int: %ld bytes\n", sizeof(v16ui));
printf("vector signed long: %ld bytes\n", sizeof(v16ul));
return 0;
}
Výsledky:
signed char: 1 bytes signed short: 2 bytes signed int: 4 bytes signed long: 8 bytes vector signed char: 16 bytes vector signed short: 16 bytes vector signed int: 16 bytes vector signed long: 16 bytes
16. Základní aritmetické operace s vektory
S celými vektory lze pochopitelně provádět i základní aritmetické operace, což je ukázáno na dalším příkladu, společně s ukázkou toho, jak se vlastně vektory naplní daty:
typedef unsigned short int v16us __attribute__((vector_size(16)));
int main(void)
{
v16us x = { 1, 2, 3, 4, 5, 6, 7, 8 };
v16us y = { 0xff, 0xff, 0xff, 0xff, 0xff, 0xff, 0xff, 0xff };
v16us z = x + y;
return 0;
}
Překlad s povolením SSE dopadne následovně:
simd04_2.o: file format elf64-x86-64
Disassembly of section .text:
0000000000000000 <main>:
typedef unsigned short int v16us __attribute__((vector_size(16)));
int main(void)
{
0: f3 0f 1e fa endbr64
4: 55 push rbp
5: 48 89 e5 mov rbp,rsp
v16us x = { 1, 2, 3, 4, 5, 6, 7, 8 };
8: 66 0f 6f 05 00 00 00 movdqa xmm0,XMMWORD PTR [rip+0x0]
f: 00
10: 0f 29 45 d0 movaps XMMWORD PTR [rbp-0x30],xmm0
v16us y = { 0xff, 0xff, 0xff, 0xff, 0xff, 0xff, 0xff, 0xff };
14: 66 0f 6f 05 00 00 00 movdqa xmm0,XMMWORD PTR [rip+0x0]
1b: 00
1c: 0f 29 45 e0 movaps XMMWORD PTR [rbp-0x20],xmm0
v16us z = x + y;
20: 66 0f 6f 45 d0 movdqa xmm0,XMMWORD PTR [rbp-0x30]
25: 66 0f fd 45 e0 paddw xmm0,XMMWORD PTR [rbp-0x20]
2a: 0f 29 45 f0 movaps XMMWORD PTR [rbp-0x10],xmm0
return 0;
2e: b8 00 00 00 00 mov eax,0x0
}
33: 5d pop rbp
34: c3 ret
Důležitá je z našeho pohledu instrukce paddw, kterou jsme si již popsali v rámci předchozích kapitol. Tato funkce provede součet dvou vektorů majících čtyři šestnáctibitové prvky, což je přesně ta instrukce, kterou bychom zde očekávali.
Vyzkoušejme si nyní i další typy vektorů:
#include <stdio.h>
typedef signed char v16ub __attribute__((vector_size(16)));
typedef signed short int v16us __attribute__((vector_size(16)));
typedef signed int v16ui __attribute__((vector_size(16)));
typedef signed long int v16ul __attribute__((vector_size(16)));
int main(void)
{
{
v16ub x = { 1, 2, 3, 4, 5, 6, 7, 8 };
v16ub y = { 0xff, 0xff, 0xff, 0xff, 0xff, 0xff, 0xff, 0xff };
v16ub z = x + y;
}
{
v16us x = { 1, 2, 3, 4, 5, 6, 7, 8 };
v16us y = { 0xff, 0xff, 0xff, 0xff, 0xff, 0xff, 0xff, 0xff };
v16us z = x + y;
}
{
v16ui x = { 1, 2, 3, 4 };
v16ui y = { 0xff, 0xff, 0xff, 0xff };
v16ui z = x + y;
}
{
v16ui x = { 1, 2 };
v16ui y = { 0xff, 0xff };
v16ui z = x + y;
}
return 0;
}
Překlad do „vektorového“ kódu se zvýrazněním SIMD instrukcí:
simd04B_2.o: file format elf64-x86-64
Disassembly of section .text:
0000000000000000 <main>:
typedef signed short int v16us __attribute__((vector_size(16)));
typedef signed int v16ui __attribute__((vector_size(16)));
typedef signed long int v16ul __attribute__((vector_size(16)));
int main(void)
{
0: f3 0f 1e fa endbr64
4: 55 push rbp
5: 48 89 e5 mov rbp,rsp
8: 48 83 ec 48 sub rsp,0x48
{
v16ub x = { 1, 2, 3, 4, 5, 6, 7, 8 };
c: 66 0f 6f 05 00 00 00 movdqa xmm0,XMMWORD PTR [rip+0x0]
13: 00
14: 0f 29 85 40 ff ff ff movaps XMMWORD PTR [rbp-0xc0],xmm0
v16ub y = { 0xff, 0xff, 0xff, 0xff, 0xff, 0xff, 0xff, 0xff };
1b: 66 0f 6f 05 00 00 00 movdqa xmm0,XMMWORD PTR [rip+0x0]
22: 00
23: 0f 29 85 50 ff ff ff movaps XMMWORD PTR [rbp-0xb0],xmm0
v16ub z = x + y;
2a: 66 0f 6f 85 40 ff ff movdqa xmm0,XMMWORD PTR [rbp-0xc0]
31: ff
32: 66 0f fc 85 50 ff ff paddb xmm0,XMMWORD PTR [rbp-0xb0]
39: ff
3a: 0f 29 85 60 ff ff ff movaps XMMWORD PTR [rbp-0xa0],xmm0
}
{
v16us x = { 1, 2, 3, 4, 5, 6, 7, 8 };
41: 66 0f 6f 05 00 00 00 movdqa xmm0,XMMWORD PTR [rip+0x0]
48: 00
49: 0f 29 85 70 ff ff ff movaps XMMWORD PTR [rbp-0x90],xmm0
v16us y = { 0xff, 0xff, 0xff, 0xff, 0xff, 0xff, 0xff, 0xff };
50: 66 0f 6f 05 00 00 00 movdqa xmm0,XMMWORD PTR [rip+0x0]
57: 00
58: 0f 29 45 80 movaps XMMWORD PTR [rbp-0x80],xmm0
v16us z = x + y;
5c: 66 0f 6f 85 70 ff ff movdqa xmm0,XMMWORD PTR [rbp-0x90]
63: ff
64: 66 0f fd 45 80 paddw xmm0,XMMWORD PTR [rbp-0x80]
69: 0f 29 45 90 movaps XMMWORD PTR [rbp-0x70],xmm0
}
{
v16ui x = { 1, 2, 3, 4 };
6d: 66 0f 6f 05 00 00 00 movdqa xmm0,XMMWORD PTR [rip+0x0]
74: 00
75: 0f 29 45 a0 movaps XMMWORD PTR [rbp-0x60],xmm0
v16ui y = { 0xff, 0xff, 0xff, 0xff };
79: 66 0f 6f 05 00 00 00 movdqa xmm0,XMMWORD PTR [rip+0x0]
80: 00
81: 0f 29 45 b0 movaps XMMWORD PTR [rbp-0x50],xmm0
v16ui z = x + y;
85: 66 0f 6f 45 a0 movdqa xmm0,XMMWORD PTR [rbp-0x60]
8a: 66 0f fe 45 b0 paddd xmm0,XMMWORD PTR [rbp-0x50]
8f: 0f 29 45 c0 movaps XMMWORD PTR [rbp-0x40],xmm0
}
{
v16ui x = { 1, 2 };
93: 66 0f 6f 05 00 00 00 movdqa xmm0,XMMWORD PTR [rip+0x0]
9a: 00
9b: 0f 29 45 d0 movaps XMMWORD PTR [rbp-0x30],xmm0
v16ui y = { 0xff, 0xff };
9f: 66 0f 6f 05 00 00 00 movdqa xmm0,XMMWORD PTR [rip+0x0]
a6: 00
a7: 0f 29 45 e0 movaps XMMWORD PTR [rbp-0x20],xmm0
v16ui z = x + y;
ab: 66 0f 6f 45 d0 movdqa xmm0,XMMWORD PTR [rbp-0x30]
b0: 66 0f fe 45 e0 paddd xmm0,XMMWORD PTR [rbp-0x20]
b5: 0f 29 45 f0 movaps XMMWORD PTR [rbp-0x10],xmm0
}
return 0;
b9: b8 00 00 00 00 mov eax,0x0
}
be: c9 leave
bf: c3 ret
66 0f fc 85 50 ff ff paddb xmm0,XMMWORD PTR [rbp-0xb0] 66 0f fd 45 80 paddw xmm0,XMMWORD PTR [rbp-0x80] 66 0f fe 45 b0 paddd xmm0,XMMWORD PTR [rbp-0x50] 66 0f fe 45 e0 paddd xmm0,XMMWORD PTR [rbp-0x20]
17. Přístup k prvkům vektorů
V případě potřeby je možné k prvkům vektorů přistupovat tak, jakoby se jednalo o běžné pole:
#include <stdio.h>
typedef unsigned short int v16us __attribute__((vector_size(16)));
int main(void)
{
v16us x = { 1, 2, 3, 4, 5, 6, 7, 8 };
v16us y = { 0xff, 0xff, 0xff, 0xff, 0xff, 0xff, 0xff, 0xff };
v16us z = x + y;
int i;
for (i = 0; i < 8; i++) {
printf("%d %d\n", i, z[i]);
}
return 0;
}
S výsledkem:
0 256 1 257 2 258 3 259 4 260 5 261 6 262 7 263
#include <stdio.h>
typedef unsigned short int v16us __attribute__((vector_size(16)));
int main(void)
{
v16us x = { 1, 2, 3, 4, 5, 6, 7, 8 };
v16us y = { 0xff, 0xff, 0xff, 0xff, 0xff, 0xff, 0xff, 0xff };
v16us z = x + y;
int i;
for (i = 0; i < sizeof(v16us)/sizeof(unsigned short int); i++) {
printf("%d %d\n", i, z[i]);
}
return 0;
}
nebo možná ještě lépe za:
#include <stdio.h>
typedef unsigned short int item;
typedef item v16us __attribute__((vector_size(16)));
int main(void)
{
v16us x = { 1, 2, 3, 4, 5, 6, 7, 8 };
v16us y = { 0xff, 0xff, 0xff, 0xff, 0xff, 0xff, 0xff, 0xff };
v16us z = x + y;
int i;
for (i = 0; i < sizeof(v16us)/sizeof(item); i++) {
printf("%d %d\n", i, z[i]);
}
return 0;
}
18. Vektory s hodnotami s plovoucí řádovou čárkou
Vektory mohou být tvořeny i prvky s numerickými hodnotami s plovoucí řádovou čárkou, tedy konkrétně hodnotami typu single/float a double. Šířku těchto datových typů si můžeme velmi snadno ověřit:
#include <stdio.h>
typedef float v16f __attribute__((vector_size(16)));
typedef double v16d __attribute__((vector_size(16)));
int main(void)
{
printf("scalar float: %ld bytes\n", sizeof(float));
printf("vector float: %ld bytes\n", sizeof(v16f));
printf("scalar double: %ld bytes\n", sizeof(double));
printf("vector double: %ld bytes\n", sizeof(v16d));
return 0;
}
Z výpočtů je patrné, že první vektor bude obsahovat čtyři prvky typu float a druhý vektor dva prvky typu double:
scalar float: 4 bytes vector float: 16 bytes scalar double: 8 bytes vector double: 16 bytes
Pokusme se nyní sečíst dva čtyřprvkové vektory:
typedef float v16f __attribute__((vector_size(16)));
int main(void)
{
v16f x = { 1, 2, 3, 4 };
v16f y = { 0.1, 0.1, 0.1, 0.1 };
v16f z = x + y;
return 0;
}
Pokud povolíme SSE při překladu (dnes výchozí nastavení), bude výsledek tento:
simd07_2.o: file format elf64-x86-64
Disassembly of section .text:
0000000000000000 <main>:
typedef float v16f __attribute__((vector_size(16)));
int main(void)
{
0: f3 0f 1e fa endbr64
4: 55 push rbp
5: 48 89 e5 mov rbp,rsp
v16f x = { 1, 2, 3, 4 };
8: 0f 28 05 00 00 00 00 movaps xmm0,XMMWORD PTR [rip+0x0]
f: 0f 29 45 d0 movaps XMMWORD PTR [rbp-0x30],xmm0
v16f y = { 0.1, 0.1, 0.1, 0.1 };
13: 0f 28 05 00 00 00 00 movaps xmm0,XMMWORD PTR [rip+0x0]
1a: 0f 29 45 e0 movaps XMMWORD PTR [rbp-0x20],xmm0
v16f z = x + y;
1e: 0f 28 45 d0 movaps xmm0,XMMWORD PTR [rbp-0x30]
22: 0f 58 45 e0 addps xmm0,XMMWORD PTR [rbp-0x20]
26: 0f 29 45 f0 movaps XMMWORD PTR [rbp-0x10],xmm0
return 0;
2a: b8 00 00 00 00 mov eax,0x0
}
2f: 5d pop rbp
30: c3 ret
Použita je zde instrukce ADDPS neboli „add parallel-scalar“, která pracuje s čtyřprvkovými vektory. Tato instrukce je zakódována na pouhých čtyřech bajtech, což je na platformě x86–64 úspěch :-)
Podobný příklad, ovšem se čtyřprvkovým vektorem, kde prvky jsou typu double:
typedef double v16d __attribute__((vector_size(16)));
int main(void)
{
v16d x = { 1, 2 };
v16d y = { 0.1, 0.1 };
v16d z = x + y;
return 0;
}
Výsledek překladu do assembleru:
simd08_2.o: file format elf64-x86-64
Disassembly of section .text:
0000000000000000 <main>:
typedef double v16d __attribute__((vector_size(16)));
int main(void)
{
0: f3 0f 1e fa endbr64
4: 55 push rbp
5: 48 89 e5 mov rbp,rsp
v16d x = { 1, 2 };
8: 66 0f 28 05 00 00 00 movapd xmm0,XMMWORD PTR [rip+0x0]
f: 00
10: 0f 29 45 d0 movaps XMMWORD PTR [rbp-0x30],xmm0
v16d y = { 0.1, 0.1 };
14: 66 0f 28 05 00 00 00 movapd xmm0,XMMWORD PTR [rip+0x0]
1b: 00
1c: 0f 29 45 e0 movaps XMMWORD PTR [rbp-0x20],xmm0
v16d z = x + y;
20: 66 0f 28 45 d0 movapd xmm0,XMMWORD PTR [rbp-0x30]
25: 66 0f 58 45 e0 addpd xmm0,XMMWORD PTR [rbp-0x20]
2a: 0f 29 45 f0 movaps XMMWORD PTR [rbp-0x10],xmm0
return 0;
2e: b8 00 00 00 00 mov eax,0x0
}
33: 5d pop rbp
34: c3 ret
Zde je použita instrukce addpd, což je obdoba addps, ovšem pro prvky typu double a nikoli float/single
19. Repositář s demonstračními příklady
Demonstrační příklady napsané v jazyku C, které jsou určené pro překlad pomocí překladače GCC C, byly uložen do Git repositáře, který je dostupný na adrese https://github.com/tisnik/presentations. Jednotlivé demonstrační příklady si můžete v případě potřeby stáhnout i jednotlivě bez nutnosti klonovat celý (dnes již velmi rozsáhlý) repositář:
20. Odkazy na Internetu
- GCC documentation: Extensions to the C Language Family
https://gcc.gnu.org/onlinedocs/gcc/C-Extensions.html#C-Extensions - GCC documentation: Using Vector Instructions through Built-in Functions
https://gcc.gnu.org/onlinedocs/gcc/Vector-Extensions.html - SSE (Streaming SIMD Extentions)
http://www.songho.ca/misc/sse/sse.html - Timothy A. Chagnon: SSE and SSE2
http://www.cs.drexel.edu/~tc365/mpi-wht/sse.pdf - Intel corporation: Extending the Worldr's Most Popular Processor Architecture
http://download.intel.com/technology/architecture/new-instructions-paper.pdf - SIMD architectures:
http://arstechnica.com/old/content/2000/03/simd.ars/ - Tour of the Black Holes of Computing!: Floating Point
http://www.cs.hmc.edu/~geoff/classes/hmc.cs105…/slides/class02_floats.ppt - 3Dnow! Technology Manual
AMD Inc., 2000 - Intel MMXTM Technology Overview
Intel corporation, 1996 - MultiMedia eXtensions
http://softpixel.com/~cwright/programming/simd/mmx.phpi - AMD K5 („K5“ / „5k86“)
http://www.pcguide.com/ref/cpu/fam/g5K5-c.html - Sixth Generation Processors
http://www.pcguide.com/ref/cpu/fam/g6.htm - Great Microprocessors of the Past and Present
http://www.cpushack.com/CPU/cpu1.html - Very long instruction word (Wikipedia)
http://en.wikipedia.org/wiki/Very_long_instruction_word - CPU design (Wikipedia)
http://en.wikipedia.org/wiki/CPU_design - Bulldozer (microarchitecture)
https://en.wikipedia.org/wiki/Bulldozer_(microarchitecture)






































