Obsah
1. Středový stochastický fraktál
2. První demonstrační příklad – všesměrová difúze
3. Druhý demonstrační příklad – odstranění sub-boxů
4. Ukázky trajektorie částic před jejich dotykem a následným splynutím s obrazcem difúze
5. Shrnutí metod vytvořených pro simulaci difúze
6. Literatura a odkazy na Internetu
7. Obsah dalšího pokračování tohoto seriálu
1. Středový stochastický fraktál
V předchozí části tohoto seriálu jsme si popsali algoritmus, který sloužil pro vytváření realistických modelů zejména vývojově nižších rostlin. Tento algoritmus je možné jednoduše upravit tak, aby se zobrazoval takzvaný středový stochastický fraktál, což je obrazec větvícího se objektu, který vychází z jediného bodu – svého středu. Tento obrazec, který v mnoha ohledech nejvíce odpovídá reálné difúzi kapky jedné kapaliny v kapalině jiných fyzikálních vlastností (chemici a fyzikové tento útvar jistě ihned rozpoznají), se dá získat třemi úpravami minule popsaného algoritmu difúze:
- První úprava spočívá v tom, že se okolí Ω0, ve kterém probíhá generování nové částice při inicializaci algoritmu, nastaví na jediný bod P0, který se nachází ve středu bitmapy (2D případ) či objemové prostorové mřížky (3D případ). S přibývajícím počtem bodů, resp. částic na vznikajícím obrazci, se však okolí postupně zvětšuje a nabývá tvaru kružnice v ploše E2 či koule v prostoru E3. Tato kružnice či koule má střed právě v bodu P0.
- Druhou úpravou se mění tvar okolí Ω‚, ve kterém mohou ležet trajektorie pohybujících se částic. Toto okolí má tvar kružnice v E2 či koule v E3 a postupně se zvětšuje tak, aby kopírovalo rostoucí velikost generovaného fraktálního obrazce. Vždy však musí platit, že oblast generování nových částic Ω0 musí celá ležet uvnitř oblasti, ve které se mohou částice pohybovat Ω‘. Současně musí obě tyto oblasti ležet v prostoru Ω, který omezuje vznikající fraktální obrazec – tato oblast má většinou tvar obdélníka, resp. kvádru, svou velikostí odpovídajícího požadované velikosti fraktálu.
- Třetí úprava původního algoritmu spočívá v realizaci změny velikosti a tvaru okolí Ω0. S tím, jak fraktální obrazec roste z počátečního bodu P0, se mění i okolí, jež má v E2 tvar mezikruží a v E3 se jedná o prostor mezi dvojicí koulí s nestejnými poloměry r1 a r2. Kružnice či koule s menším poloměrem určuje místa generování nových částic, kružnice/koule s poloměrem větším pak hranici, kterou částice při svém pohybu nesmí překročit – tato podmínka vede k významnému urychlení generování fraktálního obrazce.
Obrázek 1: Oblasti generování středového stochastického fraktálu (autor D. Makovský)
S tím, jak velikost fraktálního objektu roste, se zvětšuje i okolí Ω‚, ve kterém se mohou částice pohybovat. To také způsobuje postupné zpomalování generování fraktálního objektu, protože se zmenšuje pravděpodobnost protnutí trajektorie částice se stávajícím objektem. Z tohoto důvodu je možné výše uvedené tři modifikace změnit tak, aby plocha, S resp. objem O okolí Ω‘, zůstával konstantní. Ukázka fraktálního objektu, který vznikl aplikací algoritmu pozměněného podle výše uvedených bodů, je zobrazena na následujícím ilustračním obrázku.

Obrázek 2: Ukázka středového stochastického fraktálu vzniklého aplikací algoritmu difúze
Malou úpravou předchozího algoritmu je možné dosáhnou jiného tvaru generovaného fraktálu. Změna spočívá v tom, že se tvar okolí změní z kružnice na čtverec.

Obrázek 3: Středový stochastický fraktál vytvářený v okolí tvaru čtverce
2. První demonstrační příklad – všesměrová difúze
Algoritmus, který je uveden v této kapitole, je určen pro vytváření rastrového obrazu všesměrové difúze, tj. takového obrazce difúze, který vyrůstá z jednoho bodu (semínka) do všech směrů tak, že ve všech směrech tvoří statisticky symetrický objekt. Svojí podstatou se postup generování obrazu difúze podobá postupu, při kterém se vytvářely sub-boxy ve větším posuvném boxu. Podstatný rozdíl však spočívá v tom, že původní posuvný box je nahrazen mezikružím, jehož střed je umístěn ve středu oblasti, ze které fraktální obrazec vyrůstá a vnější i vnitřní poloměr tohoto mezikruží se neustále zvětšuje spolu s rostoucím obrazcem difúze.
Podobně jako u algoritmu realizovaného ve čtvrtém demonstračním příkladu (nazvaném Diffuse4 a uvedeném v předchozí části tohoto seriálu) se při běhu zde popisovaného algoritmu postupně generují body v ploše E2 a pro každý takto vygenerovaný bod je před jeho připojením k obrazci difúze prováděn test, zda obraz tohoto bodu v pracovní bitmapě či pixmapě (tj. pixel) neleží ve čtyřokolí nebo osmiokolí pixelů náležejících do stávajícího fraktálního obrazce představujícího všesměrovou difúzi. Převod tohoto algoritmu z plochy E2 do trojrozměrného prostoru E3 je možný pouze za předpokladu, že se sub-boxy nahradí osově orientovanými kvádry, které nevznikají ve zvětšujícím se mezikruží, ale v prostoru, jenž se nachází mezi plochami dvou koulí se shodným středem.
Počet sub-boxů, které se při každém zvětšení poloměru mezikruží vytvoří, je parametricky zadáván uživatelem pomocí posuvného ovládacího prvku Box count. Čím větší je počet sub-boxů, tím rovnoměrněji budou jednotlivé větve obrazce difúze generovány, protože se (alespoň statisticky) zvyšuje i pokrytí celého mezikruží sub-boxy. Celkový počet bodů vytvořených v každém sub-boxu je taktéž zadáván uživatelem pomocí scroll baru Sub-boxes. Vyšší počet bodů v každém sub-boxu má za následek větší lokální hustotu bodů v obrazci difúze; rovnoměrnost větví ani globální hustota celého obrazce však není tímto parametrem prakticky vůbec ovlivněna.
Posledním význačným parametrem, jež úzce souvisí se sub-boxy a jejich vlivu na hustotu vytvářeného fraktálního útvaru, je jejich velikost, která je nastavovaná pomocí posuvného ovládacího prvku Sub-box size. Čím je velikost sub-boxů větší, tím menší je lokální hustota bodů, protože se zmenšuje pravděpodobnost dotyku vygenerovaného bodu se stávajícím obrazcem difúze. Na druhou stranu se ovšem zvyšuje symetrie vytvářeného obrazce, protože u zvětšujících se sub-boxů dochází, alespoň v prvních iteracích kdy je poloměr kružnice/koule malý, k jejich částečnému překrytí.
Překlad aplikace do bytekódu jazyka Java se provede zadáním následujícího příkazu:
javac Diffuse6.java Pro potřeby spuštění aplikace na starších JRE (například v prohlížeči Internet Explorer) je možné specifikovat cílovou verzi virtuálního stroje jazyka Java pomocí přepínače target:
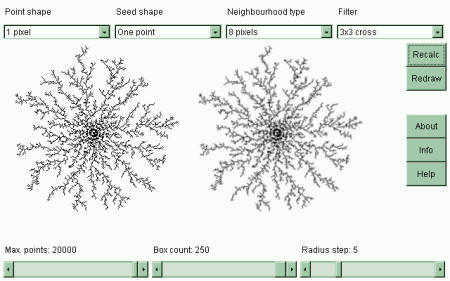
javac -target 1.1 Diffuse6.java Obrázek 4: Screenshot prvního demonstračního příkladu
Zdrojový kód tohoto demonstračního příkladu je dostupný jak ve formě plaintextu, tak i jako HTML stránka se zvýrazněnou syntaxí.
Metoda, která aplikuje výše uvedenou modifikaci algoritmu difúze, má následující tvar:
// -----------------------------------------------------------------------
// Vlastní aplikace šestého algoritmu difúze založeného na postupném
// připojování bodů směrem od středu pomocné bitmapy. Body jsou generovány
// v plochách vytvářených ve zvětšujících se mezikružích.
// -----------------------------------------------------------------------
private void applyDiffuse() {
final int CounterThreshold=200; // počet bodů pro provedení výpisu
// do GUI okna appletu či aplikace
int counter=0; // počitadlo vytvořených bodů
int points=0; // počitadlo všech bodů
int dist; // vzdálenost bodu od středu kružnice
float alpha; // úhel vytvořeného bodu
int xb, yb;
int x, y, xi, yi; // souřadnice generovaných bodů
int box, subbox; // počitadla smyček
int originX=width>>1; // souřadnice středu bitmapy
int originY=height>>1;
int radius; // maximální poloměr kružnice
float subBoxHalf=(float)(subBoxSize/2.0);// poloviční velikost sub-boxů
if (originX<originY) // výpočet maximálního poloměru
radius=originX; // kružnice, ve které se vytváří
else // sub-boxy, z rozměrů pracovní bitmapy
radius=originY;
putPoint(originX, originY); // vytvořit bod ve středu obrazce
// (tento bod je součástí semínka)
// hlavní programová smyčka, ve které se provádí připojení jednotlivých bodů k obrazci
for (dist=0; dist<radius-1; dist++) {
box=0;
// smyčka pro vygenerování zadaného počtu boxů
while (box<boxCount) {
// úhel odchylky středu boxů
alpha=(float)(Math.random()*2.0*Math.PI);
// souřadnice levého horního rohu oblasti,
// ve které se budou vytvářet nové body
xb=(int)(originX+dist*Math.cos(alpha)-subBoxHalf);
yb=(int)(originY+dist*Math.sin(alpha)-subBoxHalf);
// smyčka pro vytvoření zadaného počtu sub-boxů
// a bodů v sub-boxech
for (subbox=0; subbox<subBoxCount; subbox++) {
x=(int)(Math.random()*subBoxSize); // relativní souřadnice bodu v boxu
y=(int)(Math.random()*subBoxSize);
xi=x+xb; // výpočet absolutních souřadnic nového bodu
yi=y+yb;
// pokud se nový bod dotkne stávajícího objektu
if (neighboor(neighboorType, x+xb, y+yb)) {
putPoint(x+xb, y+yb); // připojit bod k objektu
points++; // zvýšit počitadlo všech připojených bodů
box++;
if (points>maxPoints) // ukončit výpočet po překročení
return; // zadaného počtu bodů
break;
}
counter++;
if (counter==CounterThreshold) {// po dosažení dostatečného počtu bodů
label.setText("Points: " // zapsat informace do GUI okna appletu
+String.valueOf(points) // či aplikace
+" box: "
+String.valueOf(box)
+" distance: "
+String.valueOf(dist));
counter=0;
}
} // konec smyčky, ve které se vytvářely nové body
} // konec smyčky s generováním oblastí
} // konec hlavní programové smyčky
}
3. Druhý demonstrační příklad – odstranění sub-boxů
Algoritmus všesměrové difúze, tj. difúze vycházející z jediného bodu (semínka) a rostoucí statisticky pravidelně do všech směrů, který byl popsán v první kapitole (a implementován v předchozím demonstračním příkladu), lze účelně modifikovat tak, že se změní metoda používaná pro vytváření a připojování nových bodů ke vznikajícímu obrazci difúze. U předešlého algoritmu se ve vnější programové smyčce postupně zvětšoval poloměr mezikruží, ve kterém se vytvářely sub-boxy, v jejichž ploše se následně ve vnitřní programové smyčce generovaly body na náhodné pozici. Tyto body byly při dotyku s rastrovým obrazcem difúze k tomuto obrazci připojeny.
Postup použitý u předchozího algoritmu lze upravit tak, aby nebylo zapotřebí vytvářet a uživatelsky parametrizovat ani velikost mezikruží ani další parametry sub-boxů. Modifikace spočívá v odlišném způsobu vytváření a následném pohybu bodů, které se mají připojit ke vznikajícímu rastrovému obrazci reprezentujícímu difúzi v pracovní bitmapě. Body se nyní nevytváří v sub-boxech, ale na kružnici, jejíž střed leží na souřadnicích semínka a poloměr se postupně zvětšuje od nejnižší hodnoty (zadané uživatelem) směrem k hodnotě nejvyšší, která je vypočtena na základě velikosti pracovní bitmapy či pixmapy a současně poloze semínka v této pracovní oblasti.
Rychlost zvětšování kružnice, tj. hodnota, o kterou se v každém kroku vnější programové smyčky zvětší poloměr kružnice, je možné uživatelsky změnit pomocí posuvného ovládacího prvku Radius Step. To, že body vznikají na postupně se zvětšující kružnici a nikoli náhodně po celé ploše omezené velikostí pracovní bitmapy, přispívá k urychlení výpočtů, protože se zvyšuje pravděpodobnost dotyku bodu s obrazcem; také se zvětšuje symetričnost tvaru a hustoty vygenerovaného obrazce difúze.
Bod je na předem vypočtené kružnici vytvořen na náhodném místě, které je možné reprezentovat jedním parametrem, například úhlem odklonu spojnice bodu se semínkem od kladné horizontální poloosy. Po výpočtu pozice bodu na kružnici se pozice bodu převedou na souřadnice pixelu (dojde tedy k zaokrouhlení obou souřadnic na nejbližší celá čísla) a bod se začne v pracovní bitmapě či pixmapě pohybovat stejně, jako tomu bylo u předchozího algoritmu.
Vzhledem k tomu, že obraz difúze má vycházet z jednoho bodu, musí být v semínku obsažen i pixel, jež se nachází ve středu pracovní bitmapy. Ostatní body semínka jsou volitelné pomocí výběrového boxu Seed shape.
V každém výpočetním kroku programové smyčky zajišťující pohyb bodu se tedy změní jedna nebo obě souřadnice bodu, vždy však pouze o jednotku, tj. maximálně o jeden pixel ve vertikálním a/nebo horizontálním směru. Nová souřadnice bodu Xn+1=(xn+1, yn+1) v bitmapě se tedy nachází v osmiokolí souřadnice bodu Xn=(xn, yn) z předchozího kroku. Pokud se bod Xn+1 na nové souřadnici dotkne stávajícího fraktálního objektu, je k tomuto objektu připojen, vnitřní programová smyčka ukončena a následně jsou vypočteny souřadnice, ze kterých se začne pohybovat další bod, jenž je adeptem na připojení ke vznikajícímu fraktálnímu objektu.
Překlad aplikace do bytekódu jazyka Java se provede zadáním následujícího příkazu:
javac Diffuse7.java Opět je možné, stejně jako ve všech předchozích Javovských demonstračních aplikacích, specifikovat cílovou verzi virtuálního stroje jazyka Java:
javac -target 1.1 Diffuse7.java Obrázek 5: Screenshot druhého demonstračního příkladu
Zdrojový kód druhého demonstračního příkladu je dostupný jak ve formě plaintextu, tak i jako HTML stránka se zvýrazněnou syntaxí.
Metoda, která aplikuje výše uvedenou modifikaci algoritmu difúze, má následující tvar:
// -----------------------------------------------------------------------
// Aplikace algoritmu difúze, jenž je založen na postupném pohybu bodů
// v pracovní bitmapě (binární rastrové mřížce). Počáteční pozice bodů
// leží na kružnici, která se při běhu algoritmu plynule zvětšuje od
// středu vznikajícího obrazce difúze až do okrajů vytvářené bitmapy.
// -----------------------------------------------------------------------
private void applyDiffuse() {
final int CounterThreshold=200; // počet bodů pro provedení výpisu
// do GUI okna appletu či aplikace
int counter=0; // počitadlo vytvořených bodů
int points=0; // počitadlo všech bodů
int dist; // vzdálenost od středu obrazce
float alpha; // úhel vytvořeného bodu od x-ové osy
int x, y; // souřadnice generovaných bodů
int box; // počitadla smyček
int originX=width>>1; // souřadnice středu pracovní bitmapy
int originY=height>>1;
int radius; // maximální povolený poloměr kružnice
boolean looking;
if (originX<originY) // výpočet maximálního povoleného
radius=originX; // poloměru kružnice z rozměrů
else // pracovní bitmapy
radius=originY;
putPoint(originX, originY); // vytvořit bod ve středu obrazce
// (tento bod je vždy součástí semínka)
// hlavní programová smyčka, jež obstarává změnu velikosti kružnice, na které se
for (dist=0; dist<radius-1; dist+=radiusStep) { // vytváří počáteční pozice bodu
box=0;
// vnitřní smyčka pro vygenerování zadaného počtu bodů na kružnici
while (box<boxCount) {
// úhel odchylky měřený od horizontální osy
alpha=(float)(Math.random()*2.0*Math.PI);
// souřadnice levého horního rohu oblasti
// převedeného na pixely
x=(int)(originX+dist*Math.cos(alpha));
y=(int)(originY+dist*Math.sin(alpha));
looking=true; // nastavit příznak hledání bodů
// vnitřní smyčka pro nalezení místa připojení pixelů k obrazci difúze
do {
x+=Math.random()*3.0-1; // posun pixelu v ploše
y+=Math.random()*3.0-1; // na jeho osmiokolí
if (x<1) x++; // kontrola, zda pixel
if (x>width-2) x--; // leží uvnitř povolené
if (y<1) y++; // oblasti v bitmapě
if (y>height-2) y--;
// pokud se pixel dotkl stávajícího objektu
if (neighboor(neighboorType, x, y)){
putPoint(x, y); // je k němu připojen
looking=false; // hledání lze ukončit
points++; // zvýšit počitadlo všech připojených bodů
box++;
}
// po dosažení dostatečného počtu připojených pixelů
counter++; // průběžný výpis práce programu
if (counter==CounterThreshold) {
label.setText("Points: " // do GUI okna appletu či aplikace
+String.valueOf(points)
+" dist: "
+String.valueOf(dist));
counter=0;
}
} while (looking); // interní smyčku ukončit až po připojení
} // pixelu k obrazci difúze
} // konec hlavní programové smyčky
} 
Obrázek 6: Fraktál vytvořený pomocí druhého demonstračního příkladu
4. Ukázky trajektorie částic před jejich dotykem a následným splynutím s obrazcem difúze
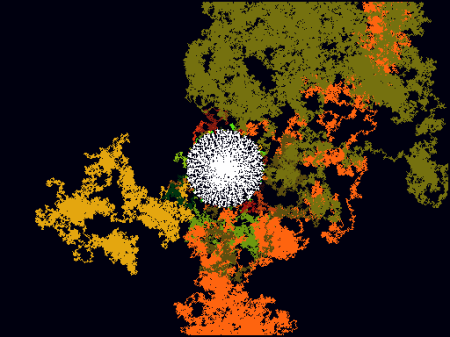
Abychom si udělali rámcovou představu o tom, kolik práce musí počítač vykonat při výpočtu tvaru středové difúze, vytvořil jsem několik obrázků, na kterých jsou ukázány trajektorie částic před jejich připojením do objektu difúze. Na obrázcích 7–10 je bílou barvou naznačen vytvářený fraktál, barva černá je barvou okolí. Pomocí dalších barvových odstínů jsou zobrazeny (osmispojité) trajektorie částic z místa jejich vzniku až do místa dotyku s rostoucím objektem difúze. Na obrázcích 11 a 12 jsou naproti tomu znázorněny „hustoty“ trajektorií; v místech, kde se více trajektorií protíná, se zvyšuje intenzita žluté barvy.
Obrázek 7: Trajektorie několika částic pro podmínky: radius=20, boxCount=100
Obrázek 8: Trajektorie několika částic pro podmínky: radius=50, boxCount=100
Obrázek 9: Trajektorie několika částic pro podmínky: radius=50, boxCount=50
Obrázek 10: Trajektorie několika částic pro podmínky: radius=100, boxCount=100
Obrázek 11: Hustota trajektorií několika částic
Obrázek 12: Hustota trajektorií většího množství částic
5. Shrnutí metod vytvořených pro simulaci difúze
V posledních čtyřech pokračováních tohoto seriálu jsem popsal metody, pomocí nichž je možné na základě iterativního výpočtu, vytvářet tvarově složité přírodní útvary, zejména modely stromů, keřů nebo trávy. Vytvořené modely se vyznačují fraktální strukturou a soběpodobností. Vzhledem ke značné tvarové složitosti vytvořených modelů je prakticky nemožné, aby byly reprezentovány některou z konvenčních metod reprezentace těles (tj. plošné polygony resp. trojúhelníky). Ukazuje se, že i takto vytvořené modely je vhodné ukládat ve formě množiny bodů, částic či surfelů, podobně jako modely vytvořené pomocí systémů iterovaných funkcí IFS a linearizovaných systémů iterovaných funkcí L-IFS – viz předchozí části tohoto seriálu (XXX – XXXIX).
Z důvodu snadné modifikace tvaru a celkové charakteristiky generovaného objektu jsem také navrhl a popsal několik způsobů, jakým lze původní algoritmus simulace difúze upravit. Úpravy spočívají jak v odlišném zadání počátečních podmínek, tak i ve specifikaci prostoru (Ω, Ω'), ve kterém se mohou nové částice generovat a případně i pohybovat. Změnou omezujících podmínek se provádí přeměna větší části vygenerovaných objektů, zatímco odlišným nastavením parametrů algoritmu difúze se mění jak celkový vzhled modelu (volba umístění semínek), tak i lokální hustota a charakter vytvářených tvarů (typ/tvar okolí, ve kterém se hledají částice nacházející se uvnitř fraktálního objektu).
6. Literatura a odkazy na Internetu
- Barnsley Michael, Devaney R. L., Mandelbrot Benoit B., Peitgenn Heinz-Otto, Saupe Dietmar, Voss Richard: <i>The Science of Fractal Images</i>,
Springer-Verlag, New York, 1988 - Bowman Richard L.: <i>Fractal Metamorphosis: A Brief Student Tutorial</i>,
Computer and Graphics, 19, strany 157–164, 1995 - Devaney Robert L.: <i>A First Course In Chaotic Dynamical Systems</i>,
Addison-Wesley, Reading, MA, 1992 - Gleick James: Chaos: Making a New Science,
Viking Press, Penguin, New York, 1987 - Gleick James: <i>Chaos: Vznik nové vědy</i> (český překlad předchozí knihy),
Ando Publishing, Brno, 1996 - Makovský Dušan: <i>Stochastické fraktály</i>,
Diplomová práce, VUT FIT Brno, 2003 - Pritchard Joe: <i>The Chaos Cookbook: A Practical Programming Guide</i>,
Butterworth-Heinemann, Oxford, 1992, ISBN 0–7506–0304–6 - Mandelbrot Benoit B.: <i>The Fractal Geometry of Nature</i>,
W. H. Freeman, New York; San Francisco, 1982, ISBN 0–7167–1186–9 - Wegner Timothy, Peterson Mark: <i>Fractal Creations, First Edition</i>,
The Waite Group Press, 1991 - Wegner Timothy, Tyler Bert: <i>Fractal Creations, Second Edition</i>,
The Waite Group Press, 1993 - Wegner Timothy, Tyler Bert, Peterson Mark, Branderhorst Pierer: <i>Fractals for Windows</i>,
The Waite Group Press, 1992 - Žára J., Beneš B., Felkel P.: <i>Moderní počítačová grafika</i>,
Computer Press, Praha, 1998, ISBN 80–7226–049–9 - Žára J., Limpouch A., Beneš B., Werner T.: <i>Počítačová grafika – principy a algoritmy</i>,
Grada, 1992
7. Obsah dalšího pokračování tohoto seriálu
V následujícím pokračování tohoto seriálu se zaměříme na další (a v praxi mnohem častěji používaný) typ stochastických fraktálů. Bude se jednat o objekty vytvářené metodou přesouvání prostředního bodu (Midpoint Displacement Method) v ploše i prostoru.