Když se Wolfram Alpha (někdy také Wolfram|Alpha) objevil, mluvilo se o nástupu sémantického webu. Postupem času se ale ukázalo, že se tento nástroj rozhodl jít poněkud odlišnou cestou. V zásadě jsou zde dvě oblasti funkcionality – znalostí vyhledávání a jeho analýza a CAS. Jelikož nám jde především o oblast výpočtů, o znalostním vyhledávání se příliš zmiňovat nebudeme, jen jako příklad můžeme uvést že si poradí s dotazy typu kolik vyhrálo Československo medailí na olympiádě v Calgary.
Mimo tyto dva hlavní proudy zájmu pak leží celá řadu různých drobností, jako například interpret jazyka funkcionálního paradigmatu, což by mohlo být užitečné i pro některé výpočty. Konec konců právě pro ně je funkcionální programování poměrně silným a užitečným nástrojem.
Pro základní seznámení s možnostmi a syntaxí slouží poměrně podrobně a pěkně zpracovaný seznam příkladů. Užívání tohoto nástroje se příliš neliší od běžných CAS, jen je potřeba počítat s omezeními spojenými s tím, že se jedná o online nástroj. Předně je to poněkud menší rychlost, omezená možnost se vracet k předchozím výpočtům nebo celkově slabší výpočetní možnosti. Wolfram Alpha se nesnaží konkurovat Matlabu, ale spíše je doplňkem k MAPLE či Mathematica.
Velkou výhodou je pak to, že nástroj je zdarma dostupný odkudkoli, kde je Internet – lze ho tedy využívat i na mobilních zařízeních, kde je výběr CAS poněkud omezený. K dispozici je za drobný příplatek i vylepšené prostředí pro iPhone či iPad, který v něm optimalizuje zobrazení informací a celkovou práci se systémem. Pro pravidelné používání rozhodně doporučuji zakoupit.
Zajímavý je přístup aplikace k zobrazování výsledků a informací. Systém se snaží poskytnout nejen výsledek, ale také maximum doplňujících informací, které mohou být uživatelům prospěšné. Nejčastěji se jedná o grafy funkcí, výsledky v alternativním tvaru nebo informace o tom, jak bylo výsledku dosaženo, o definičních oborech a oborech hodnot funkcí atp. Uživatel tak získá z jednoho místa poměrně ucelený přehled o problému, který zadal Wolfram Alpha k řešení. Právě tato komplexnost a uživatelská přístupnost z něj dělá stále populárnější nástroj – celá řadu uživatelů totiž často ani neví, co přesně chce zjistit, řeší domácí úlohy nebo jen chce získat celistvější přehled o dané problematice.
I přes výše zmíněnou chválu se ale pro profesionální používání příliš nehodí, neboť jeho možnosti jsou poněkud omezené a pokročilejší věci si člověk musí udělat sám. Příkladem za všechny je regrese dat – systém vypočítá rovnici, ale nikoli chybu. Tu si již člověk musí určit sám pomocí metody nejmenších čtverců.
Syntaxe, ovládání, možnost
Syntaxe je poměrně jednoduchá a upovídaná. U většiny základních příkazů stačí vypsat název operace v angličtině a za ní pak samotný výraz, přesto je asi ale nejlepší si na počátku projít uvedené příklady, jsou poměrně jednoduché, dají se pěkně kombinovat a ilustrují možnosti Wolfram Alpha. Matematické funkce je možné rozdělit do několika okruhů. Předně je to práce s čísly a elementární výpočetní operace. Aplikace zvládá převody mezi číselnými soustavami, základní aritmetické operace i takové legrace jak je výpočet čísla PI na 10 000 platných číslic.
Zde nabízíme jen jednoduchou ukázku:
(3+7–1/2+4/9) to binary
Výraz se vyhodnotí a převede do binárního zápisu, včetně zápisu binárních čísel v různých normách, a přihodí i převody do dalších běžných číselných soustav. Mimo to poslouží aplikace jako poměrně podrobné matematické tabulky.
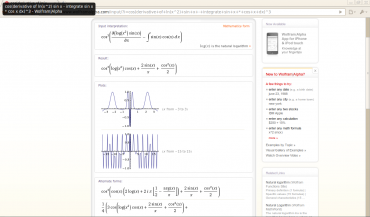
O něco zajímavější jsou integrály a derivace. Ty se postupně zlepšují, tabulkových integrálů již systém umí poměrně hodně a s většinou derivací si také poradí. Příkladem takového výrazu může být například složenina derivací a integrálu:
cos(derivative of ln(x2) sin x – integrate sin x * cos x dx)^3
Kromě výsledku je k dispozici samozřejmě graf, alternativní formy výsledků nebo různé další užitečné aproximace. Není problém řešení symbolické, ani numerické, je možné používat také konstanty.
Mimo to je samozřejmě k dispozici nástroj na řešení rovnic(diferenciální, kvadratických, kubických,…), výrazy se upravují automaticky. Také k nim je sestaven graf, určeny kořeny, průběh funkce atp. Zajímavé jsou také nástroje na tvorbu grafů, výplně ploch či počítání obsahů. Wolfram Alpha si poradí i se základními geometrickými problémy nebo zvládne základy maticového počtu.
Samostatnou kapitolou jsou nástroje pro analýzu a vizualizaci dat. K dispozici je několik možností proložení zadaných bodů. Aplikace pak vygeneruje koeficienty k jednotlivým členům, ovšem bez informace o chybě, takže se hodí spíše pro orientační měření. Jelikož ale systém podporuje i práci s řadami, není příliš velký problém si chyby dopočítat zvlášť, jedná se tedy o zcela zbytečný nedostatek, který může některé uživatele nepříjemně překvapit.
Ze statistických nástrojů jsou k dispozici jednak zmíněné regrese (lineární, kvadratická, kubická, exponenciální,..), ale také různé distribuce nebo základy kombinatoriky. Mimo to je možné si vytvořit graf ze zadaných hodnot a aplikace k němu automaticky opět doplní některé užitečné údaje. Zde je příklad zadání dat a jejich lineární proložení:
linear fit {1.3, 2.2},{2.1, 5.8},{3.7, 10.2},{4.2, 11.8}
Možnosti systému jsou poměrně bohaté. Jako pozitivum je možné uvést, že každý graf či výraz lze zobrazit jako kód pro matematiku, případně čistý text nebo celou stránku vyexportovat do pdf (ač ne příliš hezkého). Celkově se ale jedná o zřejmě nejlepší online CAS, který pro občasné použití nebo mobilní práci bohatě vystačí a nabízí při méně náročných výpočtech i poměrně svižnou odpověď. Na druhou stranu je jasné, že pro složité výpočty nebo ukládání mezivýsledků, celkový export do LaTeX a další činnosti, které od CAS očekáváme, Wolfram Alpha nenabízí a zřejmě jen tak nenabídne. Celkově se ale aplikace velice rychle zlepšuje a jistě stojí přinejmenším za vyzkoušení.