Obsah
1. Tvorba grafů v programovacím jazyku R
2. Zdroj dat pro dnešní demonstrační příklady
3. Korelační diagram (bodový graf)
4. Přidání popisku grafu a popisků os
5. Nastavení limitů (rozsahů) na souřadných osách
6. Matice několika korelačních diagramů
7. Změna stylu vykreslení grafu
8. Přidání textu (popisků) k vykresleným bodům
10. Přikreslení úseček do diagramu
11. Vykreslení dvojice horizontálních úseček do diagramu
12. Nastavení stylu vykreslení úseček
15. Regresní přímka v diagramu
16. Průměr a směrodatná odchylka
17. Zakreslení obou statistických hodnot do diagramu
18. Získání koeficientů z regresního modelu
19. Repositář s demonstračními příklady
1. Tvorba grafů v programovacím jazyku R
Již v předchozím článku jsme se seznámili s principem tvorby jednoduchých sloupcových grafů, popř. grafů, do nichž byl přidán i liniový průběh. Tato problematika je ovšem velmi rozsáhlá, takže se jí budeme zabývat mj. i dnes. V jazyku R lze grafy a popř. i jiné formy grafického výstupu realizovat s využitím několika knihoven, které se od sebe liší tím, zda používají nízkoúrovňový či vysokoúrovňový přístup při popisu grafu, resp. při specifikaci jednotlivých kroků vykreslování. Navíc existuje několik knihoven, které jsou na dané úrovni použitelné. Některé z těchto knihoven jsou zmíněny v následujícím seznamu:
- Nízkoúrovňový přístup
- Funkce ze základní knihovny jazyka R
- Balíček grid
- Vysokoúrovňový přístup
- Balíček lattice
- Balíček ggplot
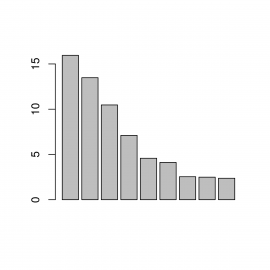
Obrázek 1: Jednoduchý sloupcový graf s hodnotami vyčtenými z datového rámce.
Pro interaktivní grafy (či obecně grafiku) je možné využít například tyto knihovny:
- Balíček rggobi
- Balíček iplots
- Balíček rgl
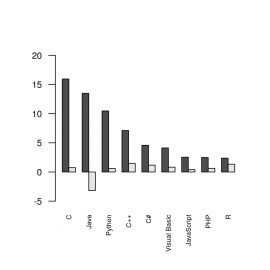
Obrázek 2: Dvě skupiny sloupců na sloupcovém grafu zobrazené vedle sebe.
2. Zdroj dat pro dnešní demonstrační příklady
Grafy, které budou použity v dnešních demonstračních příkladech, budou používat datový rámec, který je součástí základní knihovny programovacího jazyka R. Tento datový rámec je pojmenován mtcars a obsahuje informace o 32 modelech automobilů z roků 1973 a 1974. O každém automobilu je zaznamenáno jedenáct numerických informací:
help(mtcars)
mtcars package:datasets R Documentation
Motor Trend Car Road Tests
Description:
The data was extracted from the 1974 _Motor Trend_ US magazine,
and comprises fuel consumption and 10 aspects of automobile design
and performance for 32 automobiles (1973-74 models).
Usage:
mtcars
Format:
A data frame with 32 observations on 11 variables.
[, 1] mpg Miles/(US) gallon
[, 2] cyl Number of cylinders
[, 3] disp Displacement (cu.in.)
[, 4] hp Gross horsepower
[, 5] drat Rear axle ratio
[, 6] wt Weight (1000 lbs)
[, 7] qsec 1/4 mile time
[, 8] vs V/S
[, 9] am Transmission (0 = automatic, 1 = manual)
[,10] gear Number of forward gears
[,11] carb Number of carburetors
Source:
Henderson and Velleman (1981), Building multiple regression models
interactively. _Biometrics_, *37*, 391-411.
Examples:
require(graphics)
pairs(mtcars, main = "mtcars data")
coplot(mpg ~ disp | as.factor(cyl), data = mtcars,
panel = panel.smooth, rows = 1)
Podívejme se nyní na obsah tohoto datového rámce. Můžeme vidět, že jednotlivé sloupce jsou pojmenovány (což je obvyklé), ovšem pojmenovány jsou i řádky. Samotné jméno modelu automobilu tedy není uloženo v samostatném sloupci (tím lze datový rámec odlišit od běžné databázové tabulky):
print(mtcars)
mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160.0 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160.0 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108.0 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258.0 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360.0 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225.0 105 2.76 3.460 20.22 1 0 3 1
Duster 360 14.3 8 360.0 245 3.21 3.570 15.84 0 0 3 4
Merc 240D 24.4 4 146.7 62 3.69 3.190 20.00 1 0 4 2
Merc 230 22.8 4 140.8 95 3.92 3.150 22.90 1 0 4 2
Merc 280 19.2 6 167.6 123 3.92 3.440 18.30 1 0 4 4
Merc 280C 17.8 6 167.6 123 3.92 3.440 18.90 1 0 4 4
Merc 450SE 16.4 8 275.8 180 3.07 4.070 17.40 0 0 3 3
Merc 450SL 17.3 8 275.8 180 3.07 3.730 17.60 0 0 3 3
Merc 450SLC 15.2 8 275.8 180 3.07 3.780 18.00 0 0 3 3
Cadillac Fleetwood 10.4 8 472.0 205 2.93 5.250 17.98 0 0 3 4
Lincoln Continental 10.4 8 460.0 215 3.00 5.424 17.82 0 0 3 4
Chrysler Imperial 14.7 8 440.0 230 3.23 5.345 17.42 0 0 3 4
Fiat 128 32.4 4 78.7 66 4.08 2.200 19.47 1 1 4 1
Honda Civic 30.4 4 75.7 52 4.93 1.615 18.52 1 1 4 2
Toyota Corolla 33.9 4 71.1 65 4.22 1.835 19.90 1 1 4 1
Toyota Corona 21.5 4 120.1 97 3.70 2.465 20.01 1 0 3 1
Dodge Challenger 15.5 8 318.0 150 2.76 3.520 16.87 0 0 3 2
AMC Javelin 15.2 8 304.0 150 3.15 3.435 17.30 0 0 3 2
Camaro Z28 13.3 8 350.0 245 3.73 3.840 15.41 0 0 3 4
Pontiac Firebird 19.2 8 400.0 175 3.08 3.845 17.05 0 0 3 2
Fiat X1-9 27.3 4 79.0 66 4.08 1.935 18.90 1 1 4 1
Porsche 914-2 26.0 4 120.3 91 4.43 2.140 16.70 0 1 5 2
Lotus Europa 30.4 4 95.1 113 3.77 1.513 16.90 1 1 5 2
Ford Pantera L 15.8 8 351.0 264 4.22 3.170 14.50 0 1 5 4
Ferrari Dino 19.7 6 145.0 175 3.62 2.770 15.50 0 1 5 6
Maserati Bora 15.0 8 301.0 335 3.54 3.570 14.60 0 1 5 8
Volvo 142E 21.4 4 121.0 109 4.11 2.780 18.60 1 1 4 2
3. Korelační diagram (bodový graf)
První typ grafu, se kterým se dnes seznámíme, je korelační diagram, který je ovšem někdy známý i pod jménem bodový graf (scatter plot). Tento graf se vykresluje funkcí plot, které se předají minimálně informace o x-ových a y-ových souřadnicích bodů, jež se mají do grafu vykreslit:
plot(x, y, main, xlab, ylab, xlim, ylim, axes)
Tento graf využijeme pro zobrazení korelace mezi hmotností auta (tisíce liber) a spotřebou uvedenou v jednotkách míle/galon. Pro převod na jednotky používané v našem regionu lze využít tento graf:
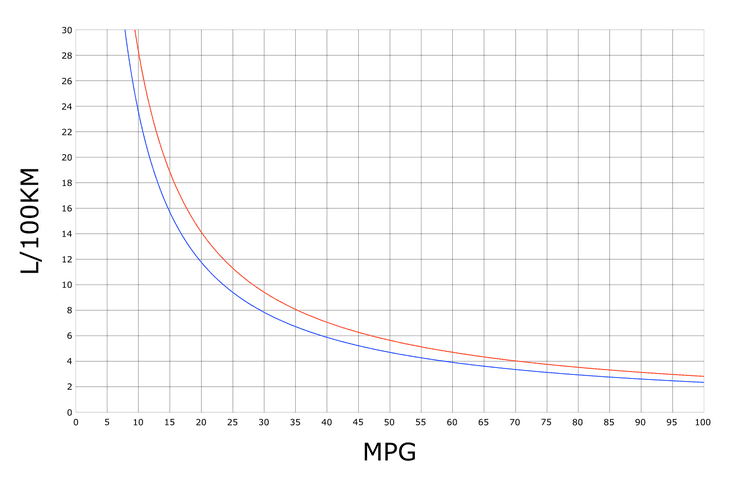
Obrázek 3: Přepočet mezi spotřebou v jednotkách l/100 a mpg.
Zdroj: https://commons.wikimedia.org/wiki/File:Chart_MPG_to_L-100km_v2009–10–08.svg
Nejprve si připomeňme, jakým způsobem se z datového rámce získají jen ty řádky, které nás zajímají. Jeden z možných způsobů:
input <- mtcars[,c('wt','mpg')]
print(input)
wt mpg
Mazda RX4 2.620 21.0
Mazda RX4 Wag 2.875 21.0
Datsun 710 2.320 22.8
Hornet 4 Drive 3.215 21.4
Hornet Sportabout 3.440 18.7
Valiant 3.460 18.1
Duster 360 3.570 14.3
Merc 240D 3.190 24.4
Merc 230 3.150 22.8
Merc 280 3.440 19.2
Merc 280C 3.440 17.8
Merc 450SE 4.070 16.4
Merc 450SL 3.730 17.3
Merc 450SLC 3.780 15.2
Cadillac Fleetwood 5.250 10.4
Lincoln Continental 5.424 10.4
Chrysler Imperial 5.345 14.7
Fiat 128 2.200 32.4
Honda Civic 1.615 30.4
Toyota Corolla 1.835 33.9
Toyota Corona 2.465 21.5
Dodge Challenger 3.520 15.5
AMC Javelin 3.435 15.2
Camaro Z28 3.840 13.3
Pontiac Firebird 3.845 19.2
Fiat X1-9 1.935 27.3
Porsche 914-2 2.140 26.0
Lotus Europa 1.513 30.4
Ford Pantera L 3.170 15.8
Ferrari Dino 2.770 19.7
Maserati Bora 3.570 15.0
Volvo 142E 2.780 21.4
Nyní již můžeme použít nový datový rámec a vybrat z něho hodnoty pro x-ové souřadnice a souřadnice y-ové:
input <- mtcars[,c('wt','mpg')]
plot(x = input$wt,y = input$mpg)
Výsledný diagram by měl vypadat následovně:
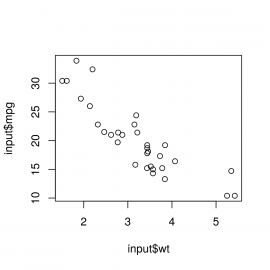
Obrázek 4: Korelační diagram mezi hmotností a spotřebou auta.
4. Přidání popisku grafu a popisků os
Korelační diagram nyní můžeme snadno upravovat specifikací dalších (nepovinných) parametrů. S využitím parametrů xlab, ylab a main můžeme do grafu přidat jeho titulek a popisky jednotlivých os:
input <- mtcars[,c('wt','mpg')]
plot(x = input$wt, y = input$mpg,
xlab = "Weight",
ylab = "Mileage",
main = "Weight vs Mileage"
)
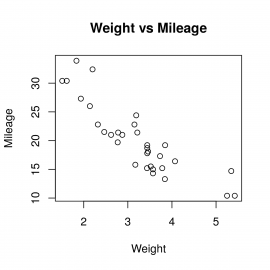
Obrázek 5: Graf s přidaným titulkem i popiskami obou os.
5. Nastavení limitů (rozsahů) na souřadných osách
Poměrně často se setkáme s tím, že ze všech bodů (tedy dvojic souřadnic [x,y]) budeme chtít vybrat pouze body ležící v nějaké oblasti. V korelačním diagramu pochopitelně můžeme nastavovat limity (nebo rozsahy) na obou souřadných osách. K tomuto účelu slouží nepovinné parametry nazvané xlim a ylim, kterým se předává dvouprvkový vektor s minimální a maximální hodnotou na dané ose:
input <- mtcars[,c('wt','mpg')]
plot(x = input$wt,y = input$mpg,
xlab = "Weight",
ylab = "Mileage",
main = "Weight vs Mileage",
xlim = c(2.5,5),
ylim = c(15,30)
)
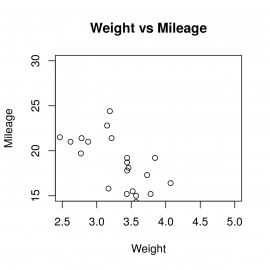
Obrázek 6: Výřez hodnot z předchozího grafu.
6. Matice několika korelačních diagramů
V úvodních kapitolách jsme si ukázali datový rámec, který obsahuje celkem jedenáct různých numerických hodnot o každém modelu automobilu. Mezi některými hodnotami typicky existují různé korelace. A právě zde nastává problém – jakým způsobem zobrazit nebo vůbec nalézt korelace mezi několika hodnotami? Ke zkoumání korelací může posloužit skupina grafů zobrazená funkcí pairs, která zobrazí nikoli jeden korelační diagram, ale matici několika diagramů:
help(pairs)
pairs package:graphics R Documentation
Scatterplot Matrices
Description:
A matrix of scatterplots is produced.
Usage:
pairs(x, ...)
## S3 method for class 'formula'
pairs(formula, data = NULL, ..., subset,
na.action = stats::na.pass)
## Default S3 method:
pairs(x, labels, panel = points, ...,
horInd = 1:nc, verInd = 1:nc,
lower.panel = panel, upper.panel = panel,
diag.panel = NULL, text.panel = textPanel,
label.pos = 0.5 + has.diag/3, line.main = 3,
cex.labels = NULL, font.labels = 1,
row1attop = TRUE, gap = 1, log = "")
...
...
...
Details:
The ijth scatterplot contains ‘x[,i]’ plotted against ‘x[,j]’.
The scatterplot can be customised by setting panel functions to
appear as something completely different. The off-diagonal panel
functions are passed the appropriate columns of ‘x’ as ‘x’ and
‘y’: the diagonal panel function (if any) is passed a single
column, and the ‘text.panel’ function is passed a single ‘(x, y)’
location and the column name. Setting some of these panel
functions to ‘NULL’ is equivalent to _not_ drawing anything there.
Podívejme se nyní na demonstrační příklady. V prvním příkladu je zobrazena matice s korelacemi mezi sloupcem wt a mpg a současně i diagram s opačnou korelací (tento diagram odpovídá grafu původnímu, pouze je zrcadlen). Diagonální diagramy obsahují jméno hodnoty, takže lze velmi snadno dohledat, jakou závislost každý z poddiagramů zobrazuje:
input <- mtcars
pairs(~wt+mpg, data = input,
main = "Scatterplot Matrix", cex.axis=0.5)
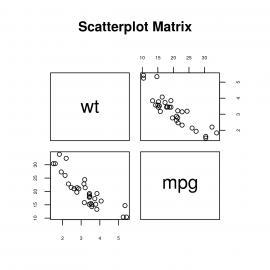
Obrázek 7: Korelace mezi hodnotami ve dvou sloupcích.
Ovšem velmi snadno můžeme přidat i další sloupec, takže se nám zobrazí šestice různých korelačních diagramů:
input <- mtcars
pairs(~wt+mpg+disp, data = input,
main = "Scatterplot Matrix", cex.axis=0.5)
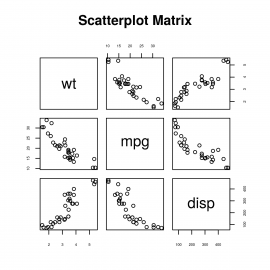
Obrázek 8: Korelace mezi hodnotami ve třech sloupcích.
Nic nám nebrání v přidání čtvrtého sloupce – počet válců (zde jsou hodnoty nejméně náhodné):
input <- mtcars
pairs(~wt+mpg+disp+cyl, data = input,
main = "Scatterplot Matrix", cex.axis=0.5)
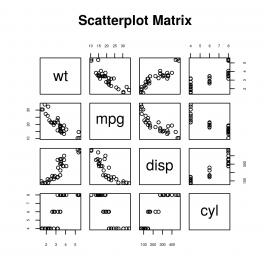
Obrázek 9: Korelace mezi hodnotami ve čtyřech sloupcích.
Popř. můžeme zobrazit všechny možné kombinace korelací, což ovšem s ohledem na omezené rozlišení výsledných obrázků není vůbec praktické (muselo by se použít mnohem větší rozlišení):
input <- mtcars
pairs(input, data = input,
main = "Scatterplot Matrix", cex.axis=0.5)

Obrázek 10: Korelace mezi hodnotami ve všech jedenácti sloupcích.
7. Změna stylu vykreslení grafu
Vraťme se nyní k funkci plot. Pokud se podíváme na původní grafy, zjistíme, že by je bylo možné vizuálně vylepšit. Původní korelační diagram:
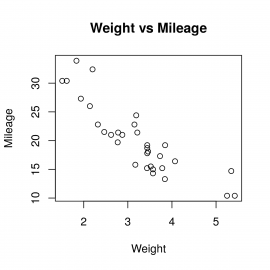
Obrázek 11: Původní korelační diagram.
změníme na:
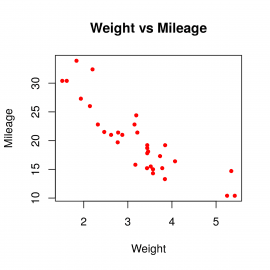
Obrázek 12: Korelační diagram s upravenými styly.
Musíme tedy změnit tvar bodů a jejich barvu. K tomu slouží nepovinné parametry pch a col:
input <- mtcars
plot(x = input$wt,y = input$mpg,
xlab = "Weight",
ylab = "Mileage",
main = "Weight vs Mileage",
pch=20,
col="red"
)
Tvar bodů (resp. číslo tvaru) si vyberte z následujícího seznamu:
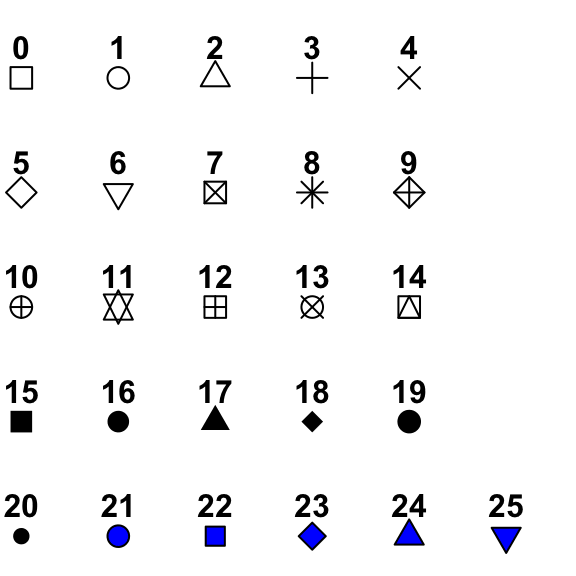
8. Přidání textu (popisků) k vykresleným bodům
Do korelačního diagramu je možné přidat i text, resp. přesněji řečeno návěští k jednotlivým vykresleným bodům. K tomuto účelu slouží funkce nazvaná text, kterou lze zavolat po vykreslení grafu. Této funkci se předají x-ové souřadnice, y-ové souřadnice a vlastní textové popisky, což jsou v našem případě jména jednotlivých řádků v datovém rámci:
text(input$wt, input$mpg, rownames(input), cex=0.5)
^ ^ ^
x y vlastní text
Úplný zdrojový kód tohoto demonstračního příkladu vypadá následovně:
input <- mtcars plot(x = input$wt,y = input$mpg, xlab = "Weight", ylab = "Mileage", main = "Weight vs Mileage", pch=20, col="red" ) text(input$wt, input$mpg, rownames(input), cex=0.5)
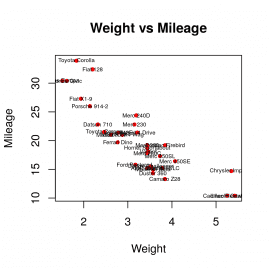
Obrázek 13: Přidání popisků do korelačního diagramu.
9. Posun popisků v diagramu
Na předchozím obrázku je patrné, že se popisky překrývají s body, které mají popisovat. Tento nedostatek je možné do určité míry napravit tak, že text popisků posuneme (samotné body samozřejmě posunovat nesmíme, protože by nekorespondovaly s osami). Posun popisků lze snadno provést, protože jeden sloupec datového rámce je považován za vektor a k prvkům vektoru se může připočítat skalární hodnota (resp. se opět jedná o vektor, který je „natažen“ do správné délky):
input <- mtcars input$wt input$mpg
Příklad vypíše původní vektory:
[1] 2.620 2.875 2.320 3.215 3.440 3.460 3.570 3.190 3.150 3.440 3.440 4.070 [13] 3.730 3.780 5.250 5.424 5.345 2.200 1.615 1.835 2.465 3.520 3.435 3.840 [25] 3.845 1.935 2.140 1.513 3.170 2.770 3.570 2.780 [1] 21.0 21.0 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 17.8 16.4 17.3 15.2 10.4 [16] 10.4 14.7 32.4 30.4 33.9 21.5 15.5 15.2 13.3 19.2 27.3 26.0 30.4 15.8 19.7 [31] 15.0 21.4
Posun vektorů:
input <- mtcars input$wt + 2 input$mpg + 0.7
Výsledky:
[1] 4.620 4.875 4.320 5.215 5.440 5.460 5.570 5.190 5.150 5.440 5.440 6.070 [13] 5.730 5.780 7.250 7.424 7.345 4.200 3.615 3.835 4.465 5.520 5.435 5.840 [25] 5.845 3.935 4.140 3.513 5.170 4.770 5.570 4.780 [1] 21.7 21.7 23.5 22.1 19.4 18.8 15.0 25.1 23.5 19.9 18.5 17.1 18.0 15.9 11.1 [16] 11.1 15.4 33.1 31.1 34.6 22.2 16.2 15.9 14.0 19.9 28.0 26.7 31.1 16.5 20.4 [31] 15.7 22.1
Stejnou operaci můžeme provést při volání funkce text, což je patrné ze zdrojového kódu následujícího demonstračního příkladu:
input <- mtcars plot(x = input$wt,y = input$mpg, xlab = "Weight", ylab = "Mileage", main = "Weight vs Mileage", pch=20, col="red", xlim = c(2.5,4.3), ylim = c(15,26), ) text(input$wt+0, input$mpg+0.7, rownames(input), cex=0.4)
Nyní by měly být popisky posunuty a současně by se měl ukázat jen výřez ze všech hodnot:
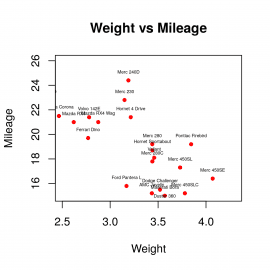
Obrázek 14: Posun popisků a zobrazení výrazu z grafu.
10. Přikreslení úseček do diagramu
Mnohdy je zapotřebí do diagramu (prakticky libovolného typu) přikreslit úsečky, které například budou ukazovat lineární trend, nějaké vymezené hodnoty apod. Příkladem může být graf, který jsme si ukázali v první části tohoto seriálu a který ukazuje teoretický poměr korelace mezi popularitou programovacích jazyků na serverech StackOverflow a na GitHubu:
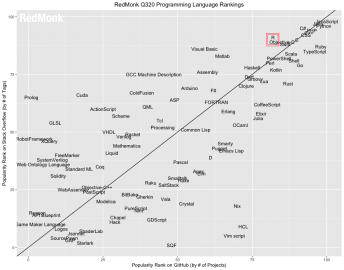
Obrázek 15: Jazyk R na RedMonku (viz zvýrazněnou část) + teoretická korelace mezi popularitou programovacích jazyků na serverech StackOverflow a na GitHubu.
Zdroj: https://redmonk.com/
Úsečky je možné do grafu zakreslit funkcí pojmenovanou abline, kterou opět nalezneme ve standardní knihovně programovacího jazyka R:
help(abline)
abline package:graphics R Documentation
Add Straight Lines to a Plot
Description:
This function adds one or more straight lines through the current
plot.
Usage:
abline(a = NULL, b = NULL, h = NULL, v = NULL, reg = NULL,
coef = NULL, untf = FALSE, ...)
Arguments:
a, b: the intercept and slope, single values.
untf: logical asking whether to _untransform_. See ‘Details’.
h: the y-value(s) for horizontal line(s).
v: the x-value(s) for vertical line(s).
coef: a vector of length two giving the intercept and slope.
reg: an object with a ‘coef’ method. See ‘Details’.
...: graphical parameters such as ‘col’, ‘lty’ and ‘lwd’ (possibly
as vectors: see ‘Details’) and ‘xpd’ and the line
characteristics ‘lend’, ‘ljoin’ and ‘lmitre’.
Povšimněte si, že úsečku je možné zadat několika způsoby:
- posunem a sklonem
- y-ovou souřadnicí v případě horizontální úsečky
- x-ovou souřadnicí v případě úsečky vertikální
- vektorem obsahujícím posun a sklon
- výsledkem výpočtu lineární regrese
- atd.
11. Vykreslení dvojice horizontálních úseček do diagramu
Podívejme se nyní na způsob vykreslení dvojice horizontálních úseček do diagramu. V tomto případě nám postačuje zadat pouze posun a žádné další hodnoty (popř. pouze parametr h):
input <- mtcars plot(x = input$wt,y = input$mpg, xlab = "Weight", ylab = "Mileage", main = "Weight vs Mileage", pch=20, col="red" ) text(input$wt+0, input$mpg+0.7, rownames(input), cex=0.2) abline(20,0) abline(25,0)
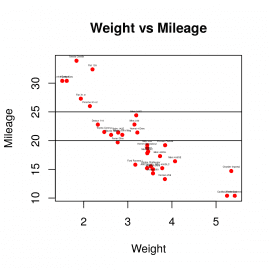
Obrázek 16: Dvojice horizontálních úseček dokreslená do diagramu.
Alternativní způsob zápisu:
input <- mtcars plot(x = input$wt,y = input$mpg, xlab = "Weight", ylab = "Mileage", main = "Weight vs Mileage", pch=20, col="red" ) text(input$wt+0, input$mpg+0.7, rownames(input), cex=0.2) abline(a=20, b=0) abline(a=25, b=0)
Popř. je možné specifikovat vzdálenost horizontálních úseček od osy x:
input <- mtcars plot(x = input$wt,y = input$mpg, xlab = "Weight", ylab = "Mileage", main = "Weight vs Mileage", pch=20, col="red" ) text(input$wt+0, input$mpg+0.7, rownames(input), cex=0.2) abline(h=20) abline(h=25)
12. Nastavení stylu vykreslení úseček
Styl vykreslení úseček lze ovlivnit několika parametry, zejména pak parametry col, lty a lwd:
| # | Parametr | Stručný popis |
|---|---|---|
| 1 | col | barva úsečky |
| 2 | lty | styl čáry zapsaný celým číslem 1 až 6 |
| 3 | lwd | šířka vykreslení úsečky |
Podívejme se na příklad, v němž se vykreslí dvě úsečky s různým stylem:
input <- mtcars plot(x = input$wt,y = input$mpg, xlab = "Weight", ylab = "Mileage", main = "Weight vs Mileage", pch=20, col="red" ) text(input$wt+0, input$mpg+0.7, rownames(input), cex=0.2) abline(20, 0, col='blue', lty=2, lwd=1) abline(25, 0, col='darkgreen', lty=2, lwd=1)
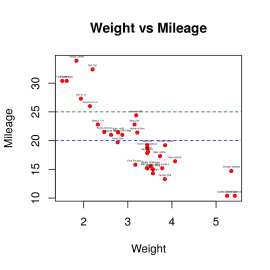
Obrázek 17: Změna stylu vykreslení úseček.
13. Šest stylů úseček
Samotný styl úseček (což je celé číslo v rozsahu 1 až 6), resp. přesněji řečeno všech šest stylů, si ukážeme takto:
plot(0, xlim=c(1,7), ylim=c(1,6)) abline(h=1, lwd=1, lty=1, col="black") abline(h=2, lwd=1, lty=2, col="blue") abline(h=3, lwd=1, lty=3, col="cyan") abline(h=4, lwd=1, lty=4, col="green") abline(h=5, lwd=1, lty=5, col="orange") abline(h=6, lwd=1, lty=6, col="red")
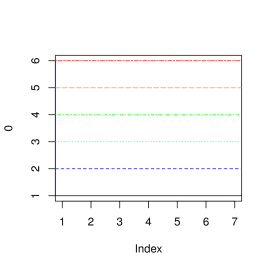
Obrázek 18: Šest stylů úseček.
14. Lineární regrese
Programovací jazyk R obsahuje již ve své základní knihovně velmi užitečnou funkci pro výpočet lineární regrese, tj. pro proložení souboru bodů v grafu přímkou, a to tak, aby odchylky bodů od této přímky byly (v součtu, resp. součtu čtverců) co nejmenší. Předpokládá se přitom, že body představují naměřenou veličinu s lineárním průběhem. Pro výpočet lineární regrese se používá funkce nazvaná lm:
help(lm)
lm package:stats R Documentation
Fitting Linear Models
Description:
‘lm’ is used to fit linear models. It can be used to carry out
regression, single stratum analysis of variance and analysis of
covariance (although ‘aov’ may provide a more convenient interface
for these).
Usage:
lm(formula, data, subset, weights, na.action,
method = "qr", model = TRUE, x = FALSE, y = FALSE, qr = TRUE,
singular.ok = TRUE, contrasts = NULL, offset, ...)
...
...
...
Jednoduchý příklad pro výpočet regresní přímky pro soustavu bodů, které skutečně na přímce leží:
x <- c(1,2,3,4) y <- c(2,4,6,8) + 10 regression <- lm(y~x) regression
Výsledek nám říká, že sklon přímky (směrnice) je roven 2 a posun 10:
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x
10 2
Můžeme se například pokusit získat regresní přímku, která by odpovídala korelaci mezi hodnotami ve sloupcích mpg (spotřeba) a wt (váha):
input <- mtcars regression <- lm(input$mpg~input$wt) regression
Výsledkem by měly být koeficienty vypočtené přímky (opět posun a sklon/směrnice):
Call:
lm(formula = input$mpg ~ input$wt)
Coefficients:
(Intercept) input$wt
37.285 -5.344
15. Regresní přímka v diagramu
Přidání regresní přímky do korelačního diagramu je snadné, což je ostatně patrné i ze zdrojového kódu následujícího demonstračního příkladu. Povšimněte si přitom, že výsledek výpočtu regrese nemusíme rozkládat na posun a směrnici, protože ve funkci abline lze použít parametr reg:
input <- mtcars plot(x = input$wt,y = input$mpg, xlab = "Weight", ylab = "Mileage", main = "Weight vs Mileage", pch=20, col="red" ) text(input$wt+0, input$mpg+0.7, rownames(input), cex=0.2) abline(20,0,col='blue', lty=2, lwd=1) abline(25,0,col='darkgreen', lty=2, lwd=1) regression <- lm(input$mpg~input$wt) abline(reg=regression, col='lightblue', lwd=2)
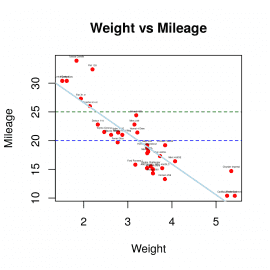
Obrázek 19: Regresní přímka v diagramu.
16. Průměr a směrodatná odchylka
Do našeho korelačního diagramu přidáme několik úseček, které mají praktický význam. Jedna z úseček bude reprezentovat průměr hodnot (mean), druhé dvě pak směrodatnou odchylku (standard deviation). Průměr se vypočte velmi snadno funkcí nazvanou přímočaře mean:
help(mean)
mean package:base R Documentation
Arithmetic Mean
Description:
Generic function for the (trimmed) arithmetic mean.
Usage:
mean(x, ...)
## Default S3 method:
mean(x, trim = 0, na.rm = FALSE, ...)
Příklad výpočtu:
input <- mtcars mean(input$mpg) [1] 20.09062
Směrodatná odchylka se vypočte funkcí nazvanou sd:
help(sd)
sd package:stats R Documentation
Standard Deviation
Description:
This function computes the standard deviation of the values in
‘x’. If ‘na.rm’ is ‘TRUE’ then missing values are removed before
computation proceeds.
Usage:
sd(x, na.rm = FALSE)
Příklad výpočtu:
input <- mtcars sd(input$mpg) [1] 6.026948
Více nás však budou v grafu zajímat odchylky od průměru, tedy:
input <- mtcars m <- mean(input$mpg) s <- sd(input$mpg) m - s m + s
S výsledky:
[1] 14.06368 [1] 26.11757
17. Zakreslení obou statistických hodnot do diagramu
Přidání obou statistických hodnot do diagramu je již snadné. Průměr bude reprezentován světle červenou vodorovnou úsečkou, odchylky od průměru pak světle modrou úsečkou. V diagramu ponecháme i regresní přímku:
input <- mtcars plot(x = input$wt,y = input$mpg, xlab = "Weight", ylab = "Mileage", main = "Weight vs Mileage", pch=20, col="red" ) text(input$wt+0, input$mpg+0.7, rownames(input), cex = 0.2) abline(h = mean(input$mpg), col = '#ff8080', lwd = 1, lty = 2) abline(h = mean(input$mpg) + sd(input$mpg), col = 'steelblue', lwd = 1, lty = 2) abline(h = mean(input$mpg) - sd(input$mpg), col = 'steelblue', lwd = 1, lty = 2) regression <- lm(input$mpg~input$wt) abline(reg=regression, col='lightblue', lwd=2)
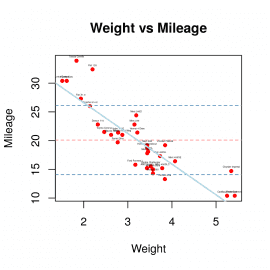
Obrázek 20: Průměr o odchylky od průměru v korelačním diagramu.
18. Získání koeficientů z regresního modelu
Na závěr si ve stručnosti ukažme, jak je možné z výsledku regresního modelu získat oba koeficienty přímky, tedy jak její sklon, tak i posun:
input <- mtcars
regression <- lm(input$mpg~input$wt)
a <- coefficients(regression)[1] #intercept
b <- coefficients(regression)[2] #slope
regression
print("intercept")
a
print("slope")
b
Po spuštění skriptu se nejprve zobrazí výsledek výpočtu regrese a následně i oba koeficienty:
Call:
lm(formula = input$mpg ~ input$wt)
Coefficients:
(Intercept) input$wt
37.285 -5.344
[1] "intercept"
(Intercept)
37.28513
[1] "slope"
input$wt
-5.344472
Příklad pro vykreslení korelačního diagramu tedy můžeme upravit takovým způsobem, že úsečku zadáme koeficienty a a b, které byly získány právě z regresního modelu:
input <- mtcars plot(x = input$wt,y = input$mpg, xlab = "Weight", ylab = "Mileage", main = "Weight vs Mileage", pch=20, col="red" ) text(input$wt+0, input$mpg+0.7, rownames(input), cex = 0.2) abline(h = mean(input$mpg), col = '#ff8080', lwd = 1, lty = 2) abline(h = mean(input$mpg) + sd(input$mpg), col = 'steelblue', lwd = 1, lty = 2) abline(h = mean(input$mpg) - sd(input$mpg), col = 'steelblue', lwd = 1, lty = 2) regression <- lm(input$mpg~input$wt) a <- coefficients(regression)[1] #intercept b <- coefficients(regression)[2] #slope abline(a=a, b=b, col="steelblue", lwd=2)
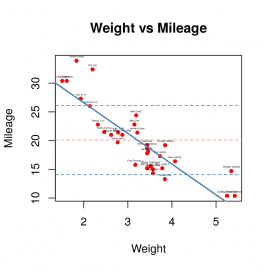
Obrázek 21: Totožný diagram, jaký byl vypočten i předchozím demonstračním příkladem.
19. Repositář s demonstračními příklady
Zdrojové kódy všech dnes použitých demonstračních příkladů byly uloženy do nového Git repositáře, který je dostupný na adrese https://github.com/tisnik/r-examples V případě, že z nějakého důvodu nebudete chtít klonovat celý repositář (ten je ovšem – alespoň prozatím – velmi malý, dnes má stále jen jednotky kilobajtů), můžete namísto toho použít odkazy na jednotlivé demonstrační příklady, které naleznete v následující tabulce:
20. Odkazy na Internetu
- The R Project for Statistical Computing
https://www.r-project.org/ - An Introduction to R
https://cran.r-project.org/doc/manuals/r-release/R-intro.pdf - R (programming language)
https://en.wikipedia.org/wiki/R_(programming_language) - The R Programming Language
https://www.tiobe.com/tiobe-index/r/ - Grid
https://www.stat.auckland.ac.nz/~paul/grid/grid.html - Lattice: Multivariate Data Visualization with R
http://lmdvr.r-forge.r-project.org/figures/figures.html - R Markdown
https://rmarkdown.rstudio.com/ - R Markdown: The Definitive Guide
https://bookdown.org/yihui/rmarkdown/ - R Markdown Cheat Sheet
https://rstudio.com/wp-content/uploads/2016/03/rmarkdown-cheatsheet-2.0.pdf - Introduction to R Markdown
https://rmarkdown.rstudio.com/articles_intro.html - R Cheat Sheets
https://blog.sergiouri.be/2016/07/r-cheat-sheets.html - R Cheat Sheet
https://s3.amazonaws.com/quandl-static-content/Documents/Quandl±+R+Cheat+Sheet.pdf - Base R Cheat Sheet
https://rstudio.com/wp-content/uploads/2016/06/r-cheat-sheet.pdf - PYPL PopularitY of Programming Language
https://pypl.github.io/PYPL.html - Tiobe index
https://www.tiobe.com/tiobe-index/ - Stack Overflow: Most Loved, Dreaded & Wanted Programming Languages In 2020
https://fossbytes.com/stack-overflow-most-loved-dreaded-wanted-programming-languages-in-2020/ - How to Install and Use R on Ubuntu
https://itsfoss.com/install-r-ubuntu/ - R programming for beginners – Why you should use R
https://www.youtube.com/watch?v=9kYUGMg_14s - GOTO 2012 • The R Language The Good The Bad & The Ugly
https://www.youtube.com/watch?v=6S9r_YbqHy8 - R vs Python – What should I learn in 2020? | R and Python Comparison
https://www.youtube.com/watch?v=eRP_J2yLjSU - R Programming 101
https://www.youtube.com/c/rprogramming101 - Seriál Tvorba grafů pomocí programu „R“
https://www.root.cz/serialy/tvorba-grafu-pomoci-programu-r/ - Tvorba grafů pomocí programu „R“: úvod
https://www.root.cz/clanky/tvorba-grafu-pomoci-programu-r-1/ - Tvorba grafů pomocí programu „R“: pokročilé funkce
https://www.root.cz/clanky/tvorba-grafu-pomoci-programu-r-pokrocile-funkce/ - Tvorba grafů pomocí programu „R“: vkládání textu, čeština
https://www.root.cz/clanky/grafy-pomoci-programu-r-vkladani-textu-cestina/ - Cesta erka: Krok nultý – instalace & nastavení – prostředí, projekty, package
https://www.jla-data.net/r4su/r4su-environment-setup/ - Cesta erka: Krok první – operace a struktury – proměnné, rovnítka a dolary
https://www.jla-data.net/r4su/r4su-data-structures/ - Cesta erka: Krok druhý – načtení externích dat – csvčka, excely a databáze
https://www.jla-data.net/r4su/r4su-read-data/ - Cesta erka: Krok třetí – manipulace s daty – dplyr, slovesa a pajpy
https://www.jla-data.net/r4su/r4su-manipulate-data/ - Cesta erka: Krok čtvrtý – podání výsledků – ggplot, geomy a estetiky
https://www.jla-data.net/r4su/r4su-report-results/ - Cesta erka: Krok pátý – case study – případ piva v Praze
https://www.jla-data.net/r4su/r4su-case-study-beer/ - V indexu popularity programovacích jazyků TIOBE překvapilo R, Go, Perl, Scratch a Rust
https://www.root.cz/zpravicky/v-indexu-popularity-programovacich-jazyku-tiobe-prekvapilo-r-go-perl-scratch-a-rust/ - Is R Programming SURGING in Popularity in 2020?
https://www.youtube.com/watch?v=Duwn-vImyXE - Using the R programming language in Jupyter Notebook
https://docs.anaconda.com/anaconda/navigator/tutorials/r-lang/ - Using R on Jupyter Notebook
https://dzone.com/articles/using-r-on-jupyternbspnotebook - Graphics, ggplot2
http://r4stats.com/examples/graphics-ggplot2/ - A Practice Data Set
https://r4stats.wordpress.com/examples/mydata/ - Shiny – galerie projektů
https://shiny.rstudio.com/gallery/ - Seriál Programovací jazyk Julia
https://www.root.cz/serialy/programovaci-jazyk-julia/ - Julia (front page)
http://julialang.org/ - Julia – repositář na GitHubu
https://github.com/JuliaLang/julia - Julia (programming language)
https://en.wikipedia.org/wiki/Julia_%28programming_language%29 - IJulia
https://github.com/JuliaLang/IJulia.jl - Introducing Julia
https://en.wikibooks.org/wiki/Introducing_Julia - Julia: the REPL
https://en.wikibooks.org/wiki/Introducing_Julia/The_REPL - Introducing Julia/Metaprogramming
https://en.wikibooks.org/wiki/Introducing_Julia/Metaprogramming - Month of Julia
https://github.com/DataWookie/MonthOfJulia - Learn X in Y minutes (where X=Julia)
https://learnxinyminutes.com/docs/julia/ - New Julia language seeks to be the C for scientists
http://www.infoworld.com/article/2616709/application-development/new-julia-language-seeks-to-be-the-c-for-scientists.html - Julia: A Fast Dynamic Language for Technical Computing
http://karpinski.org/publications/2012/julia-a-fast-dynamic-language - The LLVM Compiler Infrastructure
http://llvm.org/ - Julia: benchmarks
http://julialang.org/benchmarks/ - R Vector
https://www.datamentor.io/r-programming/vector/ - .R File Extension
https://fileinfo.com/extension/r - Lineární regrese
https://cs.wikipedia.org/wiki/Line%C3%A1rn%C3%AD_regrese - lm (funkce)
https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/lm - quit (funkce)
https://www.rdocumentation.org/packages/base/versions/3.6.2/topics/quit - c (funkce)
https://www.rdocumentation.org/packages/base/versions/3.6.2/topics/c - help (funkce)
https://www.rdocumentation.org/packages/utils/versions/3.6.2/topics/help - Shiny: Introduction to interactive documents
https://shiny.rstudio.com/articles/interactive-docs.html - R Release History 1997–2013
http://timelyportfolio.github.io/rCharts_timeline_r/ - R: atomic vectors
https://renenyffenegger.ch/notes/development/languages/R/data-structures/vector/ - 11 Best R Programming IDE and editors
https://www.dunebook.com/best-r-programming-ide/ - CRAN – The Comprehensive R Archive Network
https://cran.r-project.org/ - R – Arrays
https://www.tutorialspoint.com/r/r_arrays.htm - Array vs Matrix in R Programming
https://www.geeksforgeeks.org/array-vs-matrix-in-r-programming/?ref=rp - Online R Language IDE
https://www.jdoodle.com/execute-r-online/ - Execute R Online (R v3.4.1)
https://www.tutorialspoint.com/execute_r_online.php - Snippets: Run any R code you like. There are over twelve thousand R packages preloaded
https://rdrr.io/snippets/ - R Package Documentation
https://rdrr.io/ - Data Reshaping in R – Popular Functions to Organise Data
https://techvidvan.com/tutorials/data-reshaping-in-r/ - What is an R Data Frame?
https://magoosh.com/data-science/what-is-an-r-data-frame/ - What's a data frame?
https://campus.datacamp.com/courses/free-introduction-to-r/chapter-5-data-frames?ex=1 - data.frame
https://www.rdocumentation.org/packages/base/versions/3.6.2/topics/data.frame - as.data.frame
https://www.rdocumentation.org/packages/base/versions/3.6.2/topics/as.data.frame - table
https://www.rdocumentation.org/packages/base/versions/3.6.2/topics/table - Python Pandas – DataFrame
https://www.tutorialspoint.com/python_pandas/python_pandas_dataframe.htm - The Pandas DataFrame: Make Working With Data Delightful
https://realpython.com/pandas-dataframe/ - Python | Pandas DataFrame
https://www.geeksforgeeks.org/python-pandas-dataframe/ - R – Factors
https://www.tutorialspoint.com/r/r_factors.htm - R – Scatterplots
https://www.tutorialspoint.com/r/r_scatterplots.htm - Quick guide to line types (lty) in R
https://www.benjaminbell.co.uk/2018/02/quick-guide-to-line-types-lty-in-r.html






































