Obsah
1. Dokončení popisu knihovny lattice – zbylé typy diagramů
2. Nastavení uspořádání mřížky, do které se grafy vykreslují
3. Další ukázky změny uspořádání grafů v mřížce
4. Seskupování a podmínky v 3D grafech
5. Zobrazení hodnot v polích, popř. průběhů funkcí z=f(x,y)
6. Zvýraznění výšek barvou (výšková mapa)
7. Zvýšení přesnosti zobrazení
8. Modifikace barvové palety výškové mapy
9. Přidání kontur (vrstevnic) do výškové mapy
10. Vrstevnice a barvová paleta výškové mapy
12. Modifikace grafu s konturami
14. Zobrazení nastavení diagramů
15. Drátový (3D) diagram a jeho varianty
17. Ukázky základních možností knihovny ggplot2
18. Obsah následující části seriálu
19. Repositář s demonstračními příklady
1. Dokončení popisu knihovny lattice – zbylé typy diagramů
V dnešním článku o programovacím jazyku R navážeme na téma, kterým jsme se začali zabývat minule. Jedná se o knihovnu Lattice, která byla vyvinuta na základě starší knihovny nazvané Trellis Graphics. Ta byla určena pro systém S a S-PLUS. Za vývojem Trellis Graphics stál především R. A. Becker a W. S. Cleveland. Koncepty, které byly v knihovně Trellis Graphics implementovány, byly použity a ukázány i v Clevelandově knize nazvané Visualizing Data, která byla poprvé vydána již v roce 1993. Ovšem je nutné zdůraznit, že Lattice není pouhým přepisem Trellis Graphics; při přechodu ze systému S na R totiž došlo k mnoha vylepšením a taktéž k úpravám API.
Již minule jsme si popsali některé (jednodušší) typy grafů, včetně způsobu jejich umístění do mřížek (grid). Zbylé důležité grafy poskytované knihovnou Lattice budou popsány v článku dnešním. V tabulce pod tímto odstavcem jsou uvedeny odkazy na kapitoly, v nichž jsou jednotlivé typy grafů popsány a kde jsou jejich možnosti prezentovány na demonstračních příkladech:
| # | Jméno funkce pro vykreslení | Stručný popis |
|---|---|---|
| 1 | barchart | sloupcový graf |
| 2 | histogram | klasický histogram |
| 3 | densityplot | zobrazení distribuce dat přes spojitý interval (zobecnění histogramů) |
| 4 | bwplot | takzvané krabicové grafy (hodnota + rozptyl atd.) |
| 5 | dotplot | bodový graf |
| 6 | qqmath | grafy kvantilu proti matematickým rozložením |
| 7 | stripplot | korelační diagram, ovšem pouze jednodimenzionální |
| 8 | xyplot | bodový vícedimenzionální graf |
| 9 | porovnání dvou rozložení | |
| 10 | cloud | bodový graf v trojrozměrném prostoru |
| 11 | contourplot | zobrazení kontur (vrstevnice, popř. izobary na mapě atd.) |
| 12 | wireframe | zobrazení průběhu, popř. naměřených hodnot ve formě 3D povrchu (drátový model) |
| 13 | levelplot | zakódování výšky formou barevné informace |
2. Nastavení uspořádání mřížky, do které se grafy vykreslují
V předchozím článku jsme si ukázali, že grafy je možné uspořádat do mřížek. Jako příklad si můžeme uvést graf typu xyplot, přesněji řečeno větší množství grafů ukazujících spotřebu auta v závislosti na jeho hmotnosti a navíc na počtu rychlostních stupňů:
library(lattice)
input <- mtcars[,c('wt','mpg','hp','gear','cyl')]
gear.f <- factor(input$gear,
levels = c(3,4,5),
labels = c("3 gears","4 gears","5 gears"))
cyl.f <- factor(input$cyl,
levels=c(4,6,8),
labels=c("4 cyl","6 cyl","8 cyl"))
xyplot(wt~mpg | gear.f,
data=input,
xlab = "Miles/(US) gallons",
ylab = "Weight (1000lbs)")
Výsledek bude vypadat následovně:
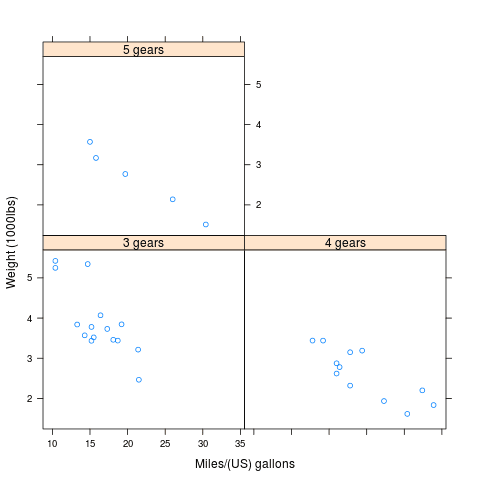
Obrázek 1: Tři grafy typu xyplot umístěné do mřížky.
[1] 4 gears 4 gears 4 gears 3 gears 3 gears 3 gears 3 gears 4 gears 4 gears [10] 4 gears 4 gears 3 gears 3 gears 3 gears 3 gears 3 gears 3 gears 4 gears [19] 4 gears 4 gears 3 gears 3 gears 3 gears 3 gears 3 gears 4 gears 5 gears [28] 5 gears 5 gears 5 gears 5 gears 4 gears Levels: 3 gears 4 gears 5 gears [1] 6 cyl 6 cyl 4 cyl 6 cyl 8 cyl 6 cyl 8 cyl 4 cyl 4 cyl 6 cyl 6 cyl 8 cyl [13] 8 cyl 8 cyl 8 cyl 8 cyl 8 cyl 4 cyl 4 cyl 4 cyl 4 cyl 8 cyl 8 cyl 8 cyl [25] 8 cyl 4 cyl 4 cyl 4 cyl 8 cyl 6 cyl 8 cyl 4 cyl Levels: 4 cyl 6 cyl 8 cyl
Způsob umístění grafů do mřížky je ovšem možné modifikovat, a to pojmenovaným parametrem layout, v němž určíme rozměr mřížky (počet sloupců × počet řádků):
library(lattice)
input <- mtcars[,c('wt','mpg','hp','gear','cyl')]
gear.f <- factor(input$gear,
levels = c(3,4,5),
labels = c("3 gears","4 gears","5 gears"))
cyl.f <- factor(input$cyl,
levels=c(4,6,8),
labels=c("4 cyl","6 cyl","8 cyl"))
xyplot(wt~mpg | gear.f,
data=input,
xlab = "Miles/(US) gallons",
ylab = "Weight (1000lbs)",
layout = (c(1,3)))
Nyní bude výsledek vypadat odlišně:
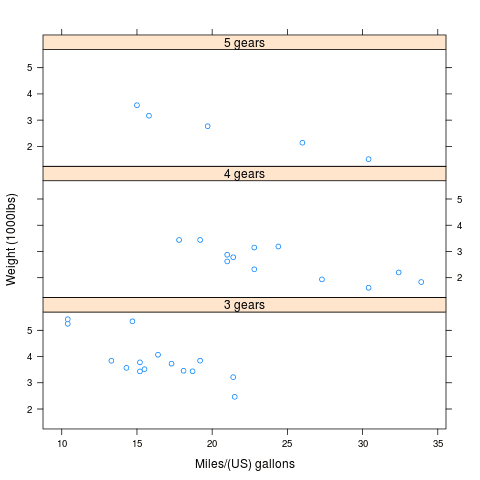
Obrázek 2: Grafy umístěné v mřížce pod sebou.
Do grafů pochopitelně můžeme přidat regresní přímku, aproximaci bodů křivkou atd. (což nemá žádný vliv na umístění grafů do mřížky):
library(lattice)
input <- mtcars[,c('wt','mpg','hp','gear','cyl')]
gear.f <- factor(input$gear,
levels = c(3,4,5),
labels = c("3 gears","4 gears","5 gears"))
cyl.f <- factor(input$cyl,
levels = c(4,6,8),
labels = c("4 cyl","6 cyl","8 cyl"))
xyplot(wt~mpg | gear.f,
data=input,
type = c("p", "r"),
xlab = "Miles/(US) gallons",
ylab = "Weight (1000lbs)",
layout = (c(1,3)))
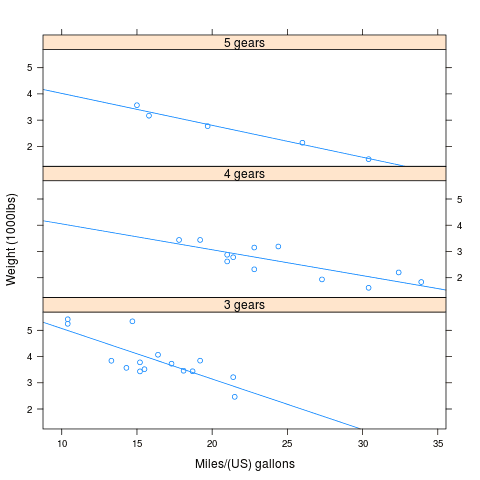
Obrázek 3: Grafy (včetně regresní přímky) umístěné v mřížce pod sebou.
3. Další ukázky změny uspořádání grafů v mřížce
Podobným způsobem je možné uspořádat i jiné typy grafů, popř. grafy s odlišnými vstupními daty. Opět si připomeňme demonstrační příklad z předchozího článku, v němž je použit datový set nazvaný iris:
library(lattice)
data("iris")
head(iris)
input <- iris[,c('Sepal.Length','Sepal.Width','Petal.Length','Petal.Width','Species')]
xyplot(Sepal.Length ~ Petal.Length | Species,
group = Species,
data = input,
type = c("p", "smooth"),
scales = "free")
S výsledkem:
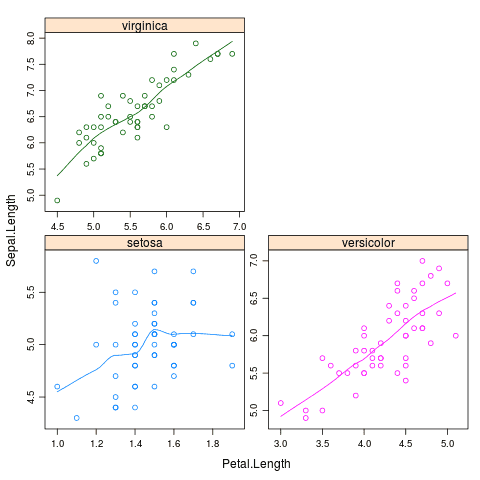
Obrázek 4: Tři grafy typu xyplot umístěné do mřížky 2×2 prvky.
Tyto grafy je možné v případě potřeby umístit pod sebe do jediného obrázku:
library(lattice)
data("iris")
head(iris)
input <- iris[,c('Sepal.Length','Sepal.Width','Petal.Length','Petal.Width','Species')]
xyplot(Sepal.Length ~ Petal.Length | Species,
group = Species,
data = input,
type = c("p", "smooth"),
layout = (c(1,3)))
S tímto výsledkem:
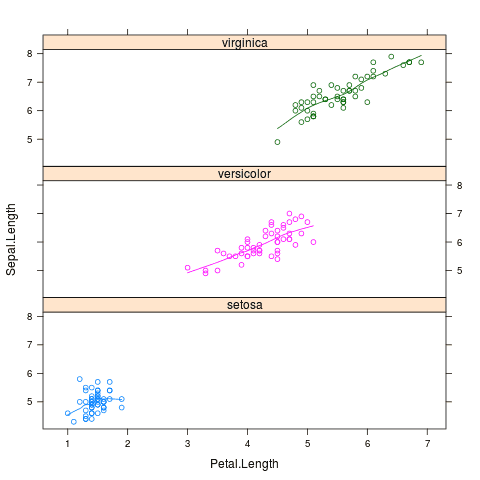
Obrázek 5: Tři grafy typu xyplot umístěné do mřížky 3×1 prvek.
4. Seskupování a podmínky v 3D grafech
Připomeňme si, že s využitím knihovny Lattice je možné vykreslovat 3D grafy, v nichž jsou vyneseny body popsané třemi souřadnicemi. Vstupní data pro takové grafy jsou typicky představována trojicí vektorů nebo datovým rámcem s příslušnými (třemi) sloupci:
library(lattice)
data("iris")
head(iris)
input <- iris[,c('Sepal.Length','Sepal.Width','Petal.Length','Petal.Width')]
cloud(Sepal.Length~Sepal.Width*Petal.Length,
data = input,
auto.key=TRUE)
Vytvořený výsledek:
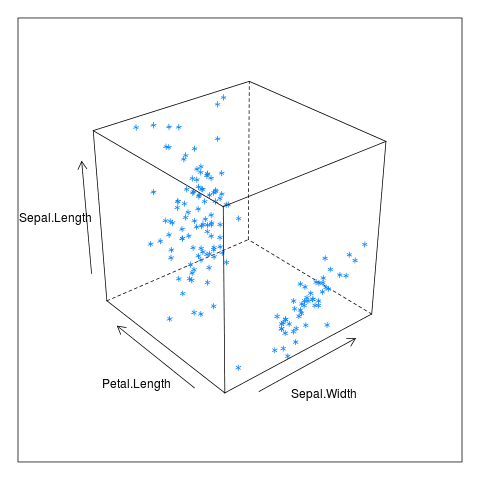
Obrázek 6: Trojrozměrný graf s vynesenými body.
Tyto grafy je možné (podobně jako prakticky i všechny ostatní grafy) rozdělit podle čtvrté hodnoty, resp. přesněji vektoru či faktoru s hodnotami. Zápis této čtvrté hodnoty je proveden za znakem |:
library(lattice)
data("iris")
head(iris)
input <- iris[,c('Sepal.Length','Sepal.Width','Petal.Length','Petal.Width','Species')]
cloud(Sepal.Length~Sepal.Width*Petal.Length | Species,
data = input,
auto.key = TRUE,
layout = (c(3,1)))
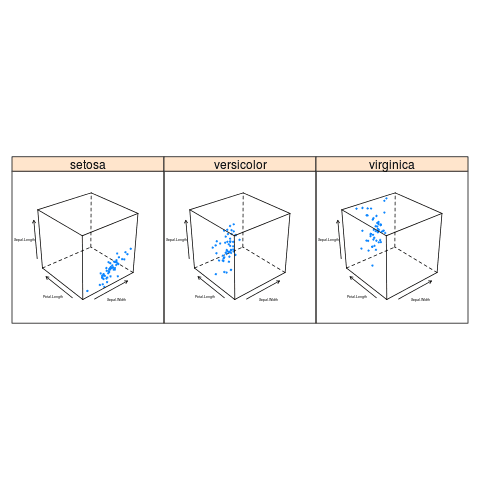
Obrázek 7: Umístění tří grafů vedle sebe (viz volba layout).
Tento typ grafů většinou vyžaduje změnu velikosti písma použitého při popisu souřadných os. Pro tento účel se používají parametry xlab, ylab a zlab, kterým se předá seznam obsahující jeden pojmenovaný prvek cex s relativní hodnotou písma:
library(lattice)
data("iris")
head(iris)
input <- iris[,c('Sepal.Length','Sepal.Width','Petal.Length','Petal.Width','Species')]
cloud(Sepal.Length~Sepal.Width*Petal.Length | Species,
data = input,
auto.key = TRUE,
layout = (c(3,1)),
xlab = list(cex = 0.3),
ylab = list(cex = 0.3),
zlab = list(cex = 0.3))
S výsledkem:
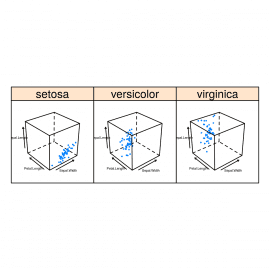
Obrázek 8: Modifikace velikosti popisků na souřadných osách.
I v tomto typu grafu je možné sdružit hodnoty podle třetí, resp. čtvrté hodnoty. K tomuto účelu použijeme parametr nazvaný group, podobně, jako jsme to dělali u jiných typů grafů:
library(lattice)
data("iris")
head(iris)
input <- iris[,c('Sepal.Length','Sepal.Width','Petal.Length','Petal.Width','Species')]
cloud(Sepal.Length ~ Sepal.Length*Petal.Width,
data = input,
group = Species,
auto.key = TRUE)
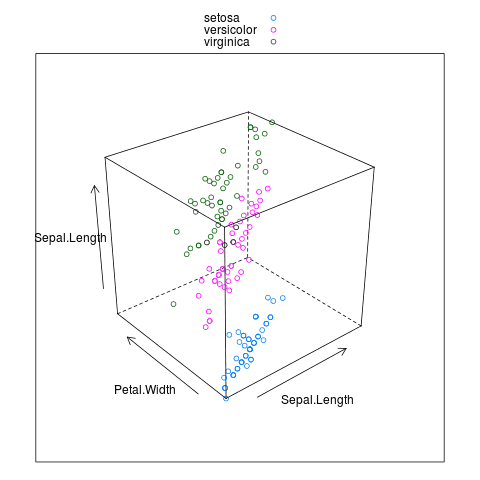
Obrázek 9: Sdružení hodnot v grafu na základě hodnot uložených ve vektoru Species.
Pro úplnost si ještě ukažme kombinaci obou předchozích možností. Navíc parametrem pch změníme styl vykreslování bodů:
library(lattice)
data("iris")
head(iris)
input <- iris[,c('Sepal.Length','Sepal.Width','Petal.Length','Petal.Width','Species')]
cloud(Sepal.Length ~ Sepal.Width*Petal.Width,
data = input,
group = Species,
auto.key = TRUE,
pch = 19,
xlab = list(cex=0.6),
ylab = list(cex=0.6),
zlab = list(cex=0.6))
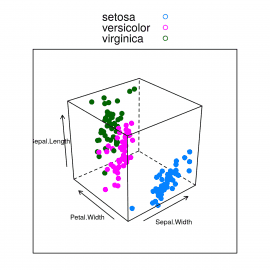
Obrázek 10: Změna stylu vykreslení bodů v grafu typu cloud.
5. Zobrazení hodnot v polích, popř. průběhů funkcí z=f(x,y)
Poměrně často se setkáme s nutností nějakým způsobem vizualizovat průběh funkce z=f(x,y), popř. vizualizovat hodnoty uložené v dvojrozměrné matici (může se jednat o naměřené hodnoty atd.). K vizualizaci lze použít relativně velké množství technik, přičemž jednou známou technikou je zvýraznění výšek barvou (vznikne výšková mapa), použití kontur (vrstevnic), popř. vykreslení drátového modelu v případě, že se jedná o spojitou funkci. V následujících kapitolách se seznámíme se všemi třemi zmíněnými možnostmi – každý typ vizualizace je přitom v knihovně Lattice představován odlišným typem grafu.
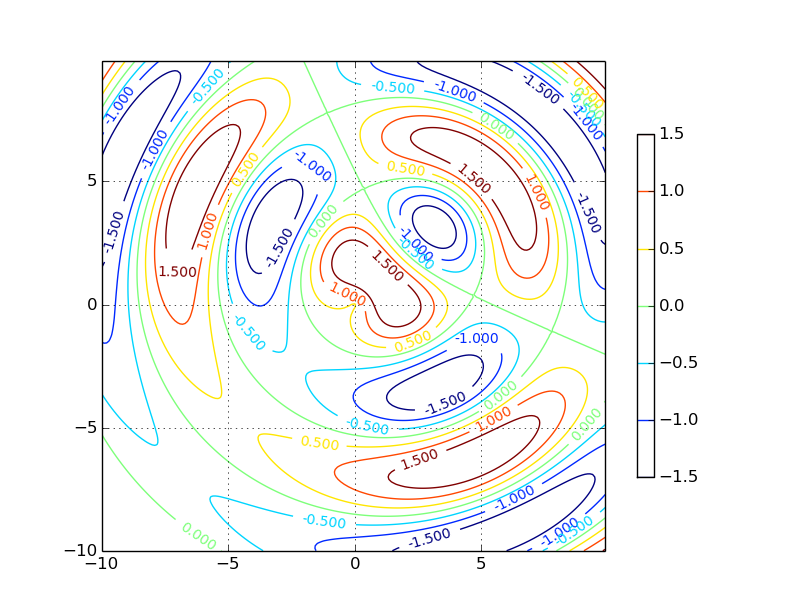
Obrázek 11: Jeden typ grafu podporovaný knihovnou Matplotlib – Funkce typu z=f(x,y) zobrazená formou vrstevnic.
Podobné typy grafů nalezneme i v knihovně Matplotlib používané v jazyku Python a mnohdy kombinovanou s knihovnou Numpy. Pro porovnání s dále uvedenými grafy jsou v této kapitole zobrazeny dvě vizualizace provedené právě Matplotlibem.
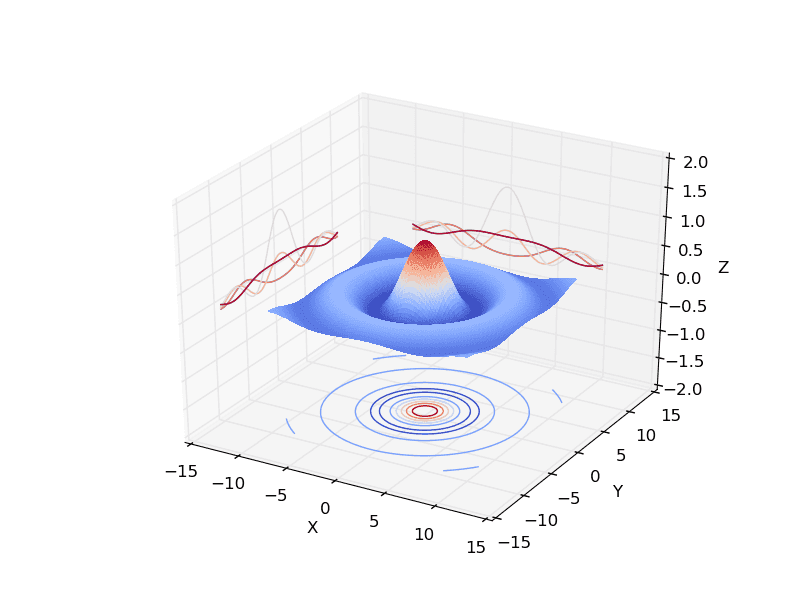
Obrázek 12: Podporována je i relativně široká skupina 3D grafů.
6. Zvýraznění výšek barvou (výšková mapa)
Pro vykreslení výškové mapy (viděné ze směru osy z) se zvýrazněním výšek různými barvami se používá graf pojmenovaný levelplot. Ve zcela nejjednodušším příkladu si necháme zobrazit data uložená ve vektoru volcano (Maunga Whau, resp. Mt Eden):
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14]
[1,] 100 100 101 101 101 101 101 100 100 100 101 101 102 102
[2,] 101 101 102 102 102 102 102 101 101 101 102 102 103 103
[3,] 102 102 103 103 103 103 103 102 102 102 103 103 104 104
[4,] 103 103 104 104 104 104 104 103 103 103 103 104 104 104
[5,] 104 104 105 105 105 105 105 104 104 103 104 104 105 105
[6,] 105 105 105 106 106 106 106 105 105 104 104 105 105 106
[,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25] [,26]
[1,] 102 102 103 104 103 102 101 101 102 103 104 104
[2,] 103 103 104 105 104 103 102 102 103 105 106 106
[3,] 104 104 105 106 105 104 104 105 106 107 108 110
[4,] 105 105 106 107 106 106 106 107 108 110 111 114
[5,] 105 106 107 108 108 108 109 110 112 114 115 118
[6,] 106 107 109 110 110 112 113 115 116 118 119 121
[,27] [,28] [,29] [,30] [,31] [,32] [,33] [,34] [,35] [,36] [,37] [,38]
[1,] 105 107 107 107 108 108 110 110 110 110 110 110
[2,] 107 109 110 110 110 110 111 112 113 114 116 115
[3,] 111 113 114 115 114 115 116 118 119 119 121 121
[4,] 117 118 117 119 120 121 122 124 125 126 127 127
[5,] 121 122 121 123 128 131 129 130 131 131 132 132
[6,] 124 126 126 129 134 137 137 136 136 135 136 136
[,39] [,40] [,41] [,42] [,43] [,44] [,45] [,46] [,47] [,48] [,49] [,50]
[1,] 110 110 108 108 108 107 107 108 108 108 108 108
[2,] 114 112 110 110 110 109 108 109 109 109 109 108
[3,] 120 118 116 114 112 111 110 110 110 110 109 109
[4,] 126 124 122 120 117 116 113 111 110 110 110 109
[5,] 131 130 128 126 122 119 115 114 112 110 110 110
[6,] 136 135 133 129 126 122 118 116 115 113 111 110
[,51] [,52] [,53] [,54] [,55] [,56] [,57] [,58] [,59] [,60] [,61]
[1,] 107 107 107 107 106 106 105 105 104 104 103
[2,] 108 108 108 107 107 106 106 105 105 104 104
[3,] 109 109 108 108 107 107 106 106 105 105 104
[4,] 109 109 109 108 108 107 107 106 106 105 105
[5,] 110 110 109 109 108 107 107 107 106 106 105
[6,] 110 110 110 109 108 108 108 107 107 106 106
Vykreslení se provede jediným příkazem:
library("lattice")
head(volcano)
levelplot(volcano)
S tímto výsledkem:
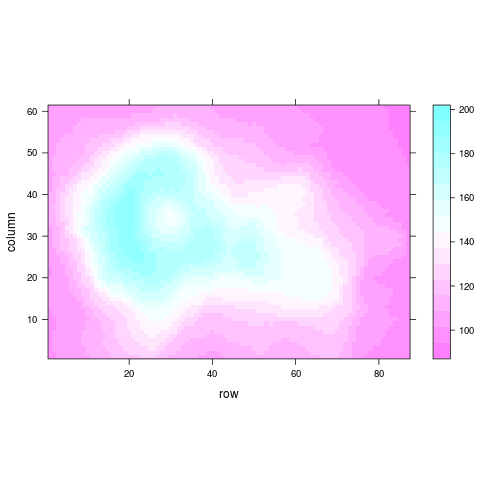
Obrázek 13: Zobrazení hodnot uložených v proměnné volcano.
Zobrazit však můžeme i průběh složitější funkce:
library("lattice")
x <- seq(1, 2*pi, length.out=20)
y <- seq(1, 2*pi, length.out=20)
r1 <- as.vector(sqrt(outer(x^2, y^2, "+")))
r2 <- as.vector(sqrt(outer((x-3)^2, (y-3)^2, "+")))
grid <- expand.grid(x=x, y=y)
grid$z <- sin(r1) + sin(r2)
levelplot(z ~ x*y,
data=grid,
xlab="X",
main="")
Tento příklad pracuje následovně:
- Vytvoří se dvojice vektorů x a y
- Funkcí outer se vytvoří matice s kombinacemi vektorů x a y se specifikovaným výpočtem
- Výsledek této funkce použijeme pro naplnění pomocných proměnných r1 a r2
- Funkcí expand.grid se vytvoří datový rámec s dvojicí sloupců naplněných obsahem vektorů x a y
- Do datového rámce doplníme třetí sloupec se z-ovými hodnotami
Příklad matice vytvořené funkcí:
outer(seq(1,10), seq(1,10))
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [1,] 1 2 3 4 5 6 7 8 9 10 [2,] 2 4 6 8 10 12 14 16 18 20 [3,] 3 6 9 12 15 18 21 24 27 30 [4,] 4 8 12 16 20 24 28 32 36 40 [5,] 5 10 15 20 25 30 35 40 45 50 [6,] 6 12 18 24 30 36 42 48 54 60 [7,] 7 14 21 28 35 42 49 56 63 70 [8,] 8 16 24 32 40 48 56 64 72 80 [9,] 9 18 27 36 45 54 63 72 81 90 [10,] 10 20 30 40 50 60 70 80 90 100
Příklad matice vytvořené funkcí:
outer(seq(1,10), seq(1,10), "+")
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [1,] 2 3 4 5 6 7 8 9 10 11 [2,] 3 4 5 6 7 8 9 10 11 12 [3,] 4 5 6 7 8 9 10 11 12 13 [4,] 5 6 7 8 9 10 11 12 13 14 [5,] 6 7 8 9 10 11 12 13 14 15 [6,] 7 8 9 10 11 12 13 14 15 16 [7,] 8 9 10 11 12 13 14 15 16 17 [8,] 9 10 11 12 13 14 15 16 17 18 [9,] 10 11 12 13 14 15 16 17 18 19 [10,] 11 12 13 14 15 16 17 18 19 20
Datový rámec vypadá následovně:
x y z 1 1.000000 1.000000 1.295837688 2 1.278062 1.000000 1.480223667 3 1.556125 1.000000 1.586134959 4 1.834187 1.000000 1.604315197 5 2.112250 1.000000 1.535943853 6 2.390312 1.000000 1.390926079 7 2.668374 1.000000 1.185456798 8 2.946437 1.000000 0.939077730 9 3.224499 1.000000 0.671729601 10 3.502561 1.000000 0.401445589 11 3.780624 1.000000 0.143114910 12 4.058686 1.000000 -0.091738191 ... ... ... 394 4.614811 6.283185 0.503842514 395 4.892873 6.283185 0.390274092 396 5.170936 6.283185 0.246646275 397 5.448998 6.283185 0.078826471 398 5.727061 6.283185 -0.105383335 399 6.005123 6.283185 -0.296588296 400 6.283185 6.283185 -0.484313825
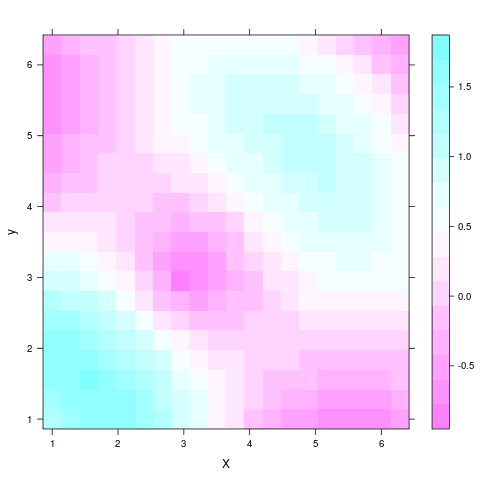
Obrázek 14: Výsledek běhu předchozího demonstračního příkladu.
7. Zvýšení přesnosti zobrazení
V demonstračním příkladu uvedeného v předchozí kapitole je vytvořen datový rámec s pouhými 400 řádky, přičemž z-ové hodnoty jsou uloženy v pravidelné mřížce o „rozlišení“ 20×20 bodů. Rozlišení mřížky můžeme zvýšit, a to typicky tak, že zvětšíme počet prvků ve vektorech x a y. Výsledkem bude, že výšková mapa bude sestrojena na základě mřížky 200×200 (40000) hodnot:
library("lattice")
x <- seq(1, 2*pi, length.out=200)
y <- seq(1, 2*pi, length.out=200)
r1 <- as.vector(sqrt(outer(x^2, y^2, "+")))
r2 <- as.vector(sqrt(outer((x-3)^2, (y-3)^2, "+")))
grid <- expand.grid(x=x, y=y)
grid$z <- sin(r1) + sin(r2)
levelplot(z ~ x*y,
data=grid,
xlab="X",
main="")
Obrázek 15: Nyní je výšková mapa vytvořena na základě mřížky 200×200 hodnot.
8. Modifikace barvové palety výškové mapy
Barvy vykreslení je možné v případě potřeby modifikovat u všech typů grafů, ovšem především u výškové mapy se setkáme s použitím plnohodnotné barvové palety. Ta je specifikována pojmenovaným parametrem col.regions přičemž je k dispozici několik standardních barvových palet. V následujících demonstračních příkladech si je ukážeme.
Barvová paleta terrain:
library("lattice")
x <- seq(1, 2*pi, length.out=200)
y <- seq(1, 2*pi, length.out=200)
r1 <- as.vector(sqrt(outer(x^2, y^2, "+")))
r2 <- as.vector(sqrt(outer((x-3)^2, (y-3)^2, "+")))
grid <- expand.grid(x=x, y=y)
grid$z <- sin(r1) + sin(r2)
levelplot(z ~ x*y,
data=grid,
xlab="",
ylab="",
main="",
col.regions = terrain.colors(100))
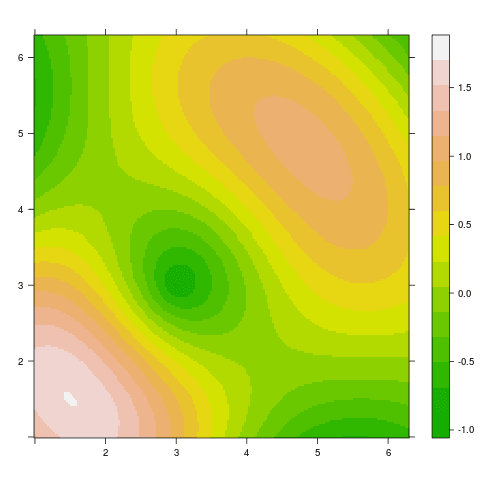
Obrázek 16: Použití barvové palety terrain.
Barvová paleta rainbow:
library("lattice")
x <- seq(1, 2*pi, length.out=200)
y <- seq(1, 2*pi, length.out=200)
r1 <- as.vector(sqrt(outer(x^2, y^2, "+")))
r2 <- as.vector(sqrt(outer((x-3)^2, (y-3)^2, "+")))
grid <- expand.grid(x=x, y=y)
grid$z <- sin(r1) + sin(r2)
levelplot(z ~ x*y,
data=grid,
xlab="",
ylab="",
main="",
col.regions = rainbow(100))
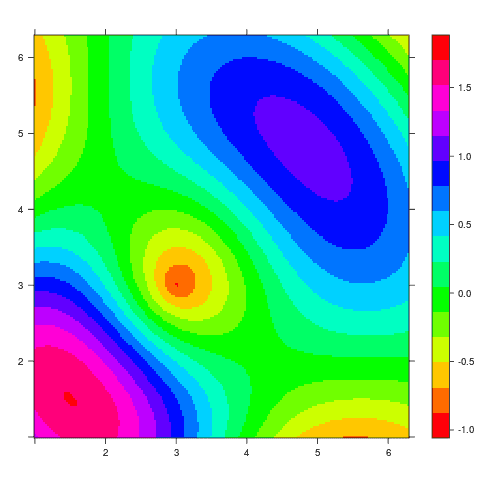
Obrázek 17: Použití barvové palety rainbow.
Barvová paleta heat:
library("lattice")
x <- seq(1, 2*pi, length.out=200)
y <- seq(1, 2*pi, length.out=200)
r1 <- as.vector(sqrt(outer(x^2, y^2, "+")))
r2 <- as.vector(sqrt(outer((x-3)^2, (y-3)^2, "+")))
grid <- expand.grid(x=x, y=y)
grid$z <- sin(r1) + sin(r2)
levelplot(z ~ x*y,
data=grid,
xlab="",
ylab="",
main="",
col.regions = heat.colors(100))
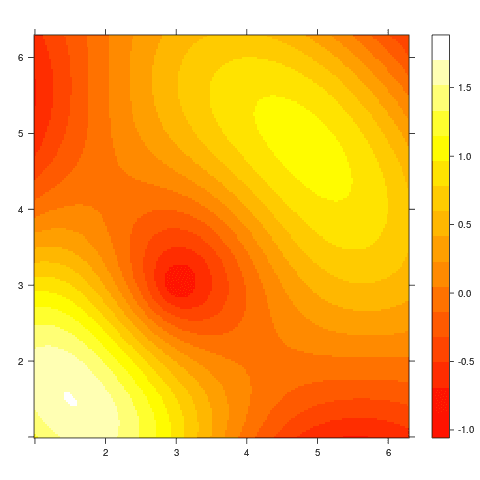
Obrázek 18: Použití barvové palety heat.
Barvová paleta topo:
library("lattice")
x <- seq(1, 2*pi, length.out=200)
y <- seq(1, 2*pi, length.out=200)
r1 <- as.vector(sqrt(outer(x^2, y^2, "+")))
r2 <- as.vector(sqrt(outer((x-3)^2, (y-3)^2, "+")))
grid <- expand.grid(x=x, y=y)
grid$z <- sin(r1) + sin(r2)
levelplot(z ~ x*y,
data=grid,
xlab="",
ylab="",
main="",
col.regions = topo.colors(100))
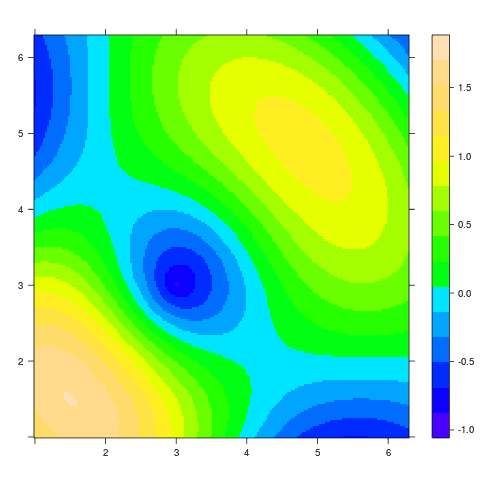
Obrázek 19: Použití barvové palety topo.
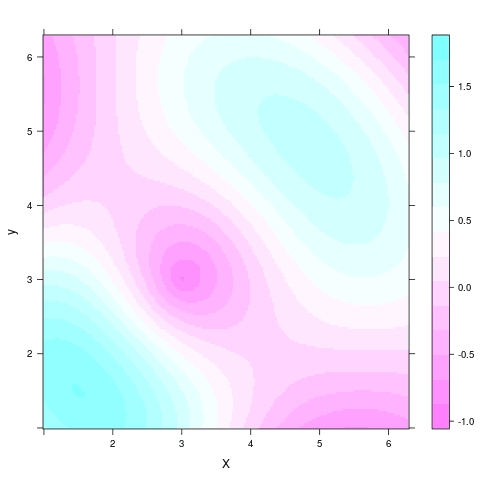
9. Přidání kontur (vrstevnic) do výškové mapy
Do výškové mapy je možné pro zvýraznění oblastí se stejnou či podobnou hodnotou přidat i kontury neboli vrstevnice. Úprava grafu je z pohledu programátora triviální – přidá se pojmenovaný parametr contour nastavený na hodnotu TRUE:
library("lattice")
x <- seq(1.0, 2*pi, length.out=200)
y <- seq(1.0, 2*pi, length.out=200)
r1 <- as.vector(sqrt(outer(x^2, y^2, "+")))
r2 <- as.vector(sqrt(outer((x-3)^2, (y-3)^2, "+")))
grid <- expand.grid(x=x, y=y)
grid$z <- sin(r1) + sin(r2)
levelplot(z ~ x*y,
data=grid,
xlab="",
ylab="",
main="",
contour=TRUE,
col.regions = terrain.colors(20000))
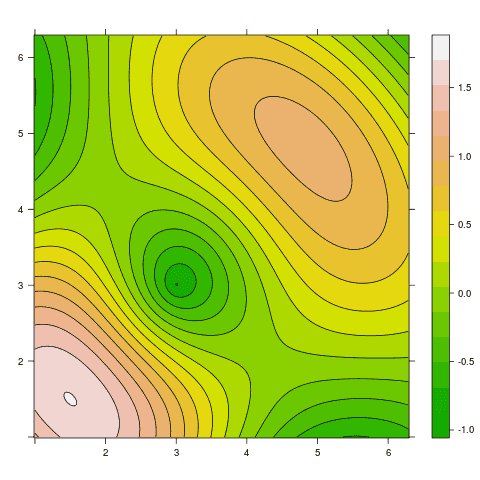
Obrázek 20: Zvýraznění kontur (vrstevnic) ve výškové mapě.
10. Vrstevnice a barvová paleta výškové mapy
Pochopitelně nám nic nebrání i při vykreslení vrstevnic současně vybrat i barvovou paletu pro reprezentaci výšek:
library("lattice")
x <- seq(1.0, 2*pi, length.out=200)
y <- seq(1.0, 2*pi, length.out=200)
r1 <- as.vector(sqrt(outer(x^2, y^2, "+")))
r2 <- as.vector(sqrt(outer((x-3)^2, (y-3)^2, "+")))
grid <- expand.grid(x=x, y=y)
grid$z <- sin(r1) + sin(r2)
levelplot(z ~ x*y,
data=grid,
xlab="",
ylab="",
main="",
contour=TRUE,
col.regions = topo.colors(200))
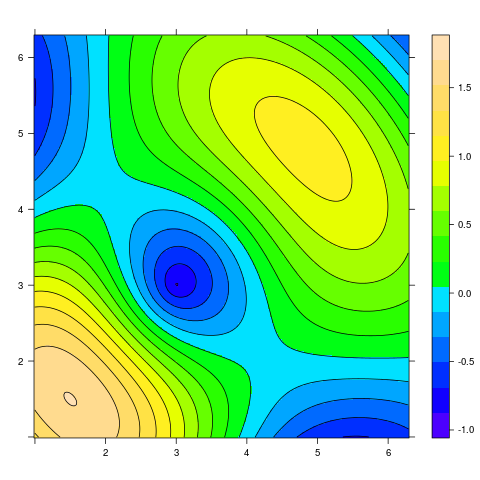
Obrázek 21: Vykreslení vrstevnic a současně i změna barvové palety (topo).
Změna barvové palety na heat:
library("lattice")
x <- seq(1.0, 2*pi, length.out=200)
y <- seq(1.0, 2*pi, length.out=200)
r1 <- as.vector(sqrt(outer(x^2, y^2, "+")))
r2 <- as.vector(sqrt(outer((x-3)^2, (y-3)^2, "+")))
grid <- expand.grid(x=x, y=y)
grid$z <- sin(r1) + sin(r2)
levelplot(z ~ x*y,
data=grid,
xlab="",
ylab="",
main="",
contour=TRUE,
col.regions = heat.colors(200))
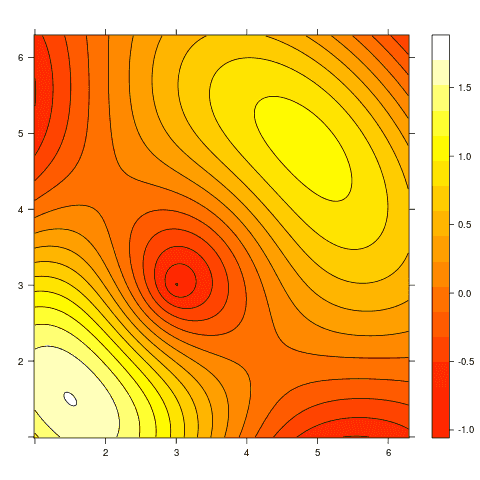
Obrázek 22: Vykreslení vrstevnic a současně i změna barvové palety (heat).
11. Skutečný graf s konturami
Knihovna Lattice obsahuje i další typ grafu nazvaný contourplot. Tento typ grafu vykresluje pouze vrstevnice, nikoli již výšky zakódované do různých barev. Podívejme se, jak tento graf může vypadat, když použijeme stejný zdroj dat, jako v předchozích příkladech (funkce typu z=f(x,y)):
library("lattice")
x <- seq(1.0, 2*pi, length.out=200)
y <- seq(1.0, 2*pi, length.out=200)
r1 <- as.vector(sqrt(outer(x^2, y^2, "+")))
r2 <- as.vector(sqrt(outer((x-3)^2, (y-3)^2, "+")))
grid <- expand.grid(x=x, y=y)
grid$z <- sin(r1) + sin(r2)
contourplot(z ~ x * y,
grid,
col.regions = topo.colors(20),
at = c(-Inf, seq(-0.8, 0.8, by = 0.2), Inf))
Vidíme, že se skutečně spojily ty části plochy, které mají stejnou výšku (a existuje mezi nimi spojení s touto výškou):
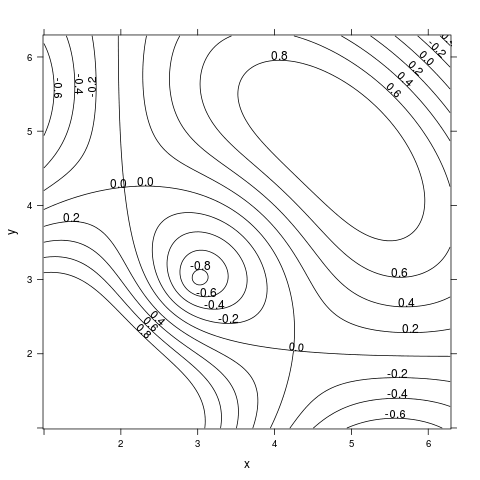
Obrázek 23: Graf s konturami (vrstevnicemi).
12. Modifikace grafu s konturami
Jedna z možných modifikací grafu s konturami (vrstevnicemi) spočívá v tom, že specifikujeme maximální a minimální hodnoty, pro které se mají vrstevnice vykreslit a taktéž krok (rozdíl výšek) mezi vrstevnicemi. Zvolme tedy rozsah od –2,0 do 2,0 s krokem 0,1:
library("lattice")
x <- seq(1.0, 2*pi, length.out=200)
y <- seq(1.0, 2*pi, length.out=200)
r1 <- as.vector(sqrt(outer(x^2, y^2, "+")))
r2 <- as.vector(sqrt(outer((x-3)^2, (y-3)^2, "+")))
grid <- expand.grid(x=x, y=y)
grid$z <- sin(r1) + sin(r2)
contourplot(z ~ x * y, grid, col.regions = topo.colors(20),
at = c(-Inf, seq(-2.0, 2.0, by = 0.1), Inf))
Výsledkem je graf s více než dvojnásobným počtem vrstevnic:
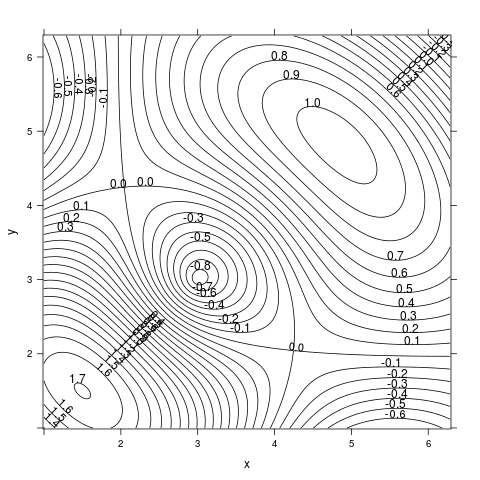
Obrázek 24: Změna rozsahu a hustoty vrstevnic.
Můžeme naopak určit, že se mají vykreslovat jen vrstevnice pro hodnoty větší než 0:
library("lattice")
x <- seq(1.0, 2*pi, length.out=200)
y <- seq(1.0, 2*pi, length.out=200)
r1 <- as.vector(sqrt(outer(x^2, y^2, "+")))
r2 <- as.vector(sqrt(outer((x-3)^2, (y-3)^2, "+")))
grid <- expand.grid(x=x, y=y)
grid$z <- sin(r1) + sin(r2)
contourplot(z ~ x * y, grid, col.regions = topo.colors(20),
at = c(-Inf, seq(0.0, 2.0, by = 0.1), Inf))
Výsledkem je tento graf:
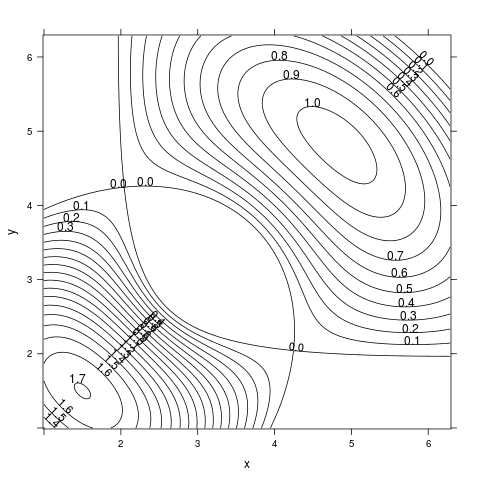
Obrázek 25: Změna rozsahu a hustoty vrstevnic.
A konečně si ukažme, jak se graf změní ve chvíli, kdy je k dispozici mnohem menší množství hodnot (100× méně):
library("lattice")
x <- seq(1.0, 2*pi, length.out=20)
y <- seq(1.0, 2*pi, length.out=20)
r1 <- as.vector(sqrt(outer(x^2, y^2, "+")))
r2 <- as.vector(sqrt(outer((x-3)^2, (y-3)^2, "+")))
grid <- expand.grid(x=x, y=y)
grid$z <- sin(r1) + sin(r2)
contourplot(z ~ x * y, grid, col.regions = topo.colors(20),
at = c(-Inf, seq(0.0, 2.0, by = 0.1), Inf))
Výsledek již nebude (podle očekávání) tak pěkný, jako v případech předchozích:
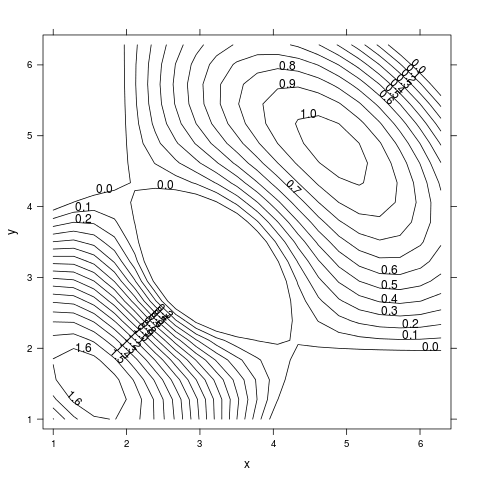
Obrázek 26: Malé množství hodnot pro výpočet vrstevnicového grafu.
13. Krabicový diagram
Dalším typem grafu, který knihovna Lattice podporuje, jsou takzvané krabicové diagramy. Tento typ diagramů nezobrazuje pouze naměřené či vypočtené hodnoty, ale vykreslí i kvartily. Ohraničení je vypočteno a zobrazeno na základě prvního a třetího kvartilu a navíc se zobrazuje i úsečka (vodorovná či svislá) představující medián. Podívejme se nyní na způsob vykreslení krabicového diagramu naležato – meze jsou tedy zobrazeny napravo a nalevo od zobrazované hodnoty:
library(lattice)
input <- mtcars[,c('wt','mpg','hp','gear','cyl')]
gear.f <- factor(input$gear,
levels = c(3,4,5),
labels = c("3gears","4gears","5gears"))
cyl.f <- factor(input$cyl,
levels=c(4,6,8),
labels=c("4cyl","6cyl","8cyl"))
bwplot(cyl.f~mpg|gear.f,
data = input,
ylab = "Cylinders",
xlab = "Miles per Gallon",
main = "Mileage by Cylinders and Gears",
layout = (c(1,3)))
S tímto výsledkem:
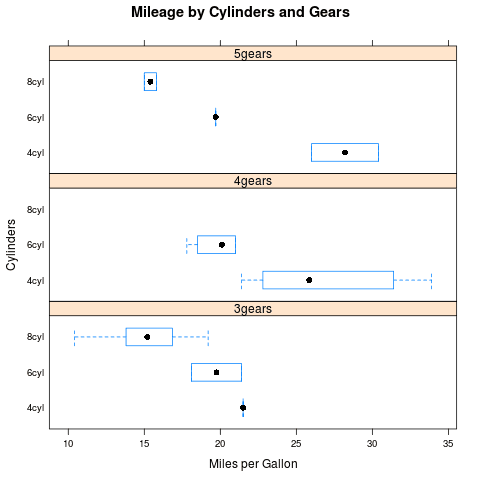
Obrázek 27: Jednoduchý krabicový diagram.
Odlišný krabicový diagram, tentokrát pro data získána z data setu iris:
library(lattice)
data("iris")
head(iris)
input <- iris[,c('Sepal.Length','Sepal.Width','Petal.Length','Petal.Width','Species')]
bwplot(Sepal.Width ~ Sepal.Length,
data = input,
auto.key = TRUE)
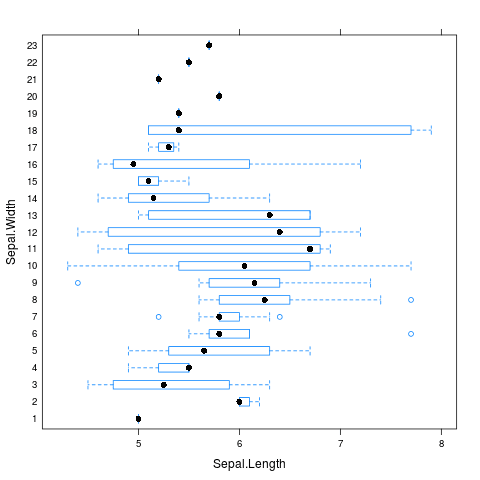
Obrázek 28: Další forma krabicového diagramu.
14. Zobrazení nastavení diagramů
Způsob vykreslení diagramů knihovnou Lattice lze ovlivnit, a to mnoha způsoby. Všechny důležité volby nastavení zobrazení je možné taktéž vykreslit do speciální grafu vyvolaného funkcí show.settings():
library(lattice) show.settings()
Výsledek by měl vypadat následovně:
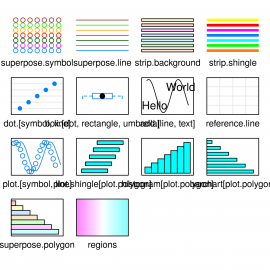
Obrázek 29: Zobrazení voleb ovlivňujících styl vykreslení grafů a diagramů.
15. Drátový (3D) diagram a jeho varianty
Posledním typem diagramu, který si dnes popíšeme, je takzvaný drátový (wireframe) diagram, který zobrazuje průběh funkce z=f(x,y), popř. naměřené či vypočtené hodnoty uložené do matice. Tento diagram je zobrazen funkcí wireframe, která se může volat se stejnými parametry jako výše zmíněný diagram levelplot. Podívejme se tedy na jednoduchý demonstrační příklad, který vychází z příkladů, které jsme si již ukazovali v předchozích kapitolách:
library(lattice)
x <- seq(-1.1*pi, 1.1 * pi, length.out = 30)
y <- seq(-1.1*pi, 1.1 * pi, length.out = 30)
r <- as.vector(sqrt(outer(x^2, y^2, "+")))
grid <- expand.grid(x=x, y=y)
grid$z <- cos(r)
wireframe(z ~ x * y, grid, col.regions = topo.colors(20),
at = c(-Inf, seq(-0.8, 0.8, by = 0.2), Inf))
Výsledný obrázek s grafem by měl vypadat následovně:
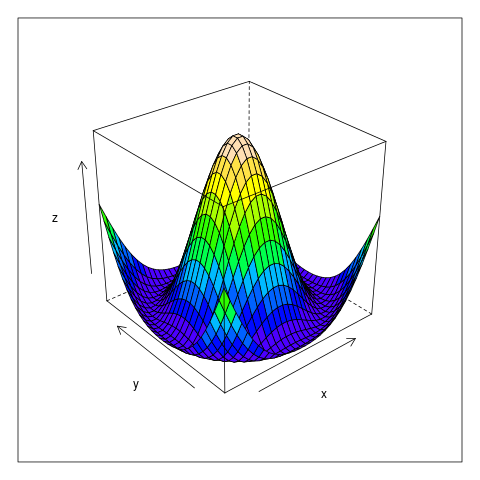
Obrázek 30: Drátový diagram s vyplněnými ploškami.
16. Knihovna ggplot2
V navazující části tohoto seriálu budou popsány základní koncepty, na nichž je postavena knihovna nazvaná ggplot2. Ta byla vytvořená v roce 2005 Hadleym Wickhamem ve formě balíku určeného pro programovací jazyk R, ovšem později došlo k rozšíření i pro další programovací jazyky. ggplot2 je založen na tvorbě grafů s využitím grammar of graphics popsané Lelandem Wilkinsonem. Tato gramatika umožňuje popisovat jednotlivé objekty, z nichž se graf skládá.
17. Ukázky základních možností knihovny ggplot2
Bez podrobnějšího popisu si ukažme základní možnosti knihovny ggplot2, a to na datech, která již známe:
library(ggplot2) qplot(wt, mpg, data = mtcars)
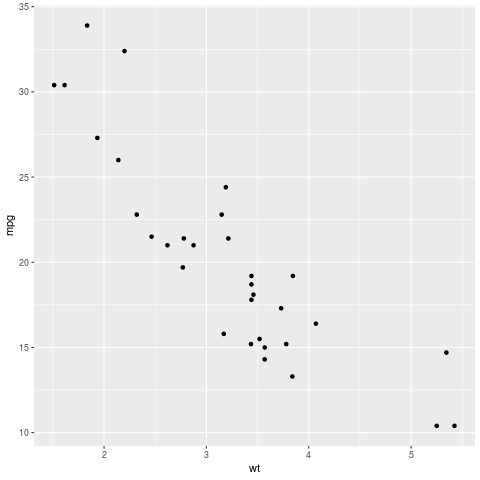
Obrázek 31: Graf vykreslený knihovnou ggplot2.
Popř. obarvená varianta:
library(ggplot2) qplot(wt, mpg, data = mtcars, colour = factor(cyl))
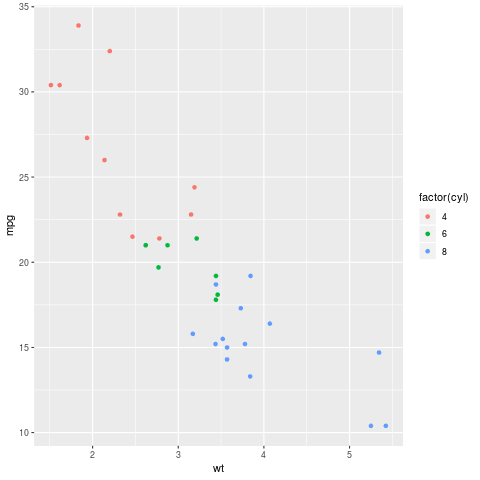
Obrázek 32: Další graf vykreslený knihovnou ggplot2
18. Obsah následující části seriálu
V navazující části seriálu o programovacím jazyku R si popíšeme základní koncepty, na nichž je postavena knihovna ggplot2. Tyto informace budou použitelné nejenom pro uživatele používající přímo jazyk R, ale i pro programátory, kteří ggplot2 volají z dalších programovacích jazyků.
19. Repositář s demonstračními příklady
Zdrojové kódy všech dnes použitých demonstračních příkladů byly uloženy do nového Git repositáře, který je dostupný na adrese https://github.com/tisnik/r-examples V případě, že z nějakého důvodu nebudete chtít klonovat celý repositář (ten je ovšem – alespoň prozatím – velmi malý, dnes má stále jen jednotky kilobajtů), můžete namísto toho použít odkazy na jednotlivé demonstrační příklady, které naleznete v následující tabulce:
20. Odkazy na Internetu
- The R Project for Statistical Computing
https://www.r-project.org/ - An Introduction to R
https://cran.r-project.org/doc/manuals/r-release/R-intro.pdf - R (programming language)
https://en.wikipedia.org/wiki/R_(programming_language) - The R Programming Language
https://www.tiobe.com/tiobe-index/r/ - R Graphics Second Edition
https://www.stat.auckland.ac.nz/~paul/RG2e/ - Grid
https://www.stat.auckland.ac.nz/~paul/grid/grid.html - Interactive Course: Data Visualization with lattice in R
https://www.datacamp.com/courses/data-visualization-in-r-with-lattice - Lattice: trellis graphics for R
https://lattice.r-forge.r-project.org/ - Lattice: Multivariate Data Visualization with R
http://lmdvr.r-forge.r-project.org/figures/figures.html - Getting Started with Lattice Graphics
https://lattice.r-forge.r-project.org/Vignettes/src/lattice-intro/lattice-intro.pdf - Using lattice’s xyplot()
https://homerhanumat.github.io/tigerstats/xyplot.html - ggplot2 Tutorial
https://www.tutorialspoint.com/ggplot2/index.htm - Lattice Package in R with Functions and Graphs
https://techvidvan.com/tutorials/lattice-package-in-r/ - The R Graph Gallery
https://www.r-graph-gallery.com/index.html - Lattice Graphs
https://www.statmethods.net/advgraphs/trellis.html - ggplot2 (Graph gallery)
https://www.r-graph-gallery.com/ggplot2-package.html - R Markdown
https://rmarkdown.rstudio.com/ - R Markdown: The Definitive Guide
https://bookdown.org/yihui/rmarkdown/ - R Markdown Cheat Sheet
https://rstudio.com/wp-content/uploads/2016/03/rmarkdown-cheatsheet-2.0.pdf - Introduction to R Markdown
https://rmarkdown.rstudio.com/articles_intro.html - R Cheat Sheets
https://blog.sergiouri.be/2016/07/r-cheat-sheets.html - R Cheat Sheet
https://s3.amazonaws.com/quandl-static-content/Documents/Quandl±+R+Cheat+Sheet.pdf - Base R Cheat Sheet
https://rstudio.com/wp-content/uploads/2016/06/r-cheat-sheet.pdf - PYPL PopularitY of Programming Language
https://pypl.github.io/PYPL.html - Tiobe index
https://www.tiobe.com/tiobe-index/ - Stack Overflow: Most Loved, Dreaded & Wanted Programming Languages In 2020
https://fossbytes.com/stack-overflow-most-loved-dreaded-wanted-programming-languages-in-2020/ - How to Install and Use R on Ubuntu
https://itsfoss.com/install-r-ubuntu/ - R programming for beginners – Why you should use R
https://www.youtube.com/watch?v=9kYUGMg_14s - GOTO 2012 • The R Language The Good The Bad & The Ugly
https://www.youtube.com/watch?v=6S9r_YbqHy8 - R vs Python – What should I learn in 2020? | R and Python Comparison
https://www.youtube.com/watch?v=eRP_J2yLjSU - R Programming 101
https://www.youtube.com/c/rprogramming101 - Seriál Tvorba grafů pomocí programu „R“
https://www.root.cz/serialy/tvorba-grafu-pomoci-programu-r/ - Tvorba grafů pomocí programu „R“: úvod
https://www.root.cz/clanky/tvorba-grafu-pomoci-programu-r-1/ - Tvorba grafů pomocí programu „R“: pokročilé funkce
https://www.root.cz/clanky/tvorba-grafu-pomoci-programu-r-pokrocile-funkce/ - Tvorba grafů pomocí programu „R“: vkládání textu, čeština
https://www.root.cz/clanky/grafy-pomoci-programu-r-vkladani-textu-cestina/ - Cesta erka: Krok nultý – instalace & nastavení – prostředí, projekty, package
https://www.jla-data.net/r4su/r4su-environment-setup/ - Cesta erka: Krok první – operace a struktury – proměnné, rovnítka a dolary
https://www.jla-data.net/r4su/r4su-data-structures/ - Cesta erka: Krok druhý – načtení externích dat – csvčka, excely a databáze
https://www.jla-data.net/r4su/r4su-read-data/ - Cesta erka: Krok třetí – manipulace s daty – dplyr, slovesa a pajpy
https://www.jla-data.net/r4su/r4su-manipulate-data/ - Cesta erka: Krok čtvrtý – podání výsledků – ggplot, geomy a estetiky
https://www.jla-data.net/r4su/r4su-report-results/ - Cesta erka: Krok pátý – case study – případ piva v Praze
https://www.jla-data.net/r4su/r4su-case-study-beer/ - V indexu popularity programovacích jazyků TIOBE překvapilo R, Go, Perl, Scratch a Rust
https://www.root.cz/zpravicky/v-indexu-popularity-programovacich-jazyku-tiobe-prekvapilo-r-go-perl-scratch-a-rust/ - Is R Programming SURGING in Popularity in 2020?
https://www.youtube.com/watch?v=Duwn-vImyXE - Using the R programming language in Jupyter Notebook
https://docs.anaconda.com/anaconda/navigator/tutorials/r-lang/ - Using R on Jupyter Notebook
https://dzone.com/articles/using-r-on-jupyternbspnotebook - Graphics, ggplot2
http://r4stats.com/examples/graphics-ggplot2/ - A Practice Data Set
https://r4stats.wordpress.com/examples/mydata/ - Shiny – galerie projektů
https://shiny.rstudio.com/gallery/ - Seriál Programovací jazyk Julia
https://www.root.cz/serialy/programovaci-jazyk-julia/ - Julia (front page)
http://julialang.org/ - Julia – repositář na GitHubu
https://github.com/JuliaLang/julia - Julia (programming language)
https://en.wikipedia.org/wiki/Julia_%28programming_language%29 - IJulia
https://github.com/JuliaLang/IJulia.jl - Introducing Julia
https://en.wikibooks.org/wiki/Introducing_Julia - Julia: the REPL
https://en.wikibooks.org/wiki/Introducing_Julia/The_REPL - Introducing Julia/Metaprogramming
https://en.wikibooks.org/wiki/Introducing_Julia/Metaprogramming - Month of Julia
https://github.com/DataWookie/MonthOfJulia - Learn X in Y minutes (where X=Julia)
https://learnxinyminutes.com/docs/julia/ - New Julia language seeks to be the C for scientists
http://www.infoworld.com/article/2616709/application-development/new-julia-language-seeks-to-be-the-c-for-scientists.html - Julia: A Fast Dynamic Language for Technical Computing
http://karpinski.org/publications/2012/julia-a-fast-dynamic-language - The LLVM Compiler Infrastructure
http://llvm.org/ - Julia: benchmarks
http://julialang.org/benchmarks/ - R Vector
https://www.datamentor.io/r-programming/vector/ - .R File Extension
https://fileinfo.com/extension/r - Lineární regrese
https://cs.wikipedia.org/wiki/Line%C3%A1rn%C3%AD_regrese - lm (funkce)
https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/lm - quit (funkce)
https://www.rdocumentation.org/packages/base/versions/3.6.2/topics/quit - c (funkce)
https://www.rdocumentation.org/packages/base/versions/3.6.2/topics/c - help (funkce)
https://www.rdocumentation.org/packages/utils/versions/3.6.2/topics/help - Shiny: Introduction to interactive documents
https://shiny.rstudio.com/articles/interactive-docs.html - R Release History 1997–2013
http://timelyportfolio.github.io/rCharts_timeline_r/ - R: atomic vectors
https://renenyffenegger.ch/notes/development/languages/R/data-structures/vector/ - 11 Best R Programming IDE and editors
https://www.dunebook.com/best-r-programming-ide/ - CRAN – The Comprehensive R Archive Network
https://cran.r-project.org/ - R – Arrays
https://www.tutorialspoint.com/r/r_arrays.htm - Array vs Matrix in R Programming
https://www.geeksforgeeks.org/array-vs-matrix-in-r-programming/?ref=rp - Online R Language IDE
https://www.jdoodle.com/execute-r-online/ - Execute R Online (R v3.4.1)
https://www.tutorialspoint.com/execute_r_online.php - Snippets: Run any R code you like. There are over twelve thousand R packages preloaded
https://rdrr.io/snippets/ - R Package Documentation
https://rdrr.io/ - Data Reshaping in R – Popular Functions to Organise Data
https://techvidvan.com/tutorials/data-reshaping-in-r/ - What is an R Data Frame?
https://magoosh.com/data-science/what-is-an-r-data-frame/ - What's a data frame?
https://campus.datacamp.com/courses/free-introduction-to-r/chapter-5-data-frames?ex=1 - data.frame
https://www.rdocumentation.org/packages/base/versions/3.6.2/topics/data.frame - as.data.frame
https://www.rdocumentation.org/packages/base/versions/3.6.2/topics/as.data.frame - table
https://www.rdocumentation.org/packages/base/versions/3.6.2/topics/table - Python Pandas – DataFrame
https://www.tutorialspoint.com/python_pandas/python_pandas_dataframe.htm - The Pandas DataFrame: Make Working With Data Delightful
https://realpython.com/pandas-dataframe/ - Python | Pandas DataFrame
https://www.geeksforgeeks.org/python-pandas-dataframe/ - R – Factors
https://www.tutorialspoint.com/r/r_factors.htm - R – Scatterplots
https://www.tutorialspoint.com/r/r_scatterplots.htm - Quick guide to line types (lty) in R
https://www.benjaminbell.co.uk/2018/02/quick-guide-to-line-types-lty-in-r.html - Lattice C (Wikipedia)
https://en.wikipedia.org/wiki/Lattice_C - Lorenz Attractor in R
https://www.sixhat.net/lorenz-attractor-in-r.html - Small multiple
https://en.wikipedia.org/wiki/Small_multiple - Category:Infographics (infografika)
https://en.wikipedia.org/wiki/Category:Infographics - Trellis plots (pro Python)
https://subscription.packtpub.com/book/big_data_and_business_intelligence/9781784390150/4/ch04lvl1sec41/trellis-plots - Trellis (architecture)
https://en.wikipedia.org/wiki/Trellis_(architecture) - Izobara (meteorologie)
https://cs.wikipedia.org/wiki/Izobara_(meteorologie) - How to Create a Lattice Plot in R
https://www.dummies.com/programming/r/how-to-create-a-lattice-plot-in-r/ - Density estimation
https://en.wikipedia.org/wiki/Density_estimation - Sedm smrtelných statistických hříchů
http://dfens-cz.com/sedm-smrtelnych-statistickych-hrichu/ - Spurious correlations
https://tylervigen.com/spurious-correlations






































