Obsah
1. Rekurzivní procedura určená pro vykreslení C-křivky
2. Globální proměnné a práce s nimi
3. Procedura make
4. Procedura thing a vertikální seznamy
5. Kresba pravoúhlého trojúhelníku se zadaným úhlem a délkou přepony
6. Zobecněný Pythagorův strom
7. Animace zobecněného Pythagorova stromu
8. Obsah následující části tohoto seriálu
1. Rekurzivní procedura určená pro vykreslení C-křivky
V předchozí části seriálu o programovacím jazyku Logo jsme si ukázali, jakým způsobem je možné použít rekurzivně volané procedury společně s želví grafikou pro vykreslení některých zajímavých obrázků, které se vyznačovaly soběpodobností (jinými slovy – jednalo se o fraktály). Na demonstračních příkladech byla vysvětlena tvorba fraktální křivky Helge von Kocha, sněhové vločky Helge von Kocha, dvou variant Sierpinského trojúhelníku a základní formy Pythagorova stromu. Dnes toto téma dokončíme. V první kapitole bude popsána takzvaná C-křivka, v šesté kapitole si ukážeme tvorbu zobecněného Pythagorova stromu a v kapitole sedmé animaci zobecněného Pythagorova stromu, která je provedena postupnou změnou úhlu odklonu jeho větví.
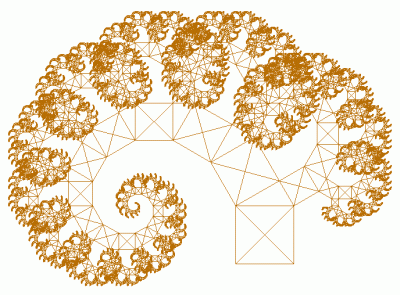
Začneme popisem C-křivky (C-curve). Jedná se o fraktální objekt vykreslený jednou lomenou čarou (polyčarou). Úhel „zalomení“ této polyčáry je vždy roven devadesáti stupňům a všechny úsečkové segmenty, ze kterých je polyčára složena, mají stejnou délku. Při bližším pohledu na celou konstrukci (viz první tři obrázky) zjistíme, že jde o rekurzivní křivku, tj. při každé iteraci se původní úsečkové segmenty rozdělí na dvě C-křivky, přičemž na poslední úrovni se pouze vykreslí horizontální či vertikální čára (podle aktuální orientace želvy). Při nastavení maximální úrovně iterace na nulu se vykreslí pouze vertikální úsečka (provede se kód za příkazem if), nastavení úrovně na jedničku má za následek vykreslení dvou na sebe kolmých úseček, při úrovni nastavené na dvojku se již vykreslí základ písmena „C“ atd. Procedura, která kreslí tuto křivku, má ve své nejjednodušší podobě následující tvar:
to c_krivka :velikost :uroven
if :uroven <= 0 [
forward :velikost
stop
]
c_krivka :velikost :uroven-1
right 90
c_krivka :velikost :uroven-1
left 90
end 

2. Globální proměnné a práce s nimi
Před vysvětlením způsobu vykreslení zobecněného Pythagorova stromu se musíme seznámit s konceptem globálních proměnných. V Logu jsou proměnné rozlišovány na lokální a globální. Globální proměnné existují v adresovém prostoru interpreteru Loga pouze jedenkrát a jsou společné pro všechny procedury, které potřebují hodnoty z těchto proměnných číst nebo do nich naopak zapisovat (standardní Logo nepracuje s moduly ani s prostory jmen). Naproti tomu lokální proměnné existují pouze uvnitř nějaké procedury a „zvenčí“ k nim není možné přistupovat. Přesněji řečeno – tyto proměnné jsou dostupné i volaným procedurám, tj. o viditelnosti je rozhodováno v době běhu programu (runtime) – jde tedy o chování, kterým se Logo odlišuje například od Céčka, Pascalu či Javy, kde je viditelnost proměnných řešena už v době překladu (compile time).
Jako v jiných programovacích jazycích, i v Logu je vhodné použití globálních proměnných omezit a spíše používat předávání hodnot do procedur pomocí parametrů, například seznamů, kterými je možné nahradit jak struktury (záznamy), tak i pole. Z pohledu programátora znajícího některý z kompilovaných jazyků typu C, C++, Javy či Pascalu, je Logo odlišné v tom, že proměnné není zapotřebí deklarovat ani jim explicitně přiřadit nějaký datový typ. Datový typ totiž není přiřazen proměnné, ale přímo hodnotě, která je v nějaké proměnné uložena. Tento způsob práce s datovými typy se nazývá dynamické typování a jedná se o jednu z charakteristických vlastností mnoha starších i moderních skriptovacích jazyků – LISPu, Scheme, Loga, Pythonu atd.
Proč je tato vlastnost jazyka nazývána dynamické typování? Jedna proměnná může v různých částech programu, nebo i ve stejné části programu v jiném čase, obsahovat hodnoty různého typu, ovšem s tím, že vždy můžeme zjistit (například pomocí takzvaných predikátů, které se poprvé objevily už v LISPu), jakého typu daná hodnota je. Nejedná se tedy o slabé typování (loose typing), které také bývá v jiných programovacích jazycích použito a u něhož se sice proměnným typy přiřazují (například jejich deklarací, tj. typicky v době překladu), ale je možné provádět typově nekorektní operace (z tohoto pohledu i Céčko může být považováno za slabě typovaný jazyk).

3. Procedura make
Přiřazení hodnoty do proměnné se v Logu neprovádí pomocí operátoru přiřazení, ale zavoláním procedury make. Prvním parametrem této procedury je jméno proměnné a druhým parametrem hodnota, která se do této proměnné má přiřadit. Při zadávání jména proměnné je nutné před toto jméno vložit znak „ (“počítačové" uvozovky), čímž je zajištěno, že interpreter Loga nebude toto jméno chápat jako volání jiné procedury (ovšem i to je v Logu dovoleno – můžeme napsat proceduru, která vrátí jméno proměnné, do které se posléze pomocí make přiřadí hodnota). Ukažme si vše na jednoduchém příkladu, ve kterém je do proměnné nazvané "foo vložena celočíselná hodnota 42 a do proměnné "bar seznam obsahující čísla 1, 2, 3, 4 a 5:
make "foo 42
make "bar [1, 2, 3, 4, 5]
4. Procedura thing a vertikální seznamy
Pro zpětné vyčtení hodnoty uložené do nějaké proměnné je určena procedura thing, jíž se jako parametr předá jméno proměnné, které musí opět začínat uvozovkou (ve skutečnosti jsou procedury make i thing takzvané speciální formy, pro jejich vlastní naprogramování by se použila makra podobná těm z LISPu). Procedura thing načte zadané jméno proměnné a vrátí její hodnotu. Můžeme si to ihned vyzkoušet: pomocí procedury show či print je možné vypsat hodnotu libovolného výrazu, samozřejmě včetně hodnoty proměnné. Je tedy možné napsat následující kód (řádky zapsané kurzívou zpětně vypisuje interpreter Loga):
show 1*2*3
6
show thing "foo
42 Pokud se však podíváme na zdrojové kódy aplikací psaných v Logu, tak zjistíme, že se v nich procedura thing prakticky nevyskytuje. To je jistě podivné, protože načítání hodnoty z proměnné je operace, která se v programech vyskytuje velmi často, ostatně to je také důvod, proč proměnné existují. Ovšem vzhledem k tomu, že všichni dobří programátoři jsou líní :-), je už od prvních verzí Loga povolen zkrácený zápis dvojice symbolů thing " za jediný znak : (dvojtečka, anglicky colon, ale uživatelé pracující s Logem tento znak raději nazývají dots). Následující dva programové řádky tedy provádí stejnou činnost, ovšem druhý z nich je čitelnější a také častěji používaný:
show thing "foo
42
show :foo
42 Osobně se mi tento způsob práce s proměnnými příliš nezamlouvá, ale důvod pro zavedení dvou znaků vkládaných před jména proměnných je dán historickými důvody: jak procedury, tak i proměnné sdílí stejný prostor jmen (jako v LISPu), a proto je nutné je odlišit. Některé interpretery Loga dovolují v určitých případech vynechat znak uvozovek, ale pouze tehdy, jestliže není proměnná pojmenována stejně jako nějaká procedura (potom by bez uvedení uvozovek došlo ke kolizi jmen a místo proměnné by se volala/vyhodnotila stejně pojmenovaná procedura). Na druhou stranu nám notace podporovaná v Logu umožňuje jednoduše vytvářet procedury, které mohou měnit obsah proměnných, které jim byly předány jako parametry:
to increment :promenna
; v příkazu make je uvedeno :promenna a nikoli "promenna
; protože se nejedna přímo o název proměnné, ten je naopak
; v této proměnné uložen (v podstatě se jedná o řetězec)
make :promenna (thing :promenna)+1
; thing :promenna je zajímavý zápis, protože se ve skutečnosti
; jedná o vnořené volání procedury thing (viz význam znaku dvojtečka)
end
make "foo 42
show :foo
42
increment "foo
show :foo
43 Se jmény proměnných je možné provádět i další „kouzla“. Jedna proměnná může obsahovat jméno jiné proměnné, která obsahuje jméno proměnné další, atd. Takovým způsobem je možné vytvářet seznamy, které se narozdíl od seznamů podporovaných přímo jazykem nazývají vertikální seznamy. Podívejme se na rozdíl mezi následující dvojicí přiřazovacích příkazů:
make "x 42
make "y :x
; proměnná x i y nyní obsahuje hodnotu 42, což lze znázornit takto:
x ---> 42
y ---> 42
make "x 42
make "y "x
; proměnná y nyní obsahuje jméno proměnné x, což můžeme znázornit:
x ---> 42
y ---> x ---> 42
; a o pravdivosti se můžeme přesvědčit například sekvencí příkazů:
show :x
42
show :y
x
show thing thing "y
42
show thing :y
42 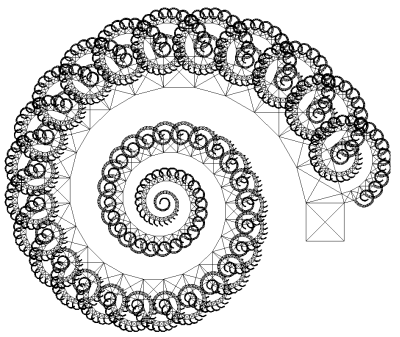
5. Kresba pravoúhlého trojúhelníku se zadaným úhlem a délkou přepony
Při kresbě zobecněného Pythagorova stromu je nutné vytvořit proceduru, která dokáže nakreslit pravoúhlý trojúhelník o zadané délce přepony (nejdelší strany) a úhlu mezi přeponou a jednou odvěsnou. Proč potřebujeme vytvořit takovou proceduru? Zobecněný Pythagorův strom se od pravidelného Pythagorova stromu, který jsme si popsali v předchozí části tohoto seriálu, odlišuje především v tom, že je použit jiný úhel větvení, což jinými slovy znamená, že se změní tvar střechy z rovnoramenného pravoúhlého trojúhelníku na jiný pravoúhlý trojúhelník. Délka přepony v tomto trojúhelníku odpovídá šířce „domku“, který tvoří základ celého stromu, a odvěsny představují obě plochy střechy. Změnou úhlu odchylky první odvěsny se změní i tvar celého trojúhelníku.
Výpočet délky odvěsen je velmi jednoduchý. První odvěsna bude mít délku rovnou:
a=c×cos α
a druhá odvěsna:
b=c×sin α
kde α je úhel, který svírá odvěsna a s přeponou c.
Pokud již známe vzorce pro výpočet délky obou odvěsen, je již snadné napsat proceduru, která střechu skutečně vykreslí. V Logu je možné volat základní goniometrické funkce sinus a kosinus, jimž je jako parametr předán úhel ve stupních (Logo zde zachovává konzistenci – otočení želvy se zadává ve stupních a totéž platí i pro goniometrické funkce). Pro testovací účely jsem vytvořil proceduru nazvanou strecha, která akceptuje dva parametry: délku odvěsny, tj. šířku domku a úhlu mezi stranami a a c. Procedura strecha má následující tvar:
to strecha :delka :uhel
right 90
left :uhel
forward :delka * cos :uhel
right 90
forward :delka * sin :uhel
end Tuto proceduru je vhodné otestovat pro úhly menší než 90°. Pro tyto účely slouží následující program, který vykreslí všechny střechy (bez základny) pro úhly ležící v rozsahu 5° až 85° s krokem 2°. To, že procedura strecha pracuje korektně, je patrné z toho, že každá dvojice úseček začíná a končí ve stejném bodě (správně se spočítaly délky) a všechny vrcholy trojúhelníků leží na stejné kružnici (jedná se tedy o trojúhelníky pravoúhlé). Celý testovací program má tvar:
to strecha :delka :uhel
right 90
left :uhel
forward :delka * cos :uhel
right 90
forward :delka * sin :uhel
end
to test_strecha :delka :uhel_min :uhel_max :uhel_delta
make "uhel :uhel_min
repeat (:uhel_max-:uhel_min)/:uhel_delta [
pu
setpos [-250 0]
setheading 0
pd
strecha :delka :uhel
make "uhel :uhel+:uhel_delta
]
end
(draw 500 500)
ht
clean
test_strecha 550 5 85 2 
6. Zobecněný Pythagorův strom
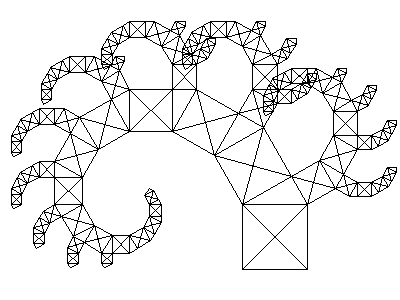
Se znalostí tvorby střechy se zadaným úhlem sklonu jedné její strany se můžeme pustit do úprav procedury pro vykreslení Pythagorova stromu. Úpravy se kupodivu dotknou pouze malé části kódu. Samozřejmě bude přidán další parametr :uhel. Dále se změní příkaz pro natočení želvy před kreslením střechy (jde o hodnotu 90°-uhel), příkaz pro natočení želvy po kreslení střechy (přímo hodnota uhel) a konečně se změní i výraz, kterým je počítána délka obou stran střechy. Místo výrazu :stranasqrt 2 se použijí výrazy :stranacos :uhel pro první stranu střechy a :strana*sin :uhel pro druhou stranu. To je vše – nyní je procedura domek připravena kreslit zobecněný Pythagorův strom, jehož tři varianty jsou zobrazeny na obrázcích 7, 8 a 9:
to domek :strana :uhel
ifelse :strana>10 [
; základna
forward :strana
; úhlopříčka
left 90+45
forward :strana*sqrt 2
; stěna
left 90+45
forward :strana
; úhlopříčka
left 90+45
forward :strana*sqrt 2
; úsečka pod střechou
left 90+45
forward :strana
; první část střechy
right 90
right 90-:uhel
; původní příkaz: domek :strana/sqrt 2 :uhel
domek :strana*cos :uhel :uhel
; druhá část střechy
right 90
; původní příkaz: domek :strana/sqrt 2 :uhel
domek :strana*sin :uhel :uhel
; zbývající stěna
right :uhel
forward :strana left 90
] [
forward :strana
]
end
draw
setpos [0 -100]
clean
right 90
domek 70 30 

7. Animace zobecněného Pythagorova stromu
Postupnou změnu úhlu náklonu střechy, a tím i odklonu jednotlivých větví Pythagorova stromu, je možné vytvořit jednoduchou animaci. V úvodních částech tohoto seriálu jsem se zmínil o tom, že implementace Loga nazvaná MSW Logo (Microsoft Windows Logo, nejedná se však o program firmy Microsoft) umožňuje vytváření animací ukládaných do grafických souborů typu GIF (Graphics Interchange File Format). Tyto animace lze bez dalších optimalizací prezentovat například na webu, protože se v případě kresby želví grafikou jedná o poměrně kompaktní soubory. Následující program je určen právě pro MSW Logo. Po jeho spuštění se vytvoří animace obsahující 71 snímků, přičemž každý snímek má rozlišení 300×300 pixelů, bitovou hloubku 1 (černobílý obrázek) a doba trvání snímku je nastavena na 15 ms. Po odstranění příkazů (gifsave …) je samozřejmě možné program spustit na libovolné implementaci Loga, animace ovšem bude probíhat pouze na obrazovce a neuloží se do externího souboru.

to domek :iter :strana :uhel
ifelse :iter>0 [
; základna
forward :strana
; úhlopříčka
left 90+45
forward :strana*sqrt 2
; stěna
left 90+45
forward :strana
; úhlopříčka
left 90+45
forward :strana*sqrt 2
; úsečka pod střechou
left 90+45
forward :strana
; první část střechy
right 90
right 90-:uhel
domek :iter-1 :strana*cos :uhel :uhel
; druhá část střechy
right 90
domek :iter-1 :strana*sin :uhel :uhel
; zbývající stěna
right :uhel
forward :strana left 90
] [
forward :strana
]
end
; vytvoření animace - platí pouze pro MSW Logo!
to anim
cs
; vytvoření kontejneru pro ukládání dalších snímků
(gifsave "myfile.gif 15 "False 0 1)
make "uhel 10
; zde je možné nahradit cyklus rekurzí
repeat 70 [
; nastavení želvy vždy do stejné počáteční pozice
setpos [-35 -100]
setheading 0
clean
right 90
domek 6 70 :uhel
; zvýšení hodnoty úhlu
make "uhel :uhel+1
; a připojení snímku do animace
(gifsave "myfile.gif 15 "True 1)
]
end
; spuštění animace
anim 
8. Obsah následující části tohoto seriálu
V příští části seriálu o programovacím jazyce Logo si podrobněji řekneme, jaké matematické a logické funkce je možné při programování volat a na závěr bude demonstrován příklad použití generátoru náhodných čísel (RNG – Random Number Generator), který je možné použít v mnoha algoritmech, především ve spojení se želví grafikou.