Programujeme JPEG: Kvantizace DCT koeficientů

Obsah

1. Urychlení výpočtů diskrétní kosinové transformace
2. Operace prováděné po diskrétní kosinové transformaci
3. Kvantizace DCT koeficientů
4. Kvantizační tabulky
5. Zpracování stejnosměrných složek (DC)
6. Linearizace kvantovaných koeficientů pomocí cik-cak sekvence
7. Obsah dalšího pokračování tohoto seriálu

1. Urychlení výpočtů diskrétní kosinové transformace

V předchozí části tohoto seriálu jsme si řekli, že DCT transformace je zcela jistě nejtypičtějším rysem ztrátové komprimace pomocí standardu JPEG a standardů navazujících (MPEG-1 apod.). Současně se však také jedná o operaci poměrně výpočetně náročnou, proto byly a dodnes jsou hledány metody vedoucí k urychlení a/nebo zjednodušení výpočtů DCT. Samotný standard JPEG nám neříká, jakým způsobem se má DCT provádět, pouze uvádí základní tvar vzorců. Když se nad tímto stavem zamyslíme, zjistíme, že je vlastně logický: komise tvořící standard JPEG nemohla vědět, na jakých zařízeních budou kodéry i dekodéry pro JPEG v budoucnosti implementovány a jaké budou možnosti použitých procesorů. Například na kodér tvořený pro současné výkonné mikroprocesory budou kladeny jiné požadavky (počet obsazených registrů, počet instrukcí čtení z paměti, možnost použití reálné aritmetiky) než na kodér implementovaný na DSP (minimalizace skoků, linearizace kódu, instrukce typu VLIW) nebo dokonce realizovaný přímo na programovatelném čipu pomocí VHDL (redukce násobiček) atd.

V průběhu vývoje bylo vytvořeno mnoho způsobů, jakými je možné DCT a inverzní DCT provést. Nelze říci, který způsob je nejvýhodnější, vždy záleží na konkrétní implementaci. Některé způsoby jsou – jak už se ve světě souborových formátů stalo samozřejmostí – zatíženy patenty, proto je jejich použití (například pro GNU software) limitováno. Následuje stručný výpis nejznámějších metod implementace DCT a inverzní DCT:

1. Rekurzivní výpočet DCT používající reálnou aritmetiku (takzvaný Chenův algoritmus). Vhodné v případě implementace DCT na zařízení s matematickým koprocesorem.
2. Další verze efektivního rekurzivního algoritmu (takzvaný Leeův algoritmus). Jedná se o obvodovou úpravu algoritmu pro výpočet FFT pomocí známého „motýlku“ firmou Thomson Microelectronics.
3. Existují také rychlé algoritmy, které však jdou použít v případě, že N je prvočíslo (3, 5, 7, …). V tomto případě dochází k výraznému snížení počtu operací, což činí tyto postupy vhodné zejména pro HW realizaci. Pro JPEG se tyto algoritmy nepoužívají, ale je možné je použít v jiných případech, ve kterých se data transformují pomocí DCT.
4. Výpočet N-bodové DCT pomocí 2N-bodové FFT bez uvažování imaginárních složek výsledku. FFT (resp. přesněji DFT) je velmi známá a dlouho používaná transformace, proto jsou pro ni známé i optimální postupy výpočtu. DCT je s FFT velmi podobná, není tedy divu, že se objevují algoritmy pro výpočet DCT založené právě na známé FFT.
5. Výpočet N-bodové DCT pomocí N-bodové FFT. Na první pohled algoritmus podobný algoritmu předchozímu používá, ve skutečnosti jsou však použity zcela jiné výpočty.
6. Výpočet DCT pomocí Hartleyovy transformace.
7. Výpočet DCT pomocí WHT.

Na následujících dvou obrázcích je ukázáno, že DCT (v tomto případě osmibodovou 1D DCT) je možné realizovat s využitím opravdu minimálního množství násobiček. To se projeví zejména při hardwarové implementaci DCT a IDCT.

Obrázek 1: Blok výpočtu osmibodové 1D DCT

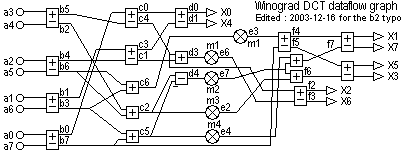
Obrázek 2: Optimalizace výpočetního řetězce tak, aby se minimalizovalo množství násobiček

2. Operace prováděné po diskrétní kosinové transformaci

Ústřední částí ztrátové komprimace JPEG je kvantování koeficientů vypočtených v předešlém bloku pomocí diskrétní kosinové transformace. Z předchozí části tohoto seriálu již víme, že výsledkem DCT jsou bloky o velikosti 8×8 hodnot. U typických obrázků (fotek, skenů, rentgenových snímků apod.) se největší hodnoty nachází v koeficientech reprezentujících stejnosměrnou složku a také nesoucích informaci o amplitudách kosinusových průběhů malých frekvencí. Vyšší frekvence se v obrázcích samozřejmě také vyskytují (například na hranách objektů umístěných v obrázku nebo u textu), tyto části obrázku jsou však nejvíce postiženy ztrátovou komprimací a dochází k jejich mnohdy na první pohled viditelnému rozmazání.

Tato ztráta je ve značné míře způsobena právě kvantováním koeficientů, v menší míře se může projevovat podvzorkování barvonosných složek C a C_r. Každá položka v bloku 8×8 hodnot je celočíselně vydělena hodnotami uloženými v takzvaných kvantizačních tabulkách (jedná se o dělení typu „položka po položce“). Pro správnou funkci kvantizace je důležité, aby DCT nebyla prováděna přímo nad daty získanými po převodu do barvového prostoru YC_bC_r, ale s koeficienty posunutými buď o hodnotu 128 (8bitové vzorky) nebo o hodnotu 2048 (12bitové vzorky) směrem k zápornému nekonečnu. Do DCT tedy vstupují hodnoty z rozsahu –128..127 nebo –2048..2047.

Obrázek 3: Blok kvantování DCT koeficientů pomocí kvantizačních tabulek

3. Kvantizace DCT koeficientů

Kvantizační tabulky jsou vytvořeny tak, aby obsahovaly nízké hodnoty u stejnosměrné složky i koeficientů amplitud kosinusových průběhů nízkých frekvencí a naopak vysoké hodnoty u koeficientů amplitud vysokých frekvencí. Výsledkem dělení je nový blok 8×8 hodnot, který většinou obsahuje u vysokých frekvencí nulové hodnoty (nezapomeňme, že se používá celočíselné dělení, právě zde dochází k největší – ale v podstatě ke kýžené – ztrátě informace). Právě ve vytvoření nulových hodnot spočívá význam DCT a kvantování: sady nulových hodnot jsou velmi dobře kódovatelné pomocí Huffmanova i aritmetického kódování.

Blok 8×8 hodnot se navíc po provedení kvantizace prochází metodou cik-cak (zig-zag), takže se nulové hodnoty většinou nachází za sebou či v těsné blízkosti, což dále zefektivňuje kódovací rutiny a nabízí použití slovníkových metod (viz následující části tohoto seriálu). Na správné volbě kvantizačních tabulek závisí jak komprimační poměr, tak i kvalita výsledného obrázku, proto je dnes vytvořeno několik knihoven (kódových knih) kvantizačních tabulek získaných zpracováním velkého množství obrazového materiálu. Když za nic jiného, tak v tomto případě je zapotřebí skupinu JPEG pochválit, protože navrhovanou metodu opravdu v praxi otestovala na velkém množství případů (fotky, faksimile, rentgenové snímky, družicové snímky atd.). Použitelnost JPEG je tedy doložena praktickými výsledky, nejedná se o návrh od „zeleného stolu“ (dnes oblíbený například W3C).

Příklad praktického použití kvantizačních tabulek je uveden na čtvrtém obrázku. Vlastní kvantizace se provádí způsobem „složka po složce“, tj. například hodnotu AC_3,3 vydělíme odpovídající hodnotou Q_3,3. Je použito dělení se zaokrouhlením na nejbližší celé číslo:

N_i,j=round(A_i,j/Q_i,j)

kde N je matice takzvaných normalizovaných DCT koeficientů, AC je matice barev pixelů (jedna ze složek Y, C_b, C_r) transformovaná pomocí DCT a Q je kvantizační matice.

Obrázek 4: Příklad provedení kvantizace DCT koeficientů

4. Kvantizační tabulky

Nyní se podívejme na to, jakým způsobem bývají navrženy kvantizační tabulky. V předchozích pokračováních tohoto seriálu jsme si řekli, že u typických obrázků se hodnoty důležité pro rozpoznání obrázku lidským vizuálním systémem (HVS – human visual system) nachází v DCT koeficientech reprezentujících stejnosměrnou složku a také amplitudy kosinusových průběhů malých frekvencí. Vyšší frekvence se ve zpracovávaných obrázcích samozřejmě také vyskytují, u fotek se většinou jedná o normální šum či hrany, u kterých se projeví rozmazání a „kostičkování“ (zviditelnění bloků 8×8 pixelů). Při návrhu kvantizačních tabulek je velmi důležité vědět, jakou strukturu obrázku reprezentuje příslušný DCT koeficient. Pro první přiblížení celého problému se podívejme na následující ilustrační obrázek, který ukazuje zastoupení jednotlivých typů obrázkových struktur (typických tvarů) v bloku DCT koeficientů (čím větší je velikost bloku zpracovávaný 2D DCT, tím blíže jsou výsledky k uvedenému obrázku):

Obrázek 5: Zastoupení jednotlivých typů obrázkových struktur v bloku DCT koeficientů

Kvantizační tabulky nejsou standardem JPEG předepsány (resp. existuje už výše zmíněný návrh normovaných tabulek, avšak nemusí se dodržovat), pro každou aplikaci je tedy teoreticky možné zvolit tabulky vlastní, které například zachovávají vertikální hrany apod. Tabulky také mohou reflektovat fyzikální vlastnosti média, na které se obrázek pořizuje, například je možné předpokládat přítomnost „vypálených“ či naopak „přepálených“ pixelů u CCD čipů. Jedna z možných variant kvantizační tabulky je ukázána na šestém obrázku.

Za povšimnutí stojí, že se velikost koeficientů obecně zvyšuje spolu s rostoucím x-ovým i y-ovým indexem, tabulka však v tomto ohledu není zcela pravidelná. Například koeficient Q_7,7 v levém dolním rohu má nižší hodnotu (a tím i vyšší váhu) než jeho sousedé. Většina aplikací (včetně digitálních fotoaparátů) používá větší množství kvantizačních tabulek, protože je nutné pro různé faktory kvality q zvolit jiné hodnoty. Typicky bývají v aplikaci uloženy tři až čtyři kvantizační tabulky (někdy však i více než deset) a podle nastaveného faktoru kvality se mezi hodnotami v tabulkách provádí lineární interpolace.

Podívejme se nyní, jakým způsobem je možné kvantovací tabulky použít. Aplikace má například tři kvantovací tabulky, jednu pro q=10, druhou pro q=50 a třetí pro q=95 (hodnoty pod 10 a nad 95 většinou nemá v praxi cenu používat). Uživatel nastavil faktor kvality na hodnotu q=80. Aplikace nyní získá dvě nejbližší kvantizační tabulky, v tomto případě jsou to tabulky pro q=50 a q=95. Dále si aplikace pomocí běžné lineární interpolace vypočítá hodnoty nové kvantizační tabulky po q=80. Tato kvantizační tabulka je posléze použita pro kvantování DCT koeficientů se zadanou kvalitou. Zájemci o různé typy kvantizačních tabulek se mohou podívat na stránku http://www.im­pulseadventure­.com/photo/jpeg-quantization.html, na které jsou uvedeny odkazy na kvantizační tabulky použité v mnoha digitálních fotoaparátech a také několika konverzních programů.

Obrázek 6: Možná podoba kvantizační tabulky

5. Zpracování stejnosměrných složek (DC)

Před linearizací kvantovaných koeficientů se nad vypočtenými daty provádí ještě jedna operace, která má vést k výsledné redukci celkového počtu bitů. Od stejnosměrné složky (DC) se odečte hodnota stejnosměrné složky z předchozího bloku dat (tj. z bloku ležícího nalevo od zpracovávaného bloku popř. bloku ležícího na konci předchozích osmi obrazových řádků). Vzhledem k tomu, že v reálných obrázcích existují souvislé barevné plochy a DC složka odpovídá průměrnému jasu či barvě pixelů v daném bloku, vede tato operace k tomu, že nové hodnoty DC složek jsou poměrně nízké a tudíž se mohou zakódovat do menšího počtu bitů. U střídavých složek (AC) nemá tuto operaci cenu provádět, protože střídavé složky se v obrázku většinou neopakují. Tato operace by měla smysl pouze tehdy, pokud by se kódoval obrázek obsahující horizontální či vertikální hrany (popř. barevné přechody) se vzdáleností 8, 16, 24, 32… pixelů, to však zcela jistě není případ většiny obrázků ukládaných do JPEGu.

6. Linearizace kvantovaných koeficientů pomocí cik-cak sekvence

Při kvantizaci DCT koeficientů získáme v každém kroku zpracování matici 8×8 kvantovaných hodnot. Tyto hodnoty je nutné převést do lineární podoby, tj. do sekvence bitů. Také způsob linearizace použitý v JPEGu byl navržen tak, aby výsledkem byly co nejdelší sekvence nulových bitů, které je možné velmi efektivním způsobem zakódovat (zkomprimovat) buď pomocí Huffmanova kódování nebo kódování aritmetického. Účinné by bylo také LZ77 nebo LZW kódování, to však není v JPEGu použito. Ve skutečnosti není použitý způsob linearizace zcela optimální (u většího DCT bloku by bylo výhodnější linearizovat „po kružnicích“), ale pro tak malý blok, jako je 8×8 hodnot použitých v JPEGu jsou změny v cestě nepatrné, proto dali tvůrci přednost sekvenci jednoduše zapamatovatelné i implementova­telné. Sekvence postupného čtení hodnot kvantovaných koeficientů z matice je zobrazena na sedmém obrázku:

Obrázek 7: Sekvence postupného čtení hodnot kvantovaných koeficientů z matice N

7. Obsah dalšího pokračování tohoto seriálu

V následující části tohoto seriálu bude uveden postup Huffmanova kódování kvantovaných a následně linearizovaných DCT koeficientů. Také si popíšeme formát souborů JFIF (JPEG), ve kterém jsou uloženy hodnoty jednotlivých pixelů po jejich Huffmanovu či aritmetickém zakódování.