Obsah
1. Transformace barev z prostoru RGB do prostoru YCbCr
2. Praktický příklad transformace barev
3. Ukázky transformovaných obrázků
4. Podvzorkování barvonosných složek v barvovém prostoru YCbCr
5. Praktický příklad na podvzorkování barvonosných složek
6. Ukázky podvzorkovaných obrázků
7. Obsah dalšího pokračování tohoto seriálu
1. Transformace barev z prostoru RGB do prostoru YCbCr
V předchozí části tohoto seriálu jsme si řekli, že ve standardu JPEG jsou navrženy celkem čtyři režimy komprimace obrazových dat. Jedná se o sekvenční (ztrátový) režim, progresivní (také ztrátový) režim, bezeztrátový režim a konečně hierarchický (ztrátový) režim. V dalším textu jsme se podrobněji zabývali pouze sekvenčním režimem, ve kterém – aby vše nebylo příliš jednoduché a přímočaré – je možné použít celkem pět způsobů, jakými jsou obrazová data zpracovávána. Jednotlivé způsoby zpracování se od sebe liší především bitovou hloubkou barevných vzorků pixelů na vstupu (8 či 12 bitů na vzorek), způsobem výpočtu DCT spolu s kvantizací (základní a rozšířený režim) a konečně použitým kódováním kvantizovaných DCT koeficientů (aritmetické nebo Huffmanovo kódování).
V následujících kapitolách si podrobněji – včetně několika příkladů – popíšeme první dva kroky základního (baseline) způsobu zpracování, který by měly implementovat všechny kodéry i dekodéry JPEGu odpovídající této normě. U dekodérů je průběh zpracování obrazových dat samozřejmě opačný: od dekódování přes zpětnou DCT až po transformaci z prostoru YCbCr do barvového prostoru RGB. Na prvním obrázku, který obsahuje všech pět cest zpracování obrazových dat, je blok základního (baseline) zpracování rastrového obrazu zvýrazněn červenou barvou. Vidíme, že blok základního systému na svém vstupu očekává osmibitové barvové vzorky a výstup je kódován Huffmanovým kódem, který pro potřeby JPEGu používá vlastní slovníky bitových sekvencí. Některé části slovníků byly zjištěny statistickým rozborem mnoha obrázků.

Obrázek 1: Umístění bloku základního zpracování obrazových dat v řetězci sekvenčního (ztrátového) režimu
Minule jsme si také řekli, že rastrová data jsou před provedením navazujících operací převedena z barvového prostoru RGB, CMYK či interního barvového prostoru CCD čipu do barvového prostoru nazvaného YCbCr. Tato transformace mezi dvojicí barvových prostorů, která je vyznačena na druhém obrázku červenou barvou, je bezeztrátová, tj. nemůže při ní dojít k žádné ztrátě informací o obrázku, což si ostatně ukážeme na demonstračním příkladu popsaném v následující kapitole (jediná chyba může nastat vlivem zaokrouhlení nebo oříznutí výsledků, to je však spíše chyba implementace). Pokud tedy obrázek převedeme do barvového prostoru YCbCr, můžeme ho kdykoli převést zpátky do barvového prostoru RGB či CMYK a měli bychom dostat vždy výsledek identický s obrázkem původním.

Obrázek 2: Blok transformace barev do barvového prostoru YCbCr
Převod jednotlivých barvových složek R, G a B na složky Y, Cb a Cr se provádí podle následují trojice vzorců. Předpokladem pro úspěšný převod je, že všechny barvové složky jsou uloženy jako bezznaménkové celé číslo o délce minimálně osmi bitů (většinou se jedná o datový typ byte či unsigned char). Pro dvanáctibitovou hloubku barvových složek se ve vzorcích používají jiné aditivní a multiplikativní konstanty, v 99% případů si však vystačíme s osmibitovými vzorky.
Y = 0,299 R + 0,587 G + 0,114 B
Cb = - 0,1687 R - 0,3313 G + 0,5 B + 128
Cr = 0,5 R - 0,4187 G - 0,0813 B + 128 Zpětný přepočet (ten provádí dekodér umístěný například v prohlížečce obrázků či ve Webovém browseru) se provede pomocí vzorců:
R = Y + 1.402 (Cr-128)
G = Y - 0.34414 (Cb-128) - 0.71414 (Cr-128)
B = Y + 1.772 (Cb-128) Všechny výše uvedené vzorce budou použity ve dvou demonstračních příkladech, které jsou popsány v navazujících kapitolách.
2. Praktický příklad transformace barev
Na dnešním prvním demonstračním příkladu je ukázáno, jakým způsobem je možné provést převod plnobarevného obrázku (truecolor) z barvového prostoru RGB do barvového prostoru YCbCr. V obou barvových prostorech se používají osmibitové vzorky. Po překladu zdrojového kódu (zde je varianta se zvýrazněnou syntaxí) získáme program, který jako svůj jediný argument očekává jméno plnobarevného obrázku uloženého v nekomprimovaném formátu TGA (Targa, viz předchozí části tohoto seriálu). Posléze se program pokusí celý obrázek načíst do operační paměti a v případě úspěšného načtení je provedena konverze z barvového prostoru RGB, který je v TGA formátu implicitně používán, do barvového prostoru YCbCr, který je naopak použit v JPEGu.
Následně jsou vytvořeny tři další soubory typu TGA, ve kterých jsou uloženy obrázky ve stupních šedi (grayscale). První soubor (na konci svého jména má přidaný řetězec „_y“) obsahuje hodnotu složky Y, tj. signálu nesoucího informaci o světlosti pixelů bez ohledu na jejich barvu. Druhý obrázek s postfixem „_cb“ reprezentuje hodnoty rozdílové barvové složky Cb a konečně obrázek s postfixem „_cr“ hodnoty rozdílové barvové složky Cr. Čím vyšší jsou vypočtené hodnoty dané barvové složky, tím světlejší jsou pixely uložené ve výstupní trojici obrázků. Hodnota šedé (okolo 128) znamená, že se v obrázku nevyskytují rozdílové barvy Y-R a/nebo Y-B. Při pokusu o konverzi již „černobílého“ obrázku (ovšem uloženého jako truecolor!) by měl na výstupu vzniknout první obrázek odpovídající zdroji (složka Y odpovídá intenzitě) a další dva obrázky se všemi pixely nastavenými na konstantní hodnotu 128.
Převážná část funkcionality programu je soustředěna ve funkci nazvané rgb2ycbcr(), která má následující podobu (všimněte si, že vzorec pro přepočet barev je stejný jako první trojice vzorců uvedená v předchozí kapitole):
//-----------------------------------------------------------------------------
// Provedení transformace z barvového prostoru RGB do barvového prostoru YCbCr
//-----------------------------------------------------------------------------
void rgb2ycbcr(void)
{
int i, j;
for (j=0; j<src->height; j++) { // smyčka procházející všechny řádky zdrojové pixmapy
unsigned char *p_rgb=src->pixels+(3*j*src->width);
unsigned char *p_y= dest_y->pixels+(j*dest_y->width);
unsigned char *p_cb= dest_cb->pixels+(j*dest_cb->width);
unsigned char *p_cr= dest_cr->pixels+(j*dest_cr->width);
for (i=0; i<src->width; i++) { // smyčka procházející všechny pixely na obrazovém řádku
float r, g, b;
float y, cb, cr;
r=*p_rgb++; // získat barvové složky RGB
g=*p_rgb++;
b=*p_rgb++;
y = 0.299 *r+0.587 *g+0.114 *b; // provést přepočet z RGB na YCbCr
cb=-0.1687*r-0.3313*g+0.5 *b+128;
cr= 0.5 *r-0.4187*g-0.0813*b+128;
*p_y++=(unsigned char)y; // převod vypočtených hodnot na byty
*p_cb++=(unsigned char)cb; // a uložení do cílové pixmapy
*p_cr++=(unsigned char)cr;
}
}
}
//-----------------------------------------------------------------------------
3. Ukázky transformovaných obrázků
Ukažme si nyní výstupy z dnešního prvního demonstračního příkladu. Začneme – jak jinak – slavným obrázkem Lenny. Po transformaci do barvového prostoru YCbCr můžeme postřehnout, že nejvíce informací je umístěno v obrázku s hodnotami Y, zatímco další dva obrázky obsahují více šedivé barvy. Ještě lépe rozdíly mezi jednotlivými složkami vyniknou při zobrazení histogramu (například v GIMPu). Vysvětlení této disproporce je logické – původní obrázek opravdu obsahuje malé množství barev, resp. barvy nejsou v histogramu rozmístěny rovnoměrně. Pokud se např. v GIMPu pokusíme obrázek vyvážit, bude celá situace vypadat jinak. Ručně vyvážený obrázek je zobrazený na sedmém obrázku.

Obrázek 3: Původní obrázek Leny v barvovém prostoru RGB

Obrázek 4: Intenzita složky Y

Obrázek 5: Intenzita rozdílové barvové složky Cb

Obrázek 6: Intenzita rozdílové barvové složky Cr

Obrázek 7: Barevně vyvážený obrázek Lenny
Na následující čtveřici obrázků je zobrazen převod do barvového prostoru YCbCr pixmapy, která obsahuje screenshot části dialogu určeného pro výběr barvy ve známém grafickém editoru GIMP. Za povšimnutí stojí dvě zajímavosti. První je, že ikony v horní části obrázku (kromě ikony „duhového kola“) nesou velmi málo barvových informací, které jsou kódovány v kanálech Cb a Cr, proto také nejsou na obrázcích 10 a 11 tyto ikony prakticky viditelné. Druhá zajímavost je zobrazena na posledním (jedenáctém) obrázku. Trojúhelník s barevným přechodem totiž neobsahuje prakticky žádnou intenzitu červené barvové složky, proto na obrázku s intenzitou složky Cr téměř zmizel. Při korektně nastavené „rotaci“ trojúhelníku tak, aby jeho vrchol mířil na čistě modrou barvu, by tento trojúhelník neměl být viditelný vůbec.

Obrázek 8: Část dialogu pro výběr barvy v GIMPu
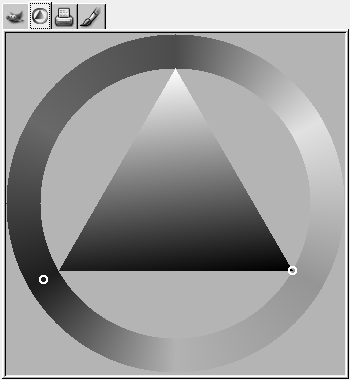
Obrázek 9: Intenzita složky Y

Obrázek 10: Intenzita rozdílové barvové složky Cb

Obrázek 11: Intenzita rozdílové barvové složky Cr
Na dalších čtveřici obrázků si všimněte, že v dialogu, ve kterém by se teoreticky měly vyskytovat pouze barvy se stejnou intenzitou, se po jeho převedení na složku Y přece jen patrné rozdíly v intenzitě barev objevují. Je to způsobeno zejména jinými přepočítacími koeficienty mezi složkami RGB a složkou Y (luminance) u systému YCbCr popř. složkou L (lightness) u systému HLS či složkou V (value) u systému HSV. Mimochodem – skrolovací lišta na pravé straně screenshotu je šedá, proto není na obrázcích 14 a 15 vůbec viditelná.

Obrázek 12: Jiná část dialogu pro výběr barvy v GIMPu

Obrázek 13: Intenzita složky Y

Obrázek 14: Intenzita rozdílové barvové složky Cb

Obrázek 15: Intenzita rozdílové barvové složky Cr
V systémech Microsoft Windows nabízí WinAPI také dialog pro výběr barvy. Při bližším pohledu na rozmístění barev je patrné, že se jedná o rozvinutý jehlan modelu HSV, což je také patrné ze šestnáctého obrázku.

Obrázek 16: Dialog pro výběr barvy, který nabízí knihovny WinAPI
4. Podvzorkování barvonosných složek v barvovém prostoru YCbCr
Dalším krokem zpracování obrazových dat je redukce neboli podvzorkování barvonosných složek. Ideu podvzorkování jsme si přiblížili minule: vzhledem k menší citlivosti lidského oka na odstíny barev než na intenzitu světla jsou barvonosné složky Cb a Cr ukládány v menším rastru než složka Y, která obsahuje intenzitu jednotlivých pixelů. Tento způsob ztrátové transformace není pouze doménou JPEGu, jak by se mohlo na první pohled zdát. Například všechny normy analogového barevného televizního vysílání (SECAM, PAL, NTSC) podobnou funkci už v principu své práce obsahují, i když v analogové podobě. Digitální televize používá prakticky stejný způsob jako JPEG, což však není nic překvapivého, protože HDTV z JPEGu vlastně vychází.
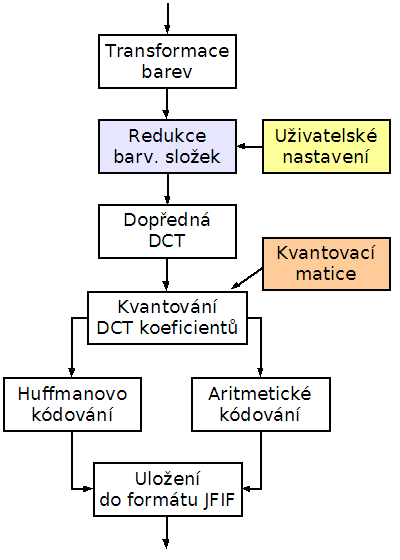
Obrázek 17: Blok redukce (podvzorkování) barvonosných složek
Podvzorkování barvonosných složek je v JPEGu možné provádět dvěma způsoby. Buď jsou vypočteny barvové poměry dvou pixelů, které spolu sousedí na jednom obrazovém řádku, nebo se vypočte průměr barev čtyř sousedních pixelů (ty leží na dvou obrazových řádcích). Při výpočtu průměru barev ze dvou sousedních pixelů dochází ke zmenšení objemu rastrových dat (pro tyto dva pixely) ze 6 bytů na 4 byty, tj. na cca 66%. Větší úspory objemu se dosáhne při použití čtyř pixelů tvořících informaci o barvě, kde se původních 12 bytů sníží na 6 bytů, tj. na 50%. Tyto hodnoty vypadají velmi zajímavě: prakticky bez větší práce jsme provedli komprimaci o jednu třetinu či dokonce o jednu polovinu celkového objemu. Jak se však tato ztráta informace projeví na obrázcích? To je téma následující kapitoly.
5. Praktický příklad na podvzorkování barvonosných složek
V dnešním druhém demonstračním příkladu, jehož zdrojový kód je umístěný zde (HTML verze se zvýrazněnou syntaxí), je ukázáno, jakým způsobem je možné provádět podvzorkování barvonosných složek Cb a Cr. Podvzorkování je záměrně prováděno tím nejhrubším způsobem, při kterém se bere v úvahu pouze barva jednoho pixelu v bloku a barvy ostatních pixelů se ignorují. Ve skutečnosti se v JPEGu provádí průměrování barev sousedních pixelů, což vede k vizuálně více kvalitním výsledkům. Program také umožňuje změnu velikosti bloku, ve kterém se provádí podvzorkování. JPEG má bloky velikosti 2×1 pixel, popř. 2×2 pixely, v programu lze nastavit čtvercový blok o libovolné velikosti (význam však mají bloky, jejichž šířka a výška je celočíselnou mocninou čísla 2).
Program při svém spuštění vyžaduje jeden parametr, což je jméno plnobarevného obrázku uloženého v nekomprimovaném formátu TGA (Targa). Následně je proveden přepočet do barvového prostoru YCbCr, podvzorkování barev a zpětný převod do prostoru RGB. Výsledkem jsou dva soubory typu TGA – jeden obsahující ztrátově transformovaný původní obrázek a druhý soubor obsahující rozdílový obrázek, přičemž jednotlivé rozdíly (vlastně chyby vzniklé ztrátovou transformací) jsou vynásobeny deseti, jinak by nebyly patrné. Funkce, která provádí transformaci, podvzorkování barvových složek a zpětnou transformaci do barvového prostoru RGB, vypadá následovně:
//-----------------------------------------------------------------------------
// Provedení transformace z barvového prostoru RGB do barvového prostoru YCbCr
// s redukcí barvonosných složek Cb a Cr podle nastavení konstanty BLOCK
//-----------------------------------------------------------------------------
void reduce_colors(void)
{
#define BLOCK 1
//memcpy(dest->pixels, src->pixels, src->width*src->height*3);
int i, j;
for (j=0; j<src->height; j++) { // pro všechny řádky zdrojové pixmapy
unsigned char *p_dest=dest->pixels+(3*j*dest->width);
for (i=0; i<src->width; i++) { // pro všechny pixely na řádku
float r, g, b, rr, gg, bb;
float y, cb, cr;
// souřadnice zarovnané na začátek bloku
int ii=i & (~BLOCK);
int jj=j & (~BLOCK);
// barvové složky pro každý pixel
r=getR(i, j);
g=getG(i, j);
b=getB(i, j);
// barvové složky platné pro celý blok
rr=getR(ii, jj);
gg=getG(ii, jj);
bb=getB(ii, jj);
// provést přepočet z prostoru RGB
y = 0.299 *r+0.587 *g+0.114 *b;
cb=-0.1687*rr-0.3313*gg+0.5 *bb+128;
cr= 0.5 *rr-0.4187*gg-0.0813*bb+128;
// zpětný přepočet do prostoru RGB
r=y +1.402 *(cr-128);
g=y-0.34414*(cb-128)-0.71414*(cr-128);
b=y+1.772 *(cb-128);
// zkontrolovat meze
// (může nastat přetečení)
if (r>255) r=255;
if (g>255) g=255;
if (b>255) b=255;
if (r<0) r=0;
if (g<0) g=0;
if (b<0) b=0;
*p_dest++=(unsigned char)r; // převod na byty a uložení
*p_dest++=(unsigned char)g;
*p_dest++=(unsigned char)b;
}
}
}
//-----------------------------------------------------------------------------
6. Ukázky podvzorkovaných obrázků
Následující šestice obrázků nám ukazuje, jak se vizuálně projeví ztráta informace způsobená redukcí barvonosných složek. Na první pohled není mezi obrázky rozdíl, při přiblížení však můžeme pozorovat nepatrné chyby, například v oblasti nosu nebo klobouku. Rozdílové obrázky nám chyby zvýrazní, ovšem musíme mít na paměti, že se jedná o hodnoty vynásobené deseti – bez tohoto násobení by byl rozdílový obrázek prakticky černý. Rozhodnutí, jak velký blok se má pro podvzorkování při komprimaci pomocí JPEGu zvolit, již ponechám na čtenáři, osobně však vždy nastavuji 2×2 pixely (většina zařízení však toto nastavení provádí automaticky).

Obrázek 18: Původní obrázek Lenny

Obrázek 19: Podvzorkování barvonosných složek v bloku 2×2 pixely

Obrázek 20: Rozdílový obrázek

Obrázek 21: Podvzorkování barvonosných složek v bloku 4×4 pixely

Obrázek 22: Rozdílový obrázek
7. Obsah dalšího pokračování tohoto seriálu
V dnešní části seriálu již nemáme prostor pro vysvětlení výpočtu dopředné i inverzní diskrétní kosinové transformace spolu s kvantováním DCT koeficientů pomocí kvantizačních tabulek. Proto si toto zajímavé téma ponecháme až na další díl.





































